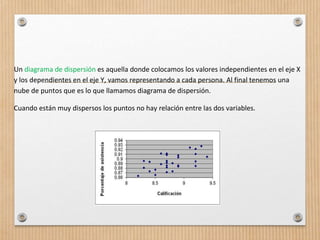
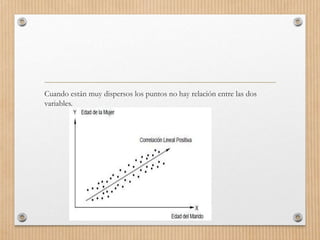
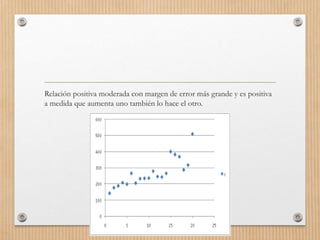
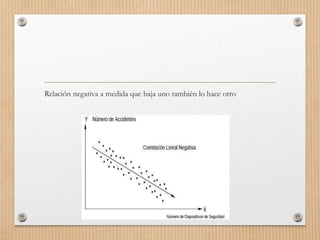
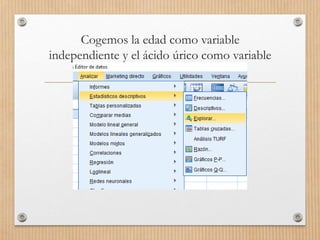
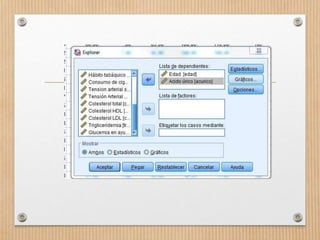
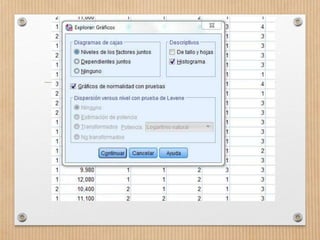
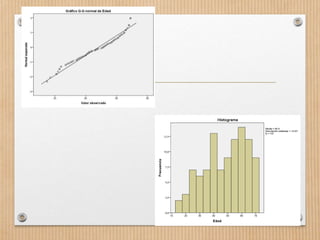
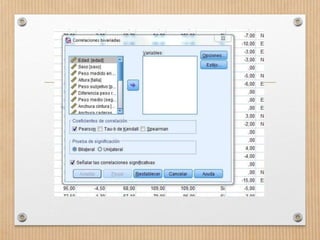
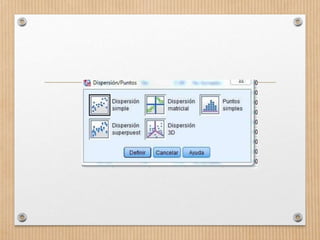
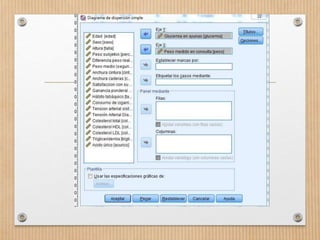
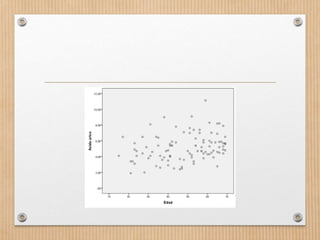
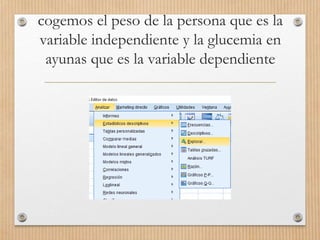
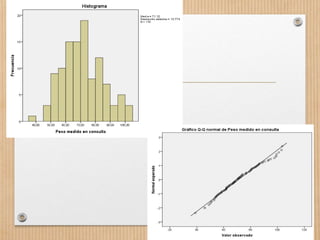
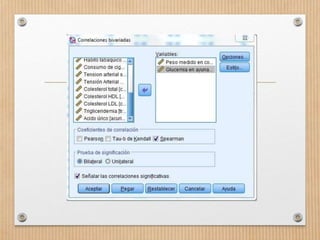
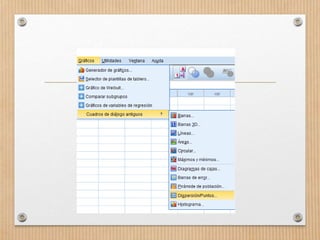
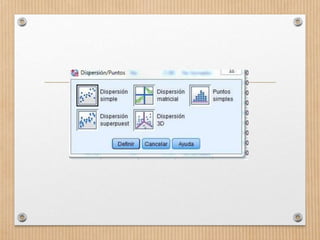
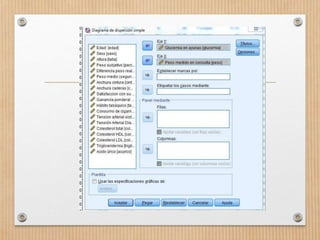
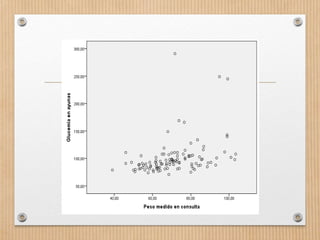
Este documento describe los conceptos de concordancia y correlación bivariada. Explica que la correlación mide la relación entre dos variables, ya sea positiva si aumentan juntas o negativa si una aumenta mientras la otra disminuye. También presenta los coeficientes de correlación de Pearson y Spearman, y cómo realizar pruebas de normalidad y correlación para determinar si existe una relación estadísticamente significativa entre dos variables. Finalmente, incluye un ejemplo numérico para ilustrar el proceso.

1. Concordancia y
correlación

2. Concordancia bivariada
Hipótesis en las que las dos variables son variables numéricas en el momento que alguna de
las dos no es cuantitativa ya no lo podemos utilizar. Es bivariada ya que hay dos variables una
dependiente y otra independiente. Ejemplo: talla y edad, donde la edad influye en la talla.
Existe correlación entre dos variables si estas varían conjuntamente.
: si el cambio es en la misma dirección. Al aumentar la edad,-Correlación positiva
aumenta la talla.
: si el cambio se produce en distinta dirección. Niveles-Correlación negativa
plasmáticos que disminuyen con la edad.

3. Un diagrama de dispersión es aquella donde colocamos los valores independientes en el eje X
y los dependientes en el eje Y, vamos representando a cada persona. Al final tenemos una
nube de puntos que es lo que llamamos diagrama de dispersión.
Cuando están muy dispersos los puntos no hay relación entre las dos variables.

4. Cuando están muy dispersos los puntos no hay relación entre las dos
variables.

5. Relación positiva moderada con margen de error más grande y es positiva
a medida que aumenta uno también lo hace el otro.

6. Relación negativa a medida que baja uno también lo hace otro

7. Coeficientes de correlaciónR de Pearson
-Estadístico de elección, el más utilizado, si las variables se distribuyen normalmente
Valores
entre -1
y 1
0 no hay
correlación
1 es
correlación
positiva
-1 es
correlación
negativa

8. Rho de Sperman
Si las variables no se distribuyen normalmente
• -Si 0,05>p; rechazamos la hipótesis nula  hay correlación
• -Antes de hacer la prueba de correlación debemos realizar la
prueba de normalidad, donde utilizamos la prueba de
kolmogorov- smirnov si el tamaño de la muestra es superior a
50, y shapiro wilks menos a 50.

9. Datos importantes
• P(sig)>0,05 HAY NORMALIDAD
• P(sig)<0,05 NO HAY NORMALIDAD
• P(sig)>0,05 si hay correlación
• P(sig)<0,05 no hay correlación

10. EJERCICIO 1
Debemos coger dos posibles correlaciones pero la
justificamos, le hacemos la prueba de normalidad para
cada una, al comprobar la normalidad hacemos la
correlación, comentamos los resultados y
representamos gráficos.

11. Cogemos la edad como variable
independiente y el ácido úrico como variable
dependiente

14. Ninguna de las dos siguen la normalidad ya
que sig es menos que 0,05
Pruebas de normalidad
1.
Kolmogorov-Smirnova
Shapiro-Wilk
Estadístico gl Sig. Estadístico gl Sig.
Edad ,095 101 ,024 ,945 101 ,000
Acido úrico ,084 101 ,077 ,972 101 ,031

16. Entonces debemos utilizar spearman
al no seguir la normalidad

18. Entonces miramos que sig es 0,001 entonces
si hay correlación y al ser 0,312 entonces es
correlación positiva.
Correlaciones
Edad Acido úrico
Rho de Spearman Edad Coeficiente de correlación 1,000 ,312**
Sig. (bilateral) . ,001
N 240 101
Acido úrico Coeficiente de correlación ,312**
1,000
Sig. (bilateral) ,001 .
N 101 101

19. Hacemos las gráficas

23. EJERCICIO 2
Debemos coger dos posibles correlaciones pero la
justificamos, le hacemos la prueba de normalidad para
cada una, al comprobar la normalidad hacemos la
correlación, comentamos los resultados y
representamos gráficos.

24. cogemos el peso de la persona que es la
variable independiente y la glucemia en
ayunas que es la variable dependiente

26. Calculamos la normalidad y obtenemos que
ambas no siguen la normalidad entonces no
hay normalidad y elegimos spearman
Pruebas de normalidad
Kolmogorov-Smirnova Shapiro-Wilk
Estadístico gl Sig. Estadístico gl Sig.
Peso medido en consulta
,072 110 ,200* ,985 110 ,237
Glucemia en ayunas
,242 110 ,000 ,595 110 ,000

28. Hacemos la correlación con
Spearman

30. Entonces 0,485 entonces hay correlación y
positiva y p(0)<0,05 entonces si hay
correlación
Correlaciones
Peso medido en
consulta
Glucemia en
ayunas
Rho de Spearman Peso medido en consulta Coeficiente de correlación 1,000 ,485**
Sig. (bilateral) . ,000
N 240 110
Glucemia en ayunas Coeficiente de correlación ,485** 1,000
Sig. (bilateral) ,000 .
N 110 110

31. Hacemos los gráficos