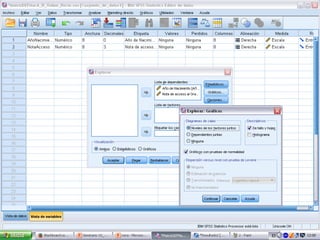
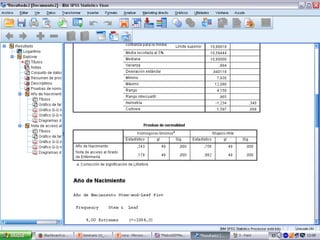
Este documento presenta el análisis de correlación entre dos variables cuantitativas, el año de nacimiento y la nota de acceso, de un cuestionario. Se realizan las pruebas de normalidad de ambas variables y se determina que no siguen una distribución normal, por lo que se utiliza el estadístico de Spearman. Los resultados muestran que no existe correlación entre las dos variables.

1. Nora Mª Mijes Montes
1º Enfermería Macarena. Grupo A/subgrupo 3

2. Tarea
 Elige dos variables de la matriz de datos del
cuestionario.
 La que queráis pero deberás justificarla.
 Recuerda que tienes que hacer la prueba de
normalidad para decidir el estadístico de
correlación que tienes que utilizar.
 Comenta los resultados.
 Represéntalos gráficamente.

4. Trabajo
 He escogido las variables año de nacimiento y la
nota de acceso porque son variables cuantitativas.
Con dos variables cuantitativas puedo estudiar la
correlación que hay entre ellas.
 Para estudiar la correlación entre ellas se debe
realizar:
 La prueba de normalidad de las dos variables.
 Comprobar si hay correlación entre ellas.
 Hacer el gráfico para visualizarlo mejor.

5. Trabajo
 Para hacer la prueba de la normalidad, en el SPSS
le damos a “Analizar”, “Estadísticos descriptivos” y
“Explorar”.
 En el cuadro siguiente añadimos las dos variables,
le damos a “Gráficos” y en el siguiente recuadro
picamos la opción de “gráficos con pruebas de
normalidad”.

9. Trabajo
 Escogemos o la opción de “Shapiro” o la de
“Kolmogorov” ya que tengo dos variables con 50
sujetos y lo que hace distinguir una de otra es que
tenga mas o menos de 50 sujetos, por lo que da
igual cual escoger.
 Nos fijamos en la tabla en el apartado de “Sig” y
vemos que los valores de las dos variables son de
0,00.

10. Trabajo
 A continuación debemos comparar los valores de
Sig de las dos variables (independientemente una
de la otra) con el nivel de significación que es de
0,05.
 Vemos que 0,00<0,05 (año de nacimiento) y
0,00<0,05 (nota acceso) por lo que ninguna de las
dos sigue una distribución normal. Se rechaza la
hipótesis nula de que sigue una distribución
normal.

11. Trabajo
 Como ninguna de las dos sigue una distribución
normal, para realizar la correlación entre ellas
debemos utilizar el estadístico de Spearman.
 Para realizar los estadísticos de Spearman
debemos darle en el SPSS a “Analizar”,
“Correlaciones” y “Bivariables”. En el siguiente
recuadro metemos las variables y picamos la
opción de “Spearman”. Luego le damos a “Aceptar”.

15. Trabajo
 Vemos la tabla que nos ha salido, y nos fijamos en
el primer valor que hay cuando se cruzan las dos
variables (0,232). Vemos que no hay ningún
asterisco en el lado derecho, con lo que nos está
indicando que no hay correlación entre las dos
variables.
 Si hubiese correlación habría uno o dos asteriscos
según la intensidad de la correlación.

16. Trabajo
 Para realizar el grafico debemos, en el SPSS, darle a
“Gráficos”, “Cuadro de diálogos antiguos” y
“Dispersión/Puntos”. Le damos a distribución
simple.
 En el siguiente recuadro debemos elegir la variable
que se situará en el eje de las X y en el eje de las Y.
Luego de damos a “Aceptar”.
 Cuando te sale el gráfico se ve claramente que no
hay correlación entre ambas ya que forma ninguna
línea.