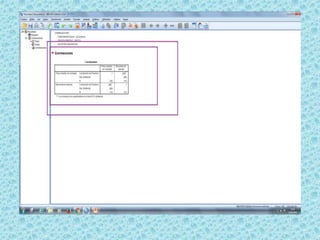
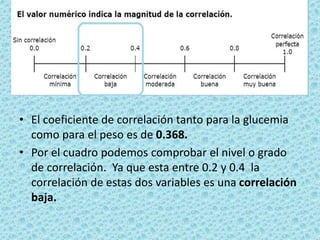
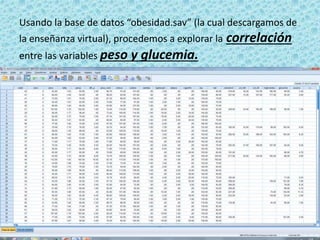
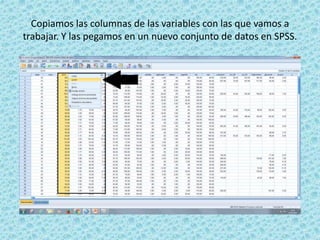
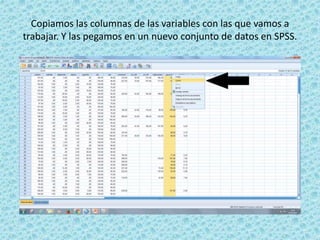
Este documento resume un seminario sobre correlación. Explora la correlación entre el peso y la glucemia usando datos de obesidad. Realiza pruebas de normalidad para ambas variables y determina que no siguen una distribución normal. Por lo tanto, usa el coeficiente de correlación de Spearman, una prueba no paramétrica. Los resultados muestran una correlación baja positiva de 0.368 entre el peso y la glucemia.







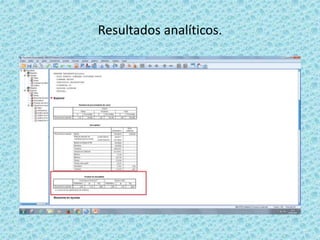

![• El siguiente paso es fijarnos en el nivel de significación y compararlo con el
nuestro ya preestablecido (0.5) (p valor)
A partir de esta comparación, podremos elegir entre H0 u H1.
• Como 0,0 < 0,5 rechazamos H0 y por consiguiente aceptamos H1. [conforme
este el nivel de significación mas cerca de cero, mas evidencia en contra de la
hipótesis nula (H0)]
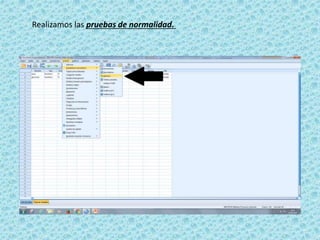
• H1: los datos NO siguen una distribución normal.](https://image.slidesharecdn.com/seminario9-160602155431/85/Seminario-9-20-320.jpg)
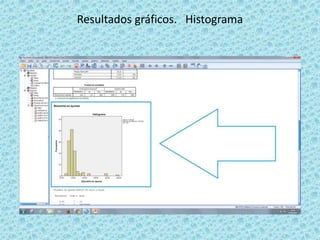




![• El siguiente paso es fijarnos en el nivel de significación y
compararlo con el nuestro ya preestablecido (0.5) (p valor)
A partir de esta comparación, podremos elegir entre H0 u H1.
Como 0,0 < 0,5 rechazamos H0 y por consiguiente aceptamos H1.
[conforme este el nivel de significación mas cerca de cero, mas evidencia en
contra de la hipótesis nula (H0)]
H1: los datos NO siguen una distribución normal.](https://image.slidesharecdn.com/seminario9-160602155431/85/Seminario-9-31-320.jpg)