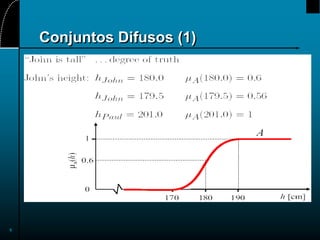
Este documento describe los conceptos básicos de los conjuntos difusos y su aplicación en sistemas inteligentes. Los conjuntos difusos fueron propuestos por Lotfi A. Zadeh en 1965 y permiten representar conceptos vagos mediante funciones de pertenencia que asignan un grado de pertenencia a cada elemento de un universo. Las operaciones con conjuntos difusos como la unión, intersección y complemento se definen generalizando los conceptos de la lógica clásica. Estos conjuntos se han aplicado exitosamente en diversas áreas como






















![27
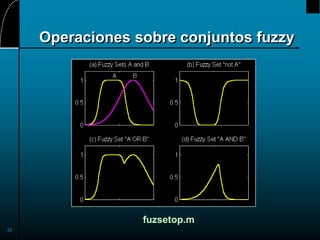
Convexidad de los conjuntos fuzzy
Un conjunto fuzzy A es convexo si para
cualquier l en [0, 1],
l l
A A A
x x x x
( ( ) ) min( ( ), ( ))
1 2 1 2
1
convexmf.m](https://image.slidesharecdn.com/unidad1a-230125070044-0755fe9b/85/Conjuntos-Difusos-ppt-27-320.jpg)




























![65
Algunos operadores generalizados
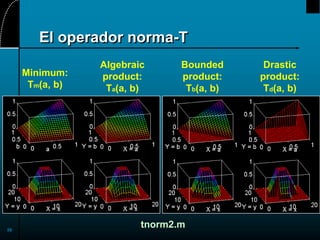
Norma-t
Conorma-t rango autor
Schweizer &Sklar [69]
1 max 0, (1 a) p
(1 b) p
1
1
p
max 0, a p
b p
1
1
p p (,)
a b (2 )ab
a (1 )ab
ab
(1 )(a b ab)
(0,) Hamacher [70]
min 1,(aw
bw
)
1
w
1 min 1,((1 a)w
(1 b)w
)
1
w
w (0,) Yager [72]
1
1
1
a
1
l
1
b
1
l
1
l
1
1
1
a
1
l
1
b
1
l
1
l
l (0,) Dombi [74]](https://image.slidesharecdn.com/unidad1a-230125070044-0755fe9b/85/Conjuntos-Difusos-ppt-65-320.jpg)

