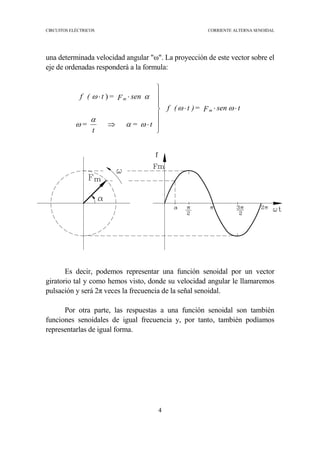
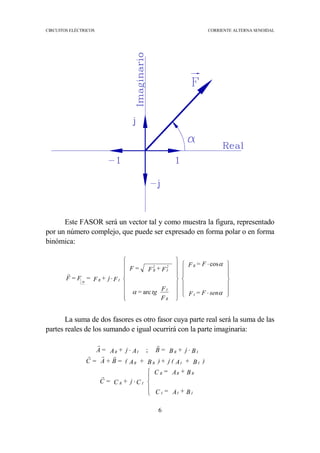
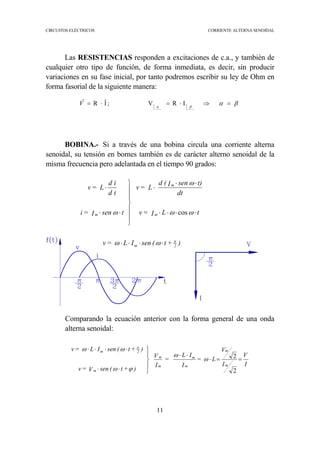
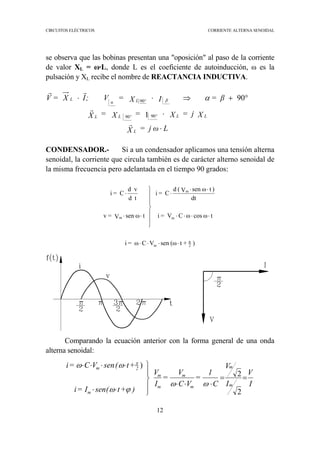
La corriente alterna senoidal es predominantemente utilizada en la producción y uso de energía eléctrica debido a su eficiencia y menor costo en comparación con corrientes continuas. Se describe cómo las alteraciones en circuitos con excitaciones senoidales producen respuestas senoidales, y se introduce el concepto de fasores para simplificar cálculos. Además, se detalla el comportamiento de resistencias, bobinas y condensadores en circuitos de corriente alterna senoidal y la importancia de la impedancia en este contexto.

![CIRCUITOS ELÉCTRICOS CORRIENTE ALTERNA SENOIDAL
3
2
F=F
m
ef
El valor eficaz de una función senoidal es el mas representativo pues
su valor medio hemos visto que es cero y además este valor eficaz representa
un valor de la función tal, que produce los mismos efectos caloríficos sobre
una resistencia que el mismo valor en corriente continua constante.
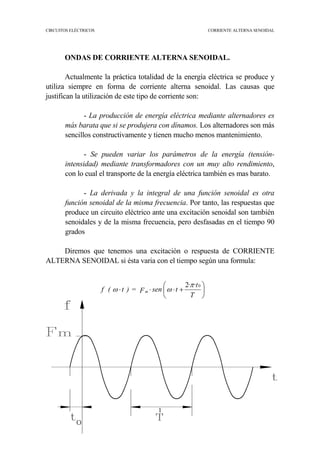
La aplicación a un circuito de excitaciones de corriente alterna senoidal
da lugar a respuestas que para calcularlas se deben utilizar ecuaciones con
integrales y derivadas de difícil solución.
Para facilitar estas soluciones se utiliza el concepto de fasor.
Imaginemos que tenemos un vector de módulo constante "Fm" y que gira a
( ) ( )[ ]
2
F
2
4
F
1-1-0-2
4
F
dtt2cos-dt
4
F
dt
2
t2cos-1
2
)(
2
1
)(
T
1
m
2
m
2
m
2
0
2
0
2
m
2
0
2
2
0
22
0
2
=⋅
⋅
=⋅⋅
⋅
=
=
⋅⋅⋅⋅
⋅
=⋅
⋅⋅
⋅
⋅
=
=⋅⋅⋅⋅
⋅
=⋅⋅=
∫ ∫∫
∫∫
π
π
π
π
ω
π
ω
π
ω
π
π ππ
π
m
m
T
ef
F
dttsenFdttfF
W16=IR=P
1=R
A.4=
2
24
=I
tsen24=)t(i
2
efef ⋅
Ω
⋅
⋅⋅⋅⋅ ωω](https://image.slidesharecdn.com/2-corrientealterna-180418104159/85/Corriente-Alterna-3-320.jpg)