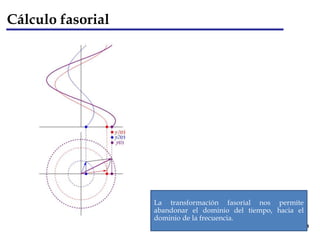
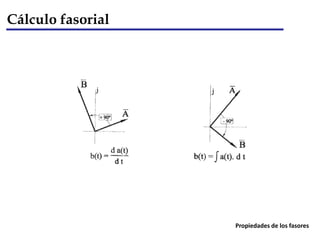
Este documento presenta los conceptos fundamentales del análisis de circuitos de corriente alterna utilizando el cálculo fasorial. Introduce la transformación fasorial para representar magnitudes senoidales en el dominio de la frecuencia mediante vectores complejos. Explica las propiedades de los fasores y cómo se aplican a elementos como resistores, bobinas y capacitores. Finalmente, muestra un ejemplo de resolución de circuito de CA usando el enfoque fasorial.

1. TEORÍA DE CIRCUITOS
SEMANA 6
Jorge Luis Jaramillo
TIETUTPL septiembre 2016

2. Créditos
Esta presentación fue preparada estrictamente como material de apoyo a la jornada presencial
del curso de Teoría de Circuitos, del programa de Ingeniería en Electrónica y
Telecomunicaciones que se imparte en el Universidad Técnica Particular de Loja.
La secuencia de contenidos corresponde al plan docente de la asignatura, y, para la elaboración
se han utilizado aportes propios del docente, y, una serie de materiales y recursos disponibles
gratuitamente en la web.

3. Corriente alterna
• Cálculo fasorial
• Impedancia
• Resolución de circuitos de CA utilizando fasores
• Discusión y análisis

4. Corriente alterna
•Cálculo fasorial

5. La resolución de circuitos de CA supone una dificultad adicional respecto de los
circuitos de CC. Desde esta perspectiva se busca diferentes procedimientos matemáticos
que eliminen o aminoren dicha dificultad. Uno de estos procedimientos es el
denominado de transformación fasorial al dominio de la frecuencia.
El análisis de las relaciones entre tensiones e intensidades senoidales en diferentes
circuitos, muestran que estas magnitudes tienen la misma frecuencia y por tanto la
misma pulsación. Esto supone que, en un circuito cualquiera con fuentes de CA de igual
frecuencia, todas las funciones instantáneas de dicho circuito pueden ser definidas
completamente por medio de dos y sólo dos parámetros: el valor eficaz y el ángulo
inicial.
Estos dos parámetros se prestan a ser representados matemáticamente por un único
elemento vectorial bidimensional, que por su propia naturaleza se representa por un
número complejo en forma polar.
Cálculo fasorial
Introducción

6. Al número complejo requerido se lo denomina con el anglicismo fasor, que es
la imagen paramétrica de una función senoidal cuya expresión instantánea se
recompone según la expresión y que es exclusivo
para la frecuencia de funcionamiento y sólo para ella.
Por otra parte, de acuerdo a la ecuación de Euler se cumple que ejωt = cosωt +
jsenωt, por lo que cualquier función senoidal puede representarse como fs(t) =
FSmejωt
Cálculo fasorial
Introducción

7. Cálculo fasorial
Introducción
La transformación fasorial nos permite
abandonar el dominio del tiempo, hacia el
dominio de la frecuencia.

8. El fasor 𝐶 de la función senoidal c(t), resultante de la suma o resta de otras 2 funciones
senoidales de igual frecuencia, a(t) y b(t), cuyos fasores son respectivamente 𝐴 y 𝐵,
coincide con la suma o resta de los 2 citados fasores.
El fasor 𝐵 de la función b(t), resultante de derivar respecto al tiempo la función
primitiva a(t), resulta ser el producto del número complejo del fasor de la función
primitiva por la cantidad imaginaria jω.
El fasor 𝐵 de la función b(t), resultante de integrar en el tiempo la función primitiva a(t),
es el cociente entre número complejo del fasor de la función primitiva y el número
complejo jω .
El fasor 𝐵 de la función b(t), resultante de multiplicar la función a(t) por un valor
constante escalar K, resulta ser el producto del fasor 𝐴 por dicha constante.
Cálculo fasorial
Propiedades de los fasores

9. Cálculo fasorial
Propiedades de los fasores

10. De acuerdo a la Ley de Ohm, en el
circuito se cumple que v(t) = Ri(t), lo que,
expresado en magnitudes complejas,
equivale a:
𝑉𝑝 𝑒 𝑗(ψ 𝑣) =R𝐼 𝑝 𝑒 𝑗(ψ 𝑖)
Cálculo fasorial
Tratamiento fasorial de elementos de circuitos: resistor
Se puede afirmar que ψ 𝑣= ψ𝑖 , lo que
significa que la corriente y el voltaje están
en fase

11. En una bobina se cumple que 𝑣 𝑡 = 𝐿 𝑑𝑖(𝑡)
𝑑𝑡
lo que expresado en magnitudes
complejas, equivale a:
𝑉𝑝 𝑒 𝑗(ψ 𝑣) = jω𝐿𝐼 𝑝 𝑒 𝑗(ψ 𝑖)
O bien: 𝑉𝑝 𝑒 𝑗(ψ 𝑣) = ω𝐿𝐼 𝑝 𝑒 𝑗(ψ 𝑖+90°)
Se puede afirmar que ψ 𝑣= ψ𝑖+ 90°, lo que
significa que la corriente y el voltaje están
fuera de fase en 90º. Se dice que el
voltaje adelanta a la corriente en 90º, o,
que la corriente esta atrasada respecto al
voltaje.
Cálculo fasorial
Tratamiento fasorial de elementos de circuitos: bobina

12. Cálculo fasorial
Tratamiento fasorial de elementos de circuitos: capacitor
En el capacitor se cumple que 𝑖 𝑡 = 𝐶
𝑑𝑉/𝑡)
𝑑𝑡
, lo que
expresado en magnitudes complejas equivale a:
𝐼 𝑝 𝑒 𝑗(ψ 𝑖) = jω𝐶𝑈 𝑝 𝑒 𝑗(ψ 𝑢)
Que también puede ser representado como:
𝐼 𝑝 𝑒 𝑗(ψ 𝑖) = ω𝐶𝑈 𝑝 𝑒 𝑗(ψ 𝑢+90°)
Se puede afirmar entonces que ψ𝑖= ψ 𝑢+ 90°, lo
que significa que la corriente y el voltaje están
fuera de fase en 90º. Se dice que la corriente
adelanta al voltaje en 90º, o, que el voltaje esta
atrasado de la corriente en 90º.

13. Cálculo fasorial
Tratamiento fasorial de elementos de circuitos: resumen

14. Corriente alterna
• Impedancia

15. La impedancia se define como la razón entre el voltaje fasorial y la corriente
fasorial, y, se simboliza con la letra Z.
La impedancia es una cantidad compleja cuya dimensión esta dada en ohm. La
impedancia no es un fasor
Un inductor se representa en el dominio del tiempo por su inductancia L, y, en el
dominio de la frecuencia por su impedancia jωL.
Un capacitor tiene una capacitancia C en el dominio del tiempo, y, una impedancia
1/jωc en el dominio de la frecuencia
Las impendancias se tratan como resistencias, pero sin olvidar que son magnitudes
complejas.
Impedancia
Impedancia

16. Corriente alterna
• Resolución de circuitos de CA utilizando fasores

17. Resolver el siguiente circuito:
Resolución de circuitos de CA utilizando fasores
Imagen tomada del sitio web de la
Biblioteca de la Universidad de la Rioja

18. Resolución de circuitos de CA utilizando fasores
Imagen tomada del sitio web de la
Biblioteca de la Universidad de la Rioja
AC
)(ti
k5.1 k1
F
6
1
Vtsen )3000(40
H
3
1
Resolver el siguiente circuito:

19. DISCUSIÓN Y ANÁLISIS