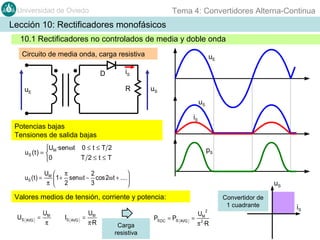
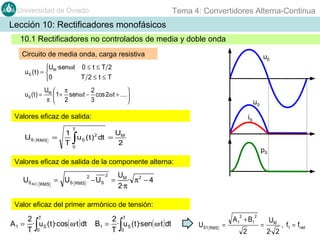
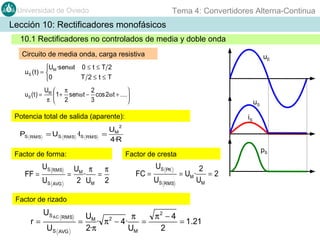
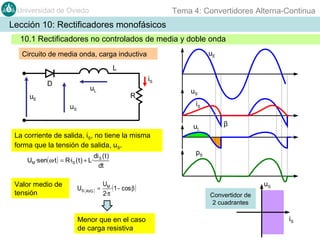
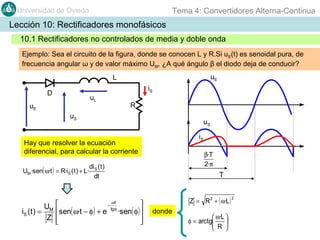
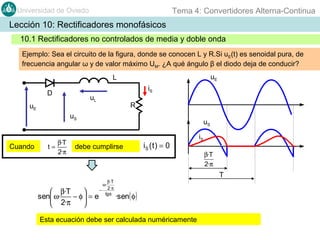
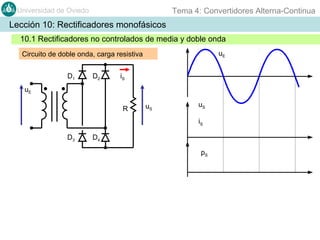
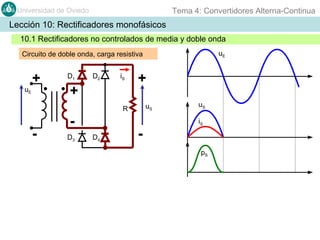
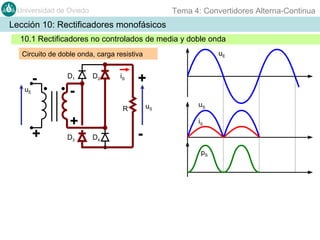
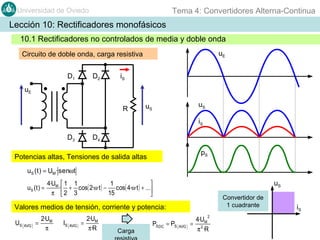
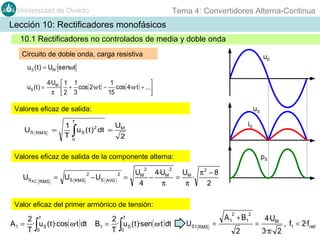
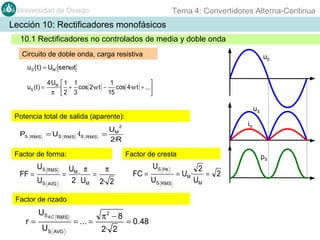
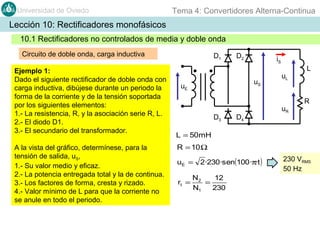
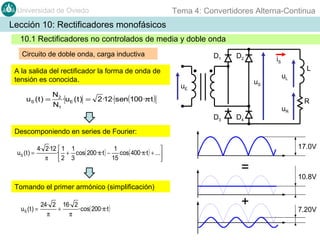
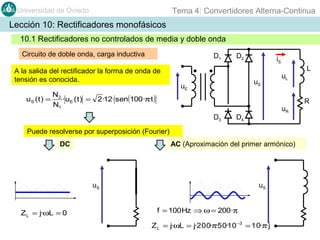
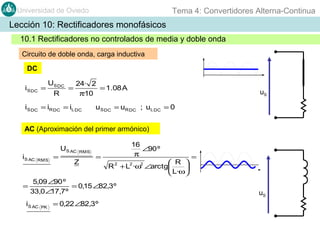
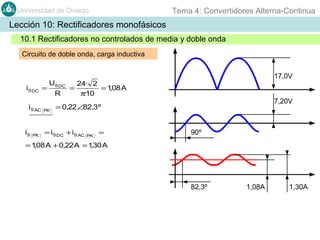
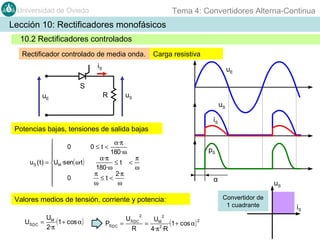
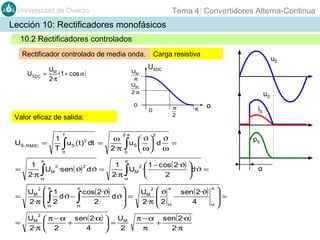
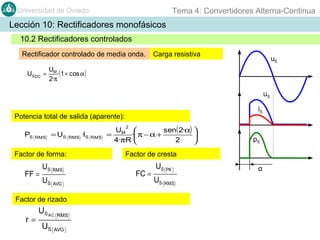
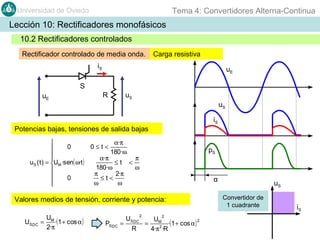
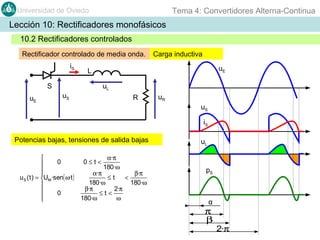
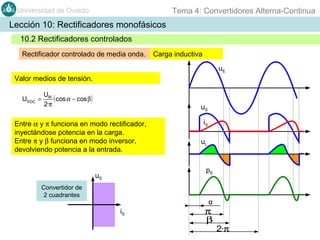
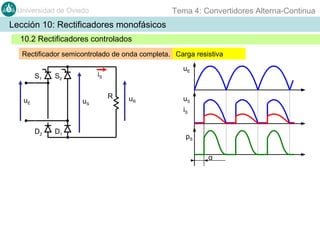
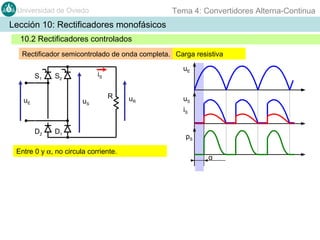
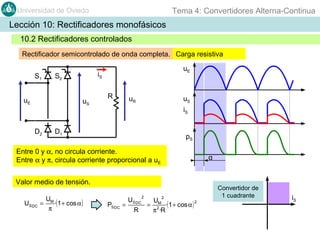
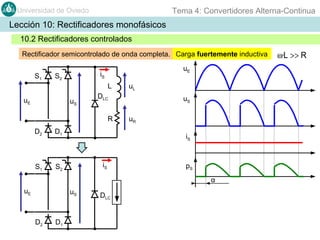
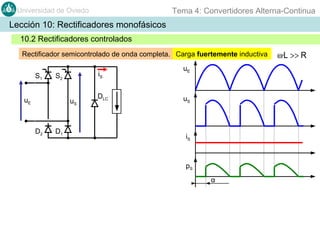
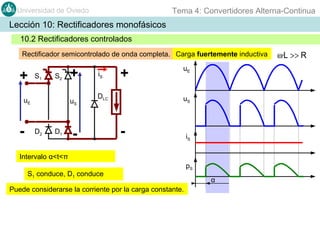
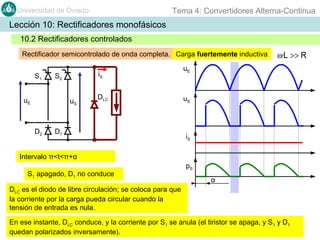
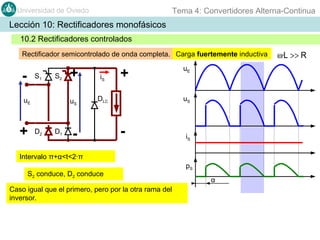
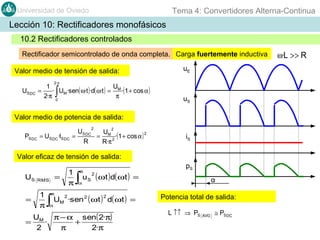
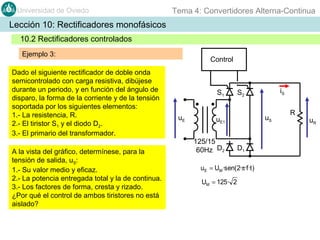
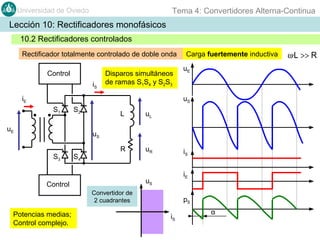
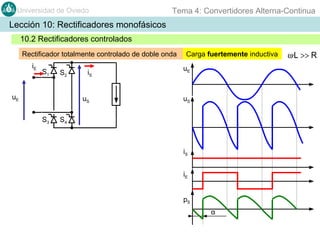
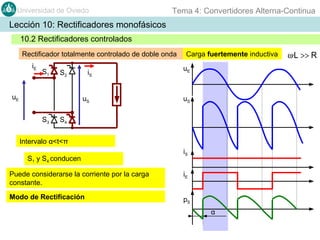
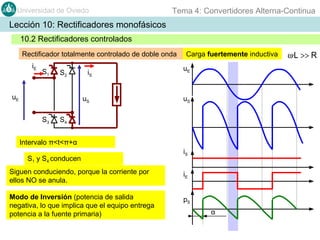
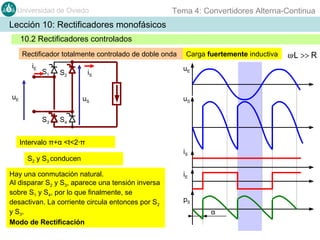
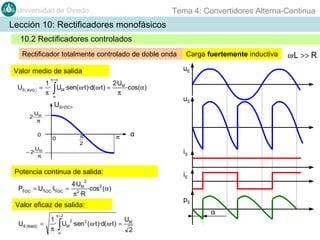
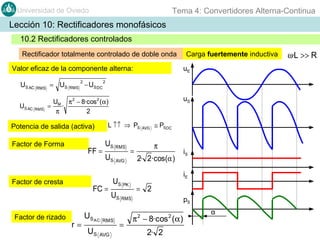
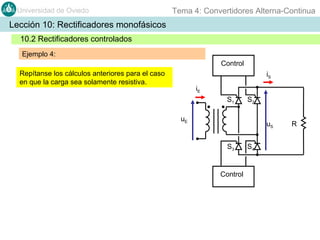
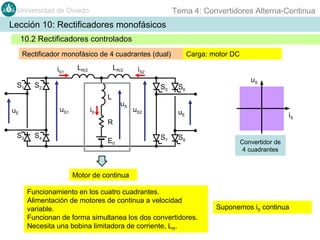
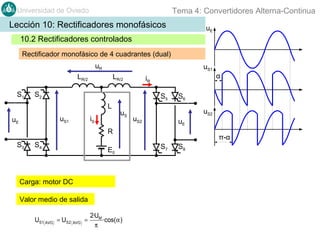
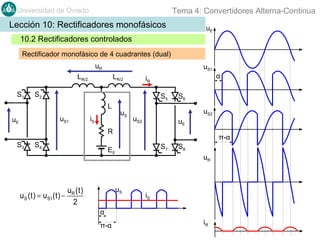
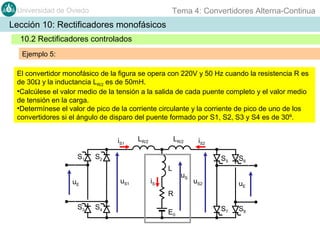
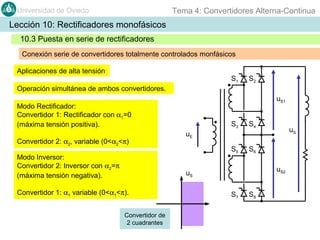
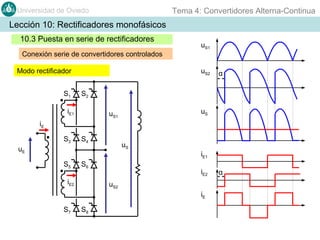
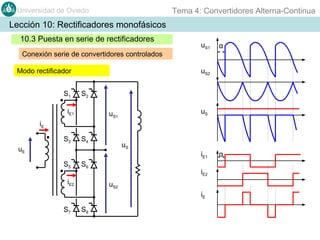
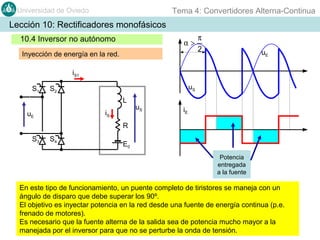
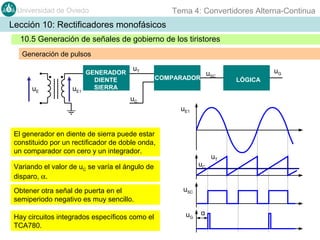
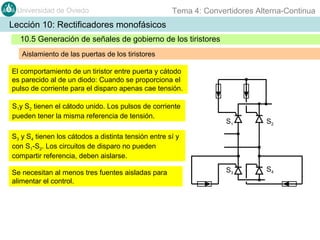
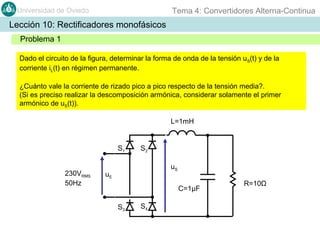
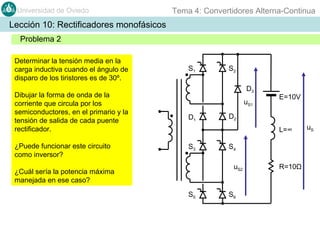
Este documento contiene información sobre convertidores de corriente alterna a continua (rectificadores). Se describen diferentes tipos de rectificadores monofásicos no controlados, como los de media onda y doble onda, y sus características con cargas resistivas e inductivas. También se explican conceptos como los valores promedio, eficaz y de rizado de la tensión de salida, así como factores de forma y cresta. Por último, se incluye un ejemplo numérico para ilustrar el funcionamiento de un rectificador de doble onda con carga induct

1. Universidad de Oviedo
Tema 4: Convertidores Alterna-Continua
TEMA 4 Convertidores alterna-continua
Lección 9: Introducción
Lección 10: Rectificadores monofásicos
Lección 11: Rectificadores trifásicos

2. Universidad de Oviedo
Tema 4: Convertidores Alterna-Continua
TEMA 4 Convertidores alterna-continua
Lección 10: Rectificadores monofásicos
10.1 Rectificadores no controlados de media y doble onda
10.2 Rectificadores controlados
10.2.1 Circuitos de media onda
10.2.2 Semiconvertidor monofásico
10.2.3 Convertidor monofásico de dos cuadrantes
10.2.4 Convertidor monofásico de cuatro cuadrantes
10.3 Puesta en serie de rectificadores monofásicos
10.3.1 Convertidor monofásico en serie
10.4 Funcionamiento en modo inversor no autónomo
10.5 Generación de señales de gobierno

3. Tema 4: Convertidores Alterna-Continua
Universidad de Oviedo
Lección 10: Rectificadores monofásicos
10.1 Rectificadores no controlados de media y doble onda
Circuito de media onda, carga resistiva
D
iS
R
uE
uE
uS
uS
iS
Potencias bajas
Tensiones de salida bajas
U ·senωt 0 ≤ t ≤ T 2
uS ( t ) =  M
T 2≤t≤T
0
uS ( t ) =
pS
UM  π
2

 1 + senω t − cos 2ω t + ....
π  2
3

uS
Valores medios de tensión, corriente y potencia:
US
AVG
=
UM
π
IS
AVG
=
UM
π·R
Convertidor de
1 cuadrante
2
Carga
resistiva
PS DC = PS AVG =
UM
π 2 ·R
iS

4. Tema 4: Convertidores Alterna-Continua
Universidad de Oviedo
Lección 10: Rectificadores monofásicos
10.1 Rectificadores no controlados de media y doble onda
Circuito de media onda, carga resistiva
uE
U ·senωt 0 ≤ t ≤ T 2
uS ( t ) =  M
T 2≤t≤T
0
uS ( t ) =
UM  π
2

 1 + senω t − cos 2ω t + ....
π  2
3

uS
Valores eficaz de salida:
iS
T
US
RMS
=
U
1
u S ( t )2 dt = M
T0
2
∫
pS
Valores eficaz de salida de la componente alterna:
US AC
2
RMS
2
= US RMS − US =
UM
· π2 − 4
2·π
Valor eficaz del primer armónico de tensión:
2 T
A 1 = · u S ( t )·cos( ω·t ) dt
T 0
∫
2 T
B1 = · u S ( t )·sen( ω·t ) dt
T 0
∫
2
US1 RMS =
2
A 1 + B1
2
=
UM
2· 2
, f1 = fred

5. Tema 4: Convertidores Alterna-Continua
Universidad de Oviedo
Lección 10: Rectificadores monofásicos
10.1 Rectificadores no controlados de media y doble onda
Circuito de media onda, carga resistiva
uE
U ·senωt 0 ≤ t ≤ T 2
uS ( t ) =  M
T 2≤t≤T
0
uS ( t ) =
UM  π
2

 1 + senω t − cos 2ω t + ....
π  2
3

uS
Potencia total de salida (aparente):
iS
2
PS
RMS
= US
RMS
·IS
RMS
U
= M
4·R
Factor de forma:
FF =
US RMS
US AVG
pS
Factor de cresta
U π
π
= M·
=
2 UM 2
FC =
US PK
US RMS
= UM ·
2
=2
UM
Factor de rizado
r=
US AC
US
RMS
AVG
U
π
= M · π 2 − 4·
=
2·π
UM
π2 − 4
= 1.21
2

6. Tema 4: Convertidores Alterna-Continua
Universidad de Oviedo
Lección 10: Rectificadores monofásicos
10.1 Rectificadores no controlados de media y doble onda
uE
Circuito de media onda, carga inductiva
L
iS
D
uL
uE
R
iS
uS
La corriente de salida, iS, no tiene la misma
forma que la tensión de salida, uS.
di ( t )
UM ·sen( ω·t ) = R·iS ( t ) + L· S
dt
Valor medio de
tensión
uS
US
AVG
=
UM
·(1 − cos β )
2·π
Menor que en el caso
de carga resistiva
uL
β
pS
uS
Convertidor de
2 cuadrantes
iS

7. Tema 4: Convertidores Alterna-Continua
Universidad de Oviedo
Lección 10: Rectificadores monofásicos
10.1 Rectificadores no controlados de media y doble onda
Ejemplo: Sea el circuito de la figura, donde se conocen L y R.Si uE(t) es senoidal pura, de
frecuencia angular ω y de valor máximo UM. ¿A qué ángulo β el diodo deja de conducir?
uE
L
iS
D
uL
uE
R
uS
uS
iS
Hay que resolver la ecuación
diferencial, para calcular la corriente
UM ·sen( ω·t ) = R·iS ( t ) + L·
U
iS ( t ) = M
Z
β·T
2·π
di S ( t )
dt

sen( ω·t − φ ) + e


T
ωt
−
tg φ

·sen( φ ) 


Z = R 2 + ( ω·L )
donde
 ω·L 
φ = arctg

R 

2

8. Tema 4: Convertidores Alterna-Continua
Universidad de Oviedo
Lección 10: Rectificadores monofásicos
10.1 Rectificadores no controlados de media y doble onda
Ejemplo: Sea el circuito de la figura, donde se conocen L y R.Si uE(t) es senoidal pura, de
frecuencia angular ω y de valor máximo UM. ¿A qué ángulo β el diodo deja de conducir?
uE
L
iS
D
uL
uE
R
uS
Cuando
β·T
t=
2·π
uS
debe cumplirse
 β·T

sen ω·
− φ = e
 2·π

β· T
− 2·π
tg φ
iS ( t ) = 0
iS
β·T
2·π
T
ω·
·sen( φ )
Esta ecuación debe ser calculada numéricamente

9. Tema 4: Convertidores Alterna-Continua
Universidad de Oviedo
Lección 10: Rectificadores monofásicos
10.1 Rectificadores no controlados de media y doble onda
uE
Circuito de doble onda, carga resistiva
D1
D2
iS
uE
R
uS
uS
iS
D3
D4
pS

10. Tema 4: Convertidores Alterna-Continua
Universidad de Oviedo
Lección 10: Rectificadores monofásicos
10.1 Rectificadores no controlados de media y doble onda
uE
Circuito de doble onda, carga resistiva
uE
+
D1
D2
iS
+
+
uS
R
-
D3
D4
-
uS
iS
pS

11. Tema 4: Convertidores Alterna-Continua
Universidad de Oviedo
Lección 10: Rectificadores monofásicos
10.1 Rectificadores no controlados de media y doble onda
uE
Circuito de doble onda, carga resistiva
uE
-
D1
D2
iS
-
+
uS
R
+
+
D3
D4
-
uS
iS
pS

12. Tema 4: Convertidores Alterna-Continua
Universidad de Oviedo
Lección 10: Rectificadores monofásicos
10.1 Rectificadores no controlados de media y doble onda
uE
Circuito de doble onda, carga resistiva
D1
D2
iS
uE
R
uS
uS
iS
D3
D4
pS
Potencias altas, Tensiones de salida altas
uS ( t ) = UM · senωt
uS ( t ) =
uS
4·UM  1 1
1

· + cos( 2·ω·t ) − cos( 4·ω·t ) + ...
π 2 3
15

Convertidor de
1 cuadrante
Valores medios de tensión, corriente y potencia:
US
AVG
2·UM
=
π
IS
AVG
2·UM
=
π·R
2
Carga
PS DC = PS AVG
4·U
= 2M
π ·R
iS

13. Tema 4: Convertidores Alterna-Continua
Universidad de Oviedo
Lección 10: Rectificadores monofásicos
10.1 Rectificadores no controlados de media y doble onda
Circuito de doble onda, carga resistiva
uE
uS ( t ) = UM · senωt
uS ( t ) =
4·UM  1 1
1

· + cos( 2·ω·t ) − cos( 4·ω·t ) + ...
π 2 3
15

uS
Valores eficaz de salida:
US
RMS
=
1
T
T
∫
u S ( t ) 2 dt =
iS
UM
2
0
Valores eficaz de salida de la componente alterna:
US AC
2
RMS
= US RMS − US
2
AVG
2
=
pS
2
UM 4·UM
UM π 2 − 8
−
=
·
4
π
π
2
Valor eficaz del primer armónico de tensión:
2 T
A 1 = · u S ( t )·cos( ω·t ) dt
T 0
∫
2 T
B1 = · u S ( t )·sen( ω·t ) dt
T 0
∫
2
US1 RMS =
2
A 1 + B1
2
=
4·UM
3·π· 2
, f1 = 2·fred

14. Tema 4: Convertidores Alterna-Continua
Universidad de Oviedo
Lección 10: Rectificadores monofásicos
10.1 Rectificadores no controlados de media y doble onda
Circuito de doble onda, carga resistiva
uE
uS ( t ) = UM · senωt
uS ( t ) =
4·UM  1 1
1

· + cos( 2·ω·t ) − cos( 4·ω·t ) + ...
π 2 3
15

uS
Potencia total de salida (aparente):
iS
2
PS
RMS
= US
RMS
·IS
RMS
U
= M
2·R
Factor de forma:
FF =
US RMS
US AVG
Factor de cresta
U π
π
= M·
=
2 UM 2· 2
FC =
Factor de rizado
r=
US AC
RMS
US AVG
= ... =
π2 − 8
2· 2
= 0.48
US PK
US RMS
= UM ·
pS
2
= 2
UM

15. Universidad de Oviedo
Tema 4: Convertidores Alterna-Continua
Lección 10: Rectificadores monofásicos
10.1 Rectificadores no controlados de media y doble onda
Circuito de doble onda, carga inductiva
Ejemplo 1:
Dado el siguiente rectificador de doble onda con
carga inductiva, dibújese durante un periodo la
forma de la corriente y de la tensión soportada
por los siguientes elementos:
1.- La resistencia, R, y la asociación serie R, L.
2.- El diodo D1.
3.- El secundario del transformador.
A la vista del gráfico, determínese, para la
tensión de salida, uS,
1.- Su valor medio y eficaz.
2.- La potencia entregada total y la de continua.
3.- Los factores de forma, cresta y rizado.
4.- Valor mínimo de L para que la corriente no
se anule en todo el periodo.
D1
D2
iS
uS
uE
D3
D4
uL
uR
L
R
L = 50mH
R = 10 Ω
uE = 2 ·230·sen(100·π·t )
rt =
N2
12
=
N1
230
230 VRMS
50 Hz

16. Tema 4: Convertidores Alterna-Continua
Universidad de Oviedo
Lección 10: Rectificadores monofásicos
10.1 Rectificadores no controlados de media y doble onda
Circuito de doble onda, carga inductiva
A la salida del rectificador la forma de onda de
tensión es conocida.
uS ( t ) =
N2
· uE ( t ) =
N1
D1
D2
iS
uS
uE
uL
2 ·12· sen(100·π·t )
D3
D4
uR
L
R
Descomponiendo en series de Fourier:
4· 2·12  1 1
1

uS ( t ) =
· + cos( 200·π·t ) − cos( 400·π·t ) + ...
π
15
2 3

17.0V
=
10.8V
Tomando el primer armónico (simplificación)
uS ( t ) =
24· 2 16· 2
+
·cos( 200·π·t )
π
π
+
7.20V

17. Tema 4: Convertidores Alterna-Continua
Universidad de Oviedo
Lección 10: Rectificadores monofásicos
10.1 Rectificadores no controlados de media y doble onda
Circuito de doble onda, carga inductiva
D1
A la salida del rectificador la forma de onda de
tensión es conocida.
uS ( t ) =
N2
· uE ( t ) =
N1
D2
iS
uS
uE
uL
2 ·12· sen(100·π·t )
D3
uR
D4
Puede resolverse por superposición (Fourier)
DC
AC (Aproximación del primer armónico)
uS
Z L = j·ωL = 0
·
uS
f = 100 Hz ⇒ ω = 200·π
Z L = j·ωL = j·200·π·50·10 −3 = 10·π· j
·
L
R

18. Tema 4: Convertidores Alterna-Continua
Universidad de Oviedo
Lección 10: Rectificadores monofásicos
10.1 Rectificadores no controlados de media y doble onda
Circuito de doble onda, carga inductiva
DC
iS DC =
US DC
R
=
24· 2
= 1.08 A
π·10
iS DC = iR DC = iL DC
uS
u S DC = uR DC ; uL DC = 0
AC (Aproximación del primer armónico)
iS AC
=
RMS
=
US AC
RMS
Z
=
 R 
R 2 + L2 ·ω2 ∠arctg

 L·ω
5,09 ∠90 º
= 0,15 ∠82,3º
33,0∠ ,7º
17
iS AC
PK
= 0,22 ∠82,3º
16
∠90 º
π
=
uS

19. Tema 4: Convertidores Alterna-Continua
Universidad de Oviedo
Lección 10: Rectificadores monofásicos
10.1 Rectificadores no controlados de media y doble onda
Circuito de doble onda, carga inductiva
iS DC =
iS AC
iS
PK
US DC
PK
R
=
17,0V
24· 2
= 108 A
,
π·10
7,20V
= 0,22 ∠82,3º
= iS DC + iS AC
PK
=
90º
= 108 A + 0,22 A = 130 A
,
,
82,3º
1,08A
1,30A

20. Tema 4: Convertidores Alterna-Continua
Universidad de Oviedo
Lección 10: Rectificadores monofásicos
10.2 Rectificadores controlados
Rectificador controlado de media onda.
Carga resistiva
iS
uE
S
uE
R
uS
uS
iS
Potencias bajas, tensiones de salida bajas
α·π

0
0≤t<

180·ω

α·π
π

uS ( t ) = UM ·sen( ω·t )
≤t <
180·ω
ω

π
2·π

0
≤t<

ω
ω

pS
α
Valores medios de tensión, corriente y potencia:
US DC
U
= M ·(1 + cos α )
2·π
PS DC =
US DC
R
2
2
UM
2
=
·(1 + cos α )
4·π 2 ·R
uS
Convertidor de
1 cuadrante
iS

21. Tema 4: Convertidores Alterna-Continua
Universidad de Oviedo
Lección 10: Rectificadores monofásicos
10.2 Rectificadores controlados
Rectificador controlado de media onda.
US DC
U
= M ·(1 + cos α )
2·π
UM
π
UM
2·π
0
Valor eficaz de salida:
US
1
T
=
RMS
T
∫
u S ( t ) dt =
2
0
π
=
1
2
2
UM ·sen( ϑ) dϑ =
2·π α
∫
ω
2·π
2· π
∫
USDC
uS
π
2
0
π
α
iS
2
pS
1
2  1 − cos ( 2·ϑ) 
UM ·
dϑ =
2·π α
2


π
∫
=
=
UM  π − α sen( 2·α)  UM
+

=
2·π  2
4
2

2
uE
 ϑ ϑ
uS   d
=
ω ω

0
π
π
2

UM  1
cos( 2·ϑ)

dϑ −
dϑ =

2·π  α 2
2
α


∫
Carga resistiva
∫
2
UM
2·π
 ϑ π sen( 2·ϑ)

−
2 α
4

π − α sen( 2·α)
+
π
2·π
α

=

α
π

22. Tema 4: Convertidores Alterna-Continua
Universidad de Oviedo
Lección 10: Rectificadores monofásicos
10.2 Rectificadores controlados
Rectificador controlado de media onda.
US DC =
Carga resistiva
uE
UM
·(1 + cos α )
2·π
uS
iS
Potencia total de salida (aparente):
U
sen( 2·α) 

= M · π − α +

4·π·R 
2

2
PS
RMS
= US
Factor de forma:
FF =
US RMS
US AVG
Factor de rizado
r=
US AC
US
RMS
AVG
RMS
·IS
RMS
pS
Factor de cresta
FC =
US PK
US RMS
α

23. Tema 4: Convertidores Alterna-Continua
Universidad de Oviedo
Lección 10: Rectificadores monofásicos
10.2 Rectificadores controlados
Rectificador controlado de media onda.
Carga resistiva
iS
uE
S
uE
R
uS
uS
iS
Potencias bajas, tensiones de salida bajas
α·π

0
0≤t<

180·ω

α·π
π

uS ( t ) = UM ·sen( ω·t )
≤t <
180·ω
ω

π
2·π

0
≤t<

ω
ω

pS
α
Valores medios de tensión, corriente y potencia:
US DC
U
= M ·(1 + cos α )
2·π
PS DC =
US DC
R
2
2
UM
2
=
·(1 + cos α )
4·π 2 ·R
uS
Convertidor de
1 cuadrante
iS

24. Tema 4: Convertidores Alterna-Continua
Universidad de Oviedo
Lección 10: Rectificadores monofásicos
10.2 Rectificadores controlados
Rectificador controlado de media onda.
iS
S
uE
Carga inductiva
uE
L
uL
uS
R
uR
uS
iS
Potencias bajas, tensiones de salida bajas
α·π

0
0≤t<

180·ω

α·π
β·π

uS ( t ) = UM ·sen( ω·t )
≤t
<
180·ω
180·ω

β·π
2·π

0
≤t<

180·ω
ω

uL
pS
α
π
β
2·π

25. Tema 4: Convertidores Alterna-Continua
Universidad de Oviedo
Lección 10: Rectificadores monofásicos
10.2 Rectificadores controlados
Rectificador controlado de media onda.
Carga inductiva
uE
Valor medios de tensión.
US DC =
UM
·( cos α − cos β )
2·π
uS
Entre α y π funciona en modo rectificador,
inyectándose potencia en la carga.
Entre π y β funciona en modo inversor,
devolviendo potencia a la entrada.
iS
uL
pS
uS
Convertidor de
2 cuadrantes
α
iS
π
β
2·π

26. Tema 4: Convertidores Alterna-Continua
Universidad de Oviedo
Lección 10: Rectificadores monofásicos
10.2 Rectificadores controlados
Rectificador semicontrolado de onda completa. Carga resistiva
S1
iS
S2
uE
uS
D2
D1
uE
R
uR
uS
iS
pS
α

27. Tema 4: Convertidores Alterna-Continua
Universidad de Oviedo
Lección 10: Rectificadores monofásicos
10.2 Rectificadores controlados
Rectificador semicontrolado de onda completa. Carga resistiva
S1
iS
S2
uE
uS
D2
uE
R
D1
Entre 0 y α, no circula corriente.
uR
uS
iS
pS
α

28. Tema 4: Convertidores Alterna-Continua
Universidad de Oviedo
Lección 10: Rectificadores monofásicos
10.2 Rectificadores controlados
Rectificador semicontrolado de onda completa. Carga resistiva
S1
iS
S2
uE
uS
D2
uE
R
uR
uS
iS
D1
pS
Entre 0 y α, no circula corriente.
Entre α y π, circula corriente proporcional a uE
α
Valor medio de tensión.
US DC
U
= M ·(1 + cos α )
π
PS DC =
US DC
R
2
2
U
2
= 2M ·(1 + cos α )
π ·R
Convertidor de
1 cuadrante
iS

29. Tema 4: Convertidores Alterna-Continua
Universidad de Oviedo
Lección 10: Rectificadores monofásicos
10.2 Rectificadores controlados
Rectificador semicontrolado de onda completa. Carga fuertemente inductiva
S1
uE
iS
S2
L
uE
uS
DLC
R
D2
D1
S1
S2
uL
uS
uR
iS
iS
pS
α
uE
uS
D2
D1
DLC
ω·L >> R

30. Tema 4: Convertidores Alterna-Continua
Universidad de Oviedo
Lección 10: Rectificadores monofásicos
10.2 Rectificadores controlados
Rectificador semicontrolado de onda completa. Carga fuertemente inductiva
S1
iS
S2
uE
uS
D2
D1
DLC
uE
uS
iS
pS
α
ω·L >> R

31. Tema 4: Convertidores Alterna-Continua
Universidad de Oviedo
Lección 10: Rectificadores monofásicos
10.2 Rectificadores controlados
Rectificador semicontrolado de onda completa. Carga fuertemente inductiva
+
S1
S2
uE
-
+
uS
D2
D1
iS
+
DLC
-
uE
uS
-
iS
Intervalo α<t<π
S1 conduce, D1 conduce
Puede considerarse la corriente por la carga constante.
pS
α
ω·L >> R

32. Tema 4: Convertidores Alterna-Continua
Universidad de Oviedo
Lección 10: Rectificadores monofásicos
10.2 Rectificadores controlados
Rectificador semicontrolado de onda completa. Carga fuertemente inductiva
S1
iS
S2
uE
uS
D2
DLC
D1
ω·L >> R
uE
uS
iS
Intervalo π<t<π+α
S1 apagado, D1 no conduce
pS
α
DLC es el diodo de libre circulación; se coloca para que
la corriente por la carga pueda circular cuando la
tensión de entrada es nula.
En ese instante, DLC conduce, y la corriente por S1 se anula (el tiristor se apaga, y S1 y D1
quedan polarizados inversamente).

33. Tema 4: Convertidores Alterna-Continua
Universidad de Oviedo
Lección 10: Rectificadores monofásicos
10.2 Rectificadores controlados
Rectificador semicontrolado de onda completa. Carga fuertemente inductiva
-
S2
uE
+
D2
D1
+
iS
uS
S1
DLC
-
+
uE
uS
-
iS
Intervalo π+α<t<2·π
S2 conduce, D2 conduce
Caso igual que el primero, pero por la otra rama del
inversor.
pS
α
ω·L >> R

34. Tema 4: Convertidores Alterna-Continua
Universidad de Oviedo
Lección 10: Rectificadores monofásicos
10.2 Rectificadores controlados
Rectificador semicontrolado de onda completa. Carga fuertemente inductiva
S1
iS
S2
uE
uS
D2
uE
DLC
uS
D1
iS
Intervalo 2·π<t<2·π+α
pS
S2 apagado, D2 no conduce
Caso idéntico al segundo
subintervalo. El diodo de
libre circulación conduce la
corriente por la carga.
α
Convertidor de
1 cuadrante
iS
ω·L >> R

35. Tema 4: Convertidores Alterna-Continua
Universidad de Oviedo
Lección 10: Rectificadores monofásicos
10.2 Rectificadores controlados
Rectificador semicontrolado de onda completa. Carga fuertemente inductiva
Valor medio de tensión de salida:
uE
2· π
US DC
U
1
=
· UM ·sen( ω·t )·d( ω·t ) = M ·(1 + cos α )
2·π 0
π
∫
uS
Valor medio de potencia de salida:
PS DC = US DC ·IS DC =
US DC
2
R
2
U
2
= M 2 ·(1 + cos α )
R·π
iS
Valor eficaz de tensión de salida:
US
=
RMS
1
π
1
π
=
π
∫
α
π
∫
α
u S ( ω t )d( ω t ) =
·
·
2
UM ·sen 2 ( ω t ) d( ω t ) =
·
·
2
pS
2
U
π − α sen( 2·π)
= M·
+
2
π
2·π
α
Potencia total de salida:
L ↑↑ ⇒ PS
AVG
≅ PS DC
ω·L >> R

36. Universidad de Oviedo
Tema 4: Convertidores Alterna-Continua
Lección 10: Rectificadores monofásicos
10.2 Rectificadores controlados
Ejemplo 3:
Dado el siguiente rectificador de doble onda
semicontrolado con carga resistiva, dibújese
durante un periodo, y en función del ángulo de
disparo, la forma de la corriente y de la tensión
soportada por los siguientes elementos:
1.- La resistencia, R.
2.- El tiristor S1 y el diodo D2.
3.- El primario del transformador.
A la vista del gráfico, determínese, para la
tensión de salida, uS:
1.- Su valor medio y eficaz.
2.- La potencia entregada total y la de continua.
3.- Los factores de forma, cresta y rizado.
¿Por qué el control de ambos tiristores no está
aislado?
Control
S1
uE
uS
uE1
125/15
60Hz D2
D1
uE = UM ·sen(2·π·f ·t )
UM = 125· 2
iS
S2
R
uR

37. Tema 4: Convertidores Alterna-Continua
Universidad de Oviedo
Lección 10: Rectificadores monofásicos
10.2 Rectificadores controlados
Rectificador totalmente controlado de doble onda
Control
iS
Disparos simultáneos
de ramas S1S4 y S2S3
iE
Carga fuertemente inductiva
uE
uS
S1
S2
uE
L
uL
R
uR
uS
S3
S4
iS
iE
uS
Control
Convertidor de
2 cuadrantes
Potencias medias;
Control complejo.
pS
iS
α
ω·L >> R

38. Universidad de Oviedo
Tema 4: Convertidores Alterna-Continua
Lección 10: Rectificadores monofásicos
10.2 Rectificadores controlados
Rectificador totalmente controlado de doble onda
iE
S1
S2
uE
iS
uS
S3
Carga fuertemente inductiva
uE
uS
S4
iS
iE
pS
α
ω·L >> R

39. Universidad de Oviedo
Tema 4: Convertidores Alterna-Continua
Lección 10: Rectificadores monofásicos
10.2 Rectificadores controlados
Rectificador totalmente controlado de doble onda
iE
S1
iS
S2
uE
uS
S3
Carga fuertemente inductiva
uE
uS
S4
Intervalo α<t<π
S1 y S4 conducen
iS
Puede considerarse la corriente por la carga
constante.
iE
Modo de Rectificación
pS
α
ω·L >> R

40. Universidad de Oviedo
Tema 4: Convertidores Alterna-Continua
Lección 10: Rectificadores monofásicos
10.2 Rectificadores controlados
Rectificador totalmente controlado de doble onda
iE
S1
S2
uE
iS
uS
S3
Carga fuertemente inductiva
uE
uS
S4
Intervalo π<t<π+α
S1 y S4 conducen
iS
Siguen conduciendo, porque la corriente por
ellos NO se anula.
iE
Modo de Inversión (potencia de salida
negativa, lo que implica que el equipo entrega
potencia a la fuente primaria)
pS
α
ω·L >> R

41. Universidad de Oviedo
Tema 4: Convertidores Alterna-Continua
Lección 10: Rectificadores monofásicos
10.2 Rectificadores controlados
Rectificador totalmente controlado de doble onda
iE
S1
iS
S2
uE
uS
S3
Carga fuertemente inductiva
uE
uS
S4
Intervalo π+α <t<2·π
S2 y S3 conducen
Hay una conmutación natural.
Al disparar S2 y S3, aparece una tensión inversa
sobre S1 y S4, por lo que finalmente, se
desactivan. La corriente circula entonces por S2
y S 3.
Modo de Rectificación
iS
iE
pS
α
ω·L >> R

42. Tema 4: Convertidores Alterna-Continua
Universidad de Oviedo
Lección 10: Rectificadores monofásicos
10.2 Rectificadores controlados
Rectificador totalmente controlado de doble onda
Carga fuertemente inductiva
uE
Valor medio de salida
π+ α
US
AVG
2·UM
1
= · UM ·sen(ω·t )·d(ω·t ) =
·cos(α )
π α
π
∫
US<DC>
2·
uS
UM
π
0
− 2·
π
2
0
UM
π
π
α
iS
Potencia continua de salida:
2
PS DC = US DC ·IS DC =
4·UM
·cos 2 ( α )
2
π ·R
Valor eficaz de salida:
π+2
US RMS =
U
1
2
· UM ·sen 2 ( ω·t )·d( ω·t ) = M
π α
2
∫
iE
pS
α
ω·L >> R

43. Tema 4: Convertidores Alterna-Continua
Universidad de Oviedo
Lección 10: Rectificadores monofásicos
10.2 Rectificadores controlados
Rectificador totalmente controlado de doble onda
Valor eficaz de la componente alterna:
2
US AC RMS = US RMS − US DC
US AC RMS
uE
2
uS
UM π 2 − 8·cos 2 (α )
=
·
π
2
L ↑↑ ⇒ PS
Potencia de salida (activa)
Factor de Forma
FF =
Factor de cresta
Factor de rizado
US RMS
US AVG
FC =
r=
US AC
US
Carga fuertemente inductiva
US PK
US RMS
RMS
AVG
=
AVG
≅ PS DC
π
2· 2·cos(α )
iE
= 2
pS
π − 8·cos (α )
2
=
iS
2
2· 2
α
ω·L >> R

44. Universidad de Oviedo
Tema 4: Convertidores Alterna-Continua
Lección 10: Rectificadores monofásicos
10.2 Rectificadores controlados
Ejemplo 4:
Control
Repítanse los cálculos anteriores para el caso
en que la carga sea solamente resistiva.
iS
iE
S1
S2
uE
uS
S3
Control
S4
R

45. Tema 4: Convertidores Alterna-Continua
Universidad de Oviedo
Lección 10: Rectificadores monofásicos
10.2 Rectificadores controlados
Rectificador monofásico de 4 cuadrantes (dual)
iS1
S1
LR/2
LR/2
iS2
S2
S5
L
uS1
uE
iS
uS
Carga: motor DC
uS2
S6
uS
uE
iS
R
S3
S4
E0
S7
S8
Convertidor de
4 cuadrantes
Motor de continua
Funcionamiento en los cuatro cuadrantes.
Alimentación de motores de continua a velocidad
variable.
Funcionan de forma simultanea los dos convertidores.
Necesita una bobina limitadora de corriente, LR.
Suponemos iS continua

46. Tema 4: Convertidores Alterna-Continua
Universidad de Oviedo
Lección 10: Rectificadores monofásicos
uE
10.2 Rectificadores controlados
Rectificador monofásico de 4 cuadrantes (dual)
uR
uS1
LR/2
S1
LR/2
S2
S5
L
uS1
uE
α
iR
iS
uS
S6
uS2
uS2
uE
R
S3
S4
E0
Carga: motor DC
Valor medio de salida
US1 AVG = US 2 AVG =
2·UM
·cos( α )
π
π-α
S7
S8

47. Tema 4: Convertidores Alterna-Continua
Universidad de Oviedo
Lección 10: Rectificadores monofásicos
uE
10.2 Rectificadores controlados
Rectificador monofásico de 4 cuadrantes (dual)
uR
uS1
LR/2
S1
LR/2
S2
S5
L
uS1
uE
α
iR
iS
uS
S6
uS2
uS2
uE
R
S3
S4
π-α
S7
E0
uR
uS
u (t)
uS ( t ) = uS1( t ) − R
2
S8
iS
α
π-α
iR

48. Universidad de Oviedo
Tema 4: Convertidores Alterna-Continua
Lección 10: Rectificadores monofásicos
10.2 Rectificadores controlados
Rectificador monofásico de 4 cuadrantes (dual)
•Para trabajar en los cuatro cuadrantes se conectan dos convertidores monofásicos
completos “espalda contra espalda”.
•Los ángulos de retraso se controlan de tal forma que uno funciona como rectificador y el
otro como inversor.
•El valor medio de las tensiones de salida de ambos convertidores debe ser el mismo.
•Como la corriente de salida de ambos convertidores no está en fase habrá corriente
circulante entre ellos, limitada por una inductancia LR.
•Sin corriente circulante funciona solamente un convertidor, estando el otro bloqueado
gracias al manejo de las puertas.
•El funcionamiento con corriente circulante presenta una serie de ventajas:
•El flujo de potencia es posible en cualquier dirección y cualquier momento de forma
independiente de la carga.
•La dinámica de cambio de un cuadrante a otro es más rápida.

49. Tema 4: Convertidores Alterna-Continua
Universidad de Oviedo
Lección 10: Rectificadores monofásicos
10.2 Rectificadores controlados
Ejemplo 5:
El convertidor monofásico de la figura se opera con 220V y 50 Hz cuando la resistencia R es
de 30Ω y la inductancia LR/2 es de 50mH.
•Calcúlese el valor medio de la tensión a la salida de cada puente completo y el valor medio
de tensión en la carga.
•Determínese el valor de pico de la corriente circulante y la corriente de pico de uno de los
convertidores si el ángulo de disparo del puente formado por S1, S2, S3 y S4 es de 30º.
iS1
S1
LR/2
LR/2
iS2
S2
S5
L
uS1
uE
iS
uS
uS2
S6
uE
R
S3
S4
E0
S7
S8

50. Tema 4: Convertidores Alterna-Continua
Universidad de Oviedo
Lección 10: Rectificadores monofásicos
10.3 Puesta en serie de rectificadores
Conexión serie de convertidores totalmente controlados monfásicos
Aplicaciones de alta tensión
S1
S2
Operación simultánea de ambos convertidores.
uS1
Modo Rectificador:
Convertidor 1: Rectificador con α1=0
(máxima tensión positiva).
Convertidor 2: α2, variable (0<α2<π)
Modo Inversor:
Convertidor 2: Inversor con α2=π
(máxima tensión negativa).
S3
S4
S5
S6
uS2
uS
Convertidor 1: α1 variable (0<α1<π).
Convertidor de
2 cuadrantes
uS
uE
S7
S8

51. Tema 4: Convertidores Alterna-Continua
Universidad de Oviedo
Lección 10: Rectificadores monofásicos
10.3 Puesta en serie de rectificadores
Conexión serie de convertidores controlados
Modo rectificador
S1
uS1
uS2
α
S2
iE1
uS
uS1
iE
S3
S4
uS
uE
iE1
S5
S6
iE2
iE2
uS2
iE
S7
S8
α

52. Tema 4: Convertidores Alterna-Continua
Universidad de Oviedo
Lección 10: Rectificadores monofásicos
10.3 Puesta en serie de rectificadores
Conexión serie de convertidores controlados
Modo rectificador
S1
uS1
α
uS2
S2
iE1
uS
uS1
iE
S3
S4
uS
uE
iE1
S5
S6
iE2
iE2
uS2
iE
S7
S8
α

53. Tema 4: Convertidores Alterna-Continua
Universidad de Oviedo
Lección 10: Rectificadores monofásicos
10.4 Inversor no autónomo
α>
Inyección de energía en la red.
π
2
uE
iS1
S1
uS
S2
L
iS
uE
uS
iE
R
S3
S4
E0
Potencia
entregada
a la fuente
En este tipo de funcionamiento, un puente completo de tiristores se maneja con un
ángulo de disparo que debe superar los 90º.
El objetivo es inyectar potencia en la red desde una fuente de energía continua (p.e.
frenado de motores).
Es necesario que la fuente alterna de la salida sea de potencia mucho mayor a la
manejada por el inversor para que no se perturbe la onda de tensión.

54. Tema 4: Convertidores Alterna-Continua
Universidad de Oviedo
Lección 10: Rectificadores monofásicos
10.5 Generación de señales de gobierno de los tiristores
Generación de pulsos
uE
uE1
GENERADOR
DIENTE
SIERRA
uT
uSC
COMPARADOR
uC
uE1
El generador en diente de sierra puede estar
constituido por un rectificador de doble onda,
un comparador con cero y un integrador.
uC
Variando el valor de uC se varía el ángulo de
disparo, α.
Obtener otra señal de puerta en el
semiperiodo negativo es muy sencillo.
Hay circuitos integrados específicos como el
TCA780.
uSC
uG
α
uT
uG
LÓGICA

55. Universidad de Oviedo
Tema 4: Convertidores Alterna-Continua
Lección 10: Rectificadores monofásicos
10.5 Generación de señales de gobierno de los tiristores
Aislamiento de las puertas de los tiristores
El comportamiento de un tiristor entre puerta y cátodo
es parecido al de un diodo: Cuando se proporciona el
pulso de corriente para el disparo apenas cae tensión.
S1y S2 tienen el cátodo unido. Los pulsos de corriente
pueden tener la misma referencia de tensión.
S1
S2
S3
S4
S3 y S4 tienen los cátodos a distinta tensión entre sí y
con S1-S2. Los circuitos de disparo no pueden
compartir referencia, deben aislarse.
Se necesitan al menos tres fuentes aisladas para
alimentar el control.

56. Tema 4: Convertidores Alterna-Continua
Universidad de Oviedo
Lección 10: Rectificadores monofásicos
Problema 1
Dado el circuito de la figura, determinar la forma de onda de la tensión uS(t) y de la
corriente iL(t) en régimen permanente.
¿Cuánto vale la corriente de rizado pico a pico respecto de la tensión media?.
(Si es preciso realizar la descomposición armónica, considerar solamente el primer
armónico de uS(t)).
L=1mH
S1
230VRMS
50Hz
S2
uS
uE
C=1µF
S3
S4
R=10Ω

57. Universidad de Oviedo
Tema 4: Convertidores Alterna-Continua
Lección 10: Rectificadores monofásicos
Problema 2
Determinar la tensión media en la
carga inductiva cuando el ángulo de
disparo de los tiristores es de 30º.
Dibujar la forma de onda de la
corriente que circula por los
semiconductores, en el primario y la
tensión de salida de cada puente
rectificador.
¿Puede funcionar este circuito
como inversor?
S1
S2
D3
uS1
D1
E=10V
D2
L=∞
S3
S4
uS2
¿Cuál sería la potencia máxima
manejada en ese caso?
S5
S6
R=10Ω
uS