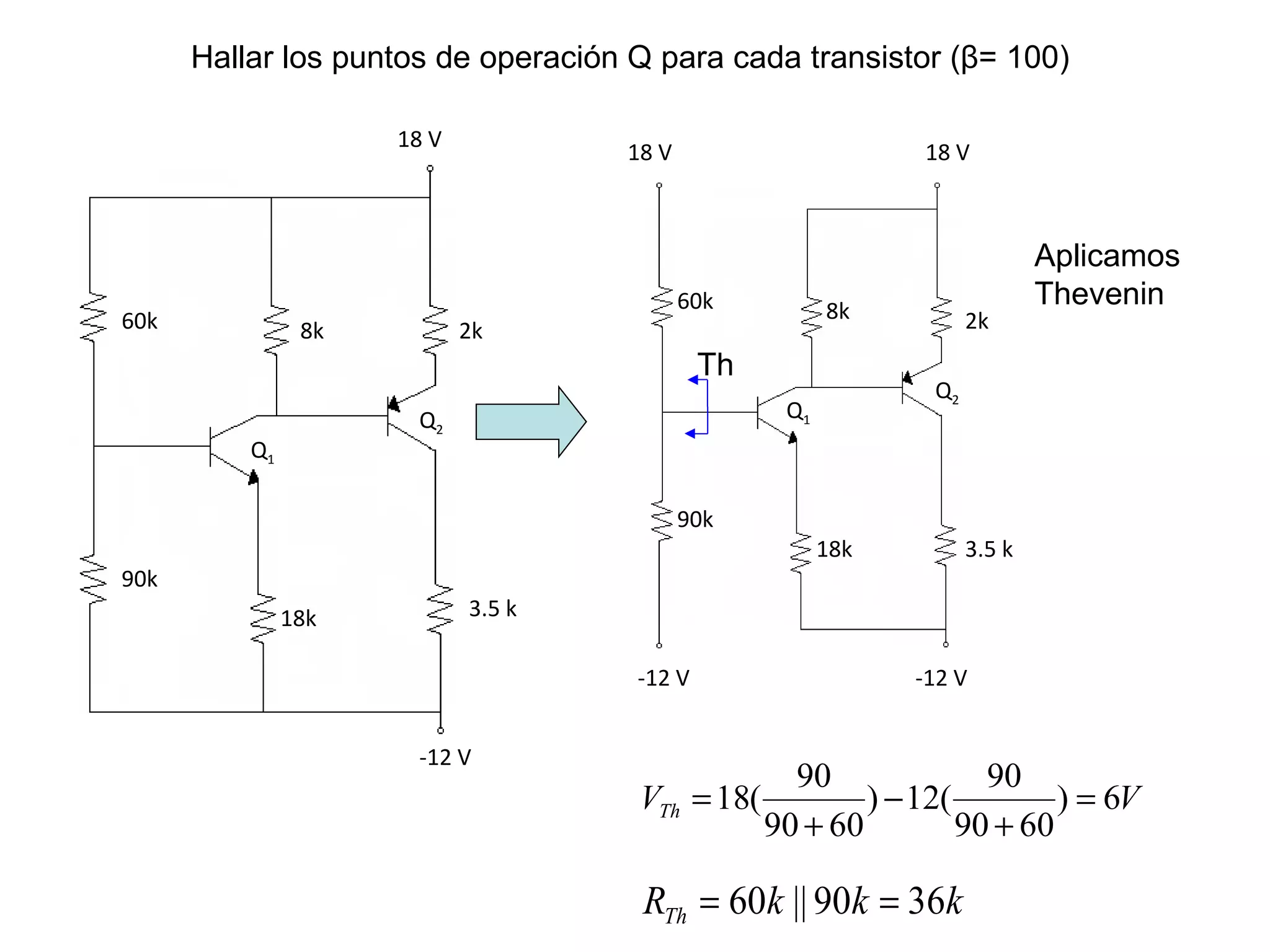
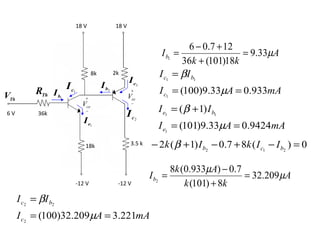
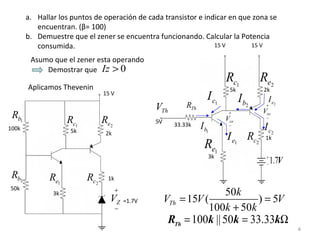
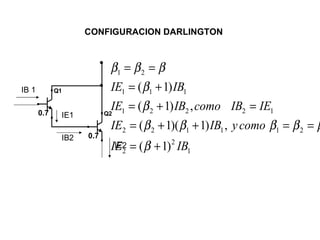
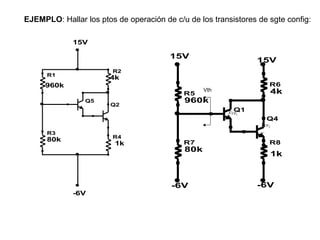
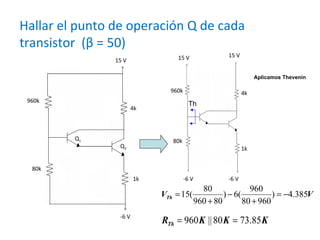
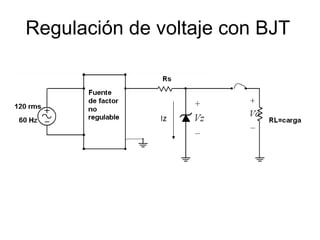
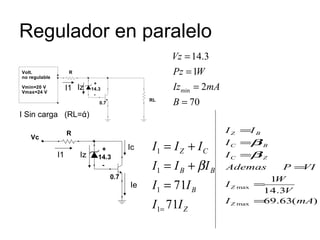
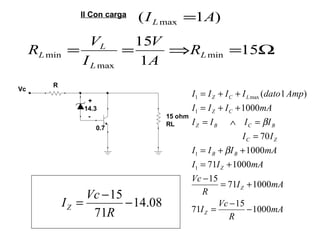
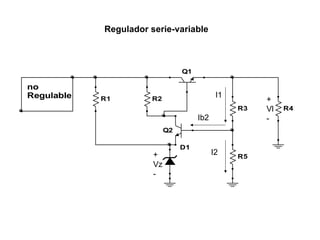
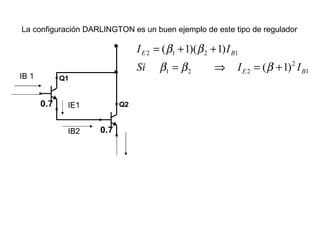
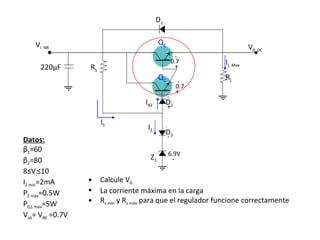
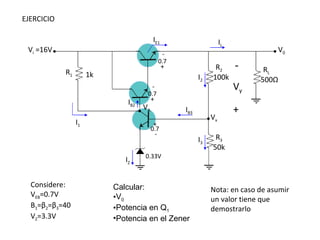
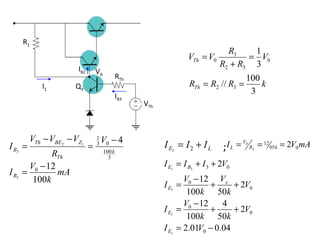
El documento presenta varios circuitos electrónicos con transistores y diodos zener. Incluye problemas para hallar puntos de operación de transistores, demostrar que un diodo zener está funcionando correctamente y calcular potencia consumida. También contiene ejemplos de reguladores de voltaje con configuraciones serie, paralelo y Darlington.

1. 18 V 2k 3.5 k 18k 8k 60k 90k Q 2 Q 1 -12 V 18 V 18 V -12 V -12 V 3.5 k 18k 90k 8k 2k 60k Aplicamos Thevenin Th Q 2 Q 1 Hallar los puntos de operación Q para cada transistor ( β = 100)

2. 2k 8k 18k 3.5 k 18 V 18 V -12 V -12 V 36k 6 V

3. >0 Q1 “Zona Activa” >0 Q2 “Zona Activa” Q 1 = Q 2 =

6. “ Zona Activa” “ Zona Activa” Zener On Como Queda demostrado que el Zener está operando

7. CONFIGURACION DARLINGTON IE2 IB 1 IE1 IB2

8. EJEMPLO : Hallar los ptos de operación de c/u de los transistores de sgte config: Vth

9. IE1 IB2 IB1 IE2

10. Hallar el punto de operación Q de cada transistor ( β = 50 ) 960k 80k 4k 1k 15 V -6 V Q 1 Q 2 Aplicamos Thevenin 15 V 15 V 4k 960k 80k 1k -6 V -6 V Th

11. 4k 1k 78.85k R Th V Th -4.385V 15 V -6 V

12. > 0 Q 1 “Zona Lineal” Q 1 = Q 2 = > 0 Q 2 “Zona Lineal”

13. Regulación de voltaje con BJT

14. Regulador serie: Diseñe una fuente de voltaje que trabaje A 15V ⇒ 1 A (maximo) + Vz -

15. Regulador serie: Sin carga (RL= ά ) Abierto, no hay corriente

16. Con Carga Máxima: Asumimos: + Vz - Ic Ie Ib

17. 2 a Zener prende 2 b Zener no se quema

19. Regulador en paralelo I Sin carga (RL= ά ) I1 Iz I1 Iz Ic Ie

20. 1 a Zener no se quema: 1 b Zener se prenda

21. II Con carga

22. 2 a Zener enciende, con Vc= Vmin 2b Para que el Zener no se queme (<Izmax)

23. Regulador serie-variable + Vz - Ib2 I1 I2 + Vl -

25. La configuración DARLINGTON es un buen ejemplo de este tipo de regulador IB 1 IE1 IB2

28. Donde: c) D 2 “ON” 0.7 6.9

32. ; LCK en el nodo A: Por lo tanto no es válida la asunción de que I B3 << I 3. Entonces aplicamos Thevenin en la base3 Como I B3 >0 Z 1 “ON”

33. ; I B2 R 1 I B3 V A I 1 R Th V Th Q 3

34. LCK en el nodo A: LVK : a) 1 2

35. b) c)