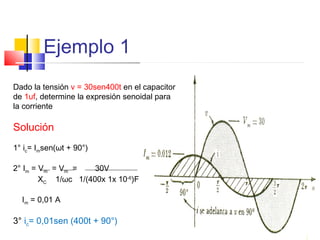
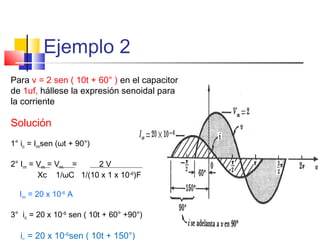
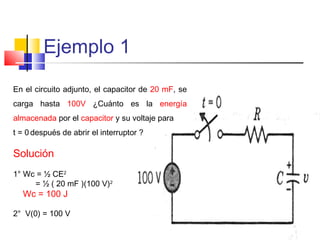
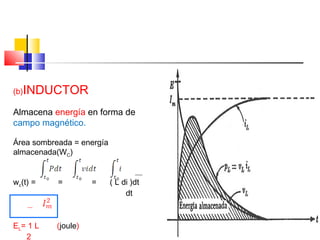
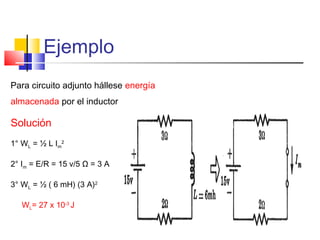
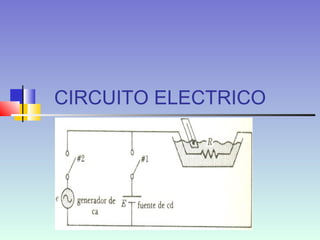
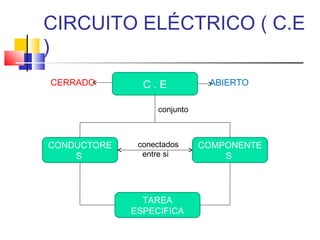
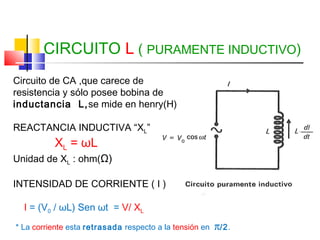
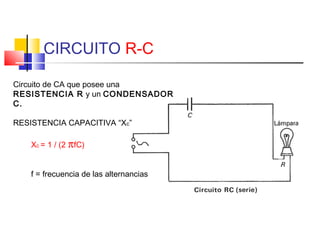
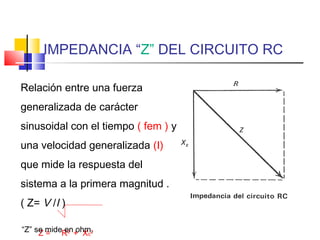
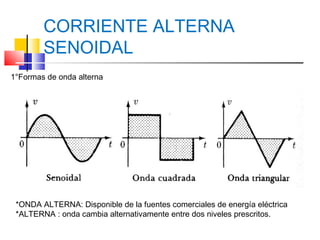
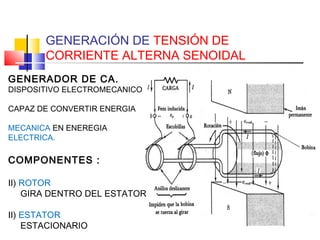
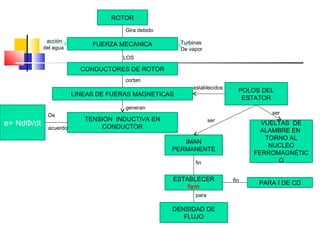
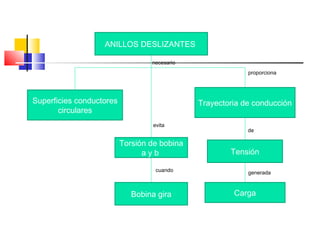
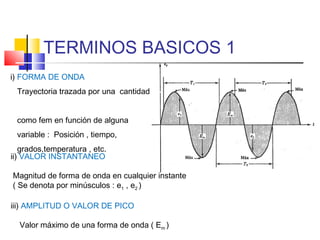
Este documento describe los diferentes tipos de circuitos eléctricos, incluyendo circuitos puramente inductivos, puramente capacitivos, R-C, R-L, y R-L-C. Explica conceptos como reactancia inductiva, reactancia capacitiva, impedancia, y desfase entre corriente e intensidad para cada circuito. También describe la generación de tensión y corriente alterna senoidal por un generador, incluyendo términos como amplitud, período, frecuencia, valor promedio y valor efectivo.

1. CIRCUITO ELECTRICO

2. CIRCUITO ELÉCTRICO ( C.E
)
CERRADO
C.E
ABIERTO
conjunto
CONDUCTORE
S
conectados
entre si
TAREA
ESPECIFICA
COMPONENTE
S

3. CIRCUITO L ( PURAMENTE INDUCTIVO)
Circuito de CA ,que carece de
resistencia y sólo posee bobina de
inductancia L, se mide en henry(H)
REACTANCIA INDUCTIVA “XL”
XL = ωL
Unidad de XL : ohm(Ω)
INTENSIDAD DE CORRIENTE ( I )
I = (V0 / ωL) Sen ωt = V/ XL
* La corriente esta retrasada respecto a la tensión en
π/2.

4. CIRCUITO C ( PURAMENTE
CAPACITIVO )
Circuito de CA que carece de
resistencia óhmica e inductiva
Sólo presenta uno ó más
condensadores de capacidad
“C”, se mide en faraday (F)
REACTANCIA CAPACITIVA “Xc”
X c = 1/ωc
Unidad de Xc : ohm (Ω)
INTENSIDAD DE CORRIENTE
I = V0 /( 1 / ωc) Sen ωT = V / Xc
* La corriente esta adelantada respecto a la tensión en
π/2

5. CIRCUITO R-C
Circuito de CA que posee una
RESISTENCIA R y un CONDENSADOR
C.
RESISTENCIA CAPACITIVA “Xc”
Xc = 1 / (2 πfC)
f = frecuencia de las alternancias

6. IMPEDANCIA “Z” DEL CIRCUITO RC
Relación entre una fuerza
generalizada de carácter
sinusoidal con el tiempo ( fem ) y
una velocidad generalizada (I)
que mide la respuesta del
sistema a la primera magnitud .
( Z= V /I )
“Z” se mideR2 + Xc2
en ohm.
Z=

7. CIRCUITO R-L
Circuito de CA que posee una resistencia
R y un inductor L.
i) REACTANCIA INDUCTIVA “ XL”
XL = ωL = 2
πfL
f = frecuencia de CA
ii) CORRIENTE EFICAZ EN CIRCUITO
( Ief )
Ief = Vef / Z ; Vef = fem eficaz
Z = impedancia
iii) IMPEDANCIA DEL CIRCUITO RL

8. CIRCUITO R-L-C ( serie )
Circuito de CA que posee una
resistencia R , una autoinducción L
y un condensador de capacidad C.
INTENSIDAD MAXIMA (I0 = Im)
I0 =
V0
(R2 + (ώL - 1 / ωc)2 )1/2
V0 = Vm = Tensión máxima

9. IMPEDANCIA ( Z ) DEL CIRCUITO R-LC
Z =
R 2 + ( X L – X C )2
DESFASE ENTRE INTENSIDAD
INSTANTANEA Y LA f.e.m DEL GENERADOR
.
Tg φ = ( XL - XC ) / R = (ωL – 1/ωC ) / R.
PERIODO DEL CIRCUITO ELÉCTRICO ( T )
T = 2π LC

10. CIRCUITO R-L-C ( PARALELO )
i) ddp instantánea V en ambas ramas es
igual.
ii) Corriente instantánea I
I = I 1 + I2
están desfasados : I1 adelante a I2
iii) I1 adelanta a V en φ1 , siendo ;
φ1 = arc tg Xc
R1
iv) I2 adelante a V en φ2 , siendo
φ2 = arc tg Xc
R2
v) I adelanta a V en φ

11. CORRIENTE ALTERNA
SENOIDAL
1°Formas de onda alterna
*ONDA ALTERNA: Disponible de la fuentes comerciales de energía eléctrica
*ALTERNA : onda cambia alternativamente entre dos niveles prescritos.

12. GENERACIÓN DE TENSIÓN DE
CORRIENTE ALTERNA SENOIDAL
GENERADOR DE CA.
DISPOSITIVO ELECTROMECANICO
CAPAZ DE CONVERTIR ENERGIA
MECANICA EN ENEREGIA
ELECTRICA.
COMPONENTES :
II) ROTOR
GIRA DENTRO DEL ESTATOR
II) ESTATOR
ESTACIONARIO

13. ROTOR
Gira debido
acción
del agua
Turbinas
De vapor
FUERZA MECANICA
LOS
CONDUCTORES DE ROTOR
cortan
LINEAS DE FUERAS MAGNETICAS
establecidos
POLOS DEL
ESTATOR
generan
e= NdΦ/dt
De
acuerdo
ser
TENSIÓN INDUCTIVA EN
CONDUCTOR
ser
VUELTAS DE
ALAMBRE EN
TORNO AL
NUCLEO
FERROMAGNÉTIC
O
IMAN
PERMANENTE
fin
ESTABLECER
fem
para
DENSIDAD DE
FLUJO
fin
PARA I DE CD

14. ANILLOS DESLIZANTES
necesario
proporciona
Superficies conductores
circulares
Trayectoria de conducción
evita
Torsión de bobina
ayb
cuando
Bobina gira
de
Tensión
generada
Carga

15. Fem
inducida
tendrá
polaridad
en
-b
terminales
desarrollara
Corriente I
+a

16. MAGNITUD RELATIVA Y POLARIDAD DE LAS
TENSIONES 1
a) No existe líneas de flujo cortadas fem = 0
b) Se incrementa líneas de flujo cortadas por unidad de tiempo ,entonces
fem ≠ 0
c) Líneas de flujo cortadas por unidad de tiempo máximo , entonces
fem = máximo

17. MAGNITUD RELATIVA Y POLARIDAD DE LAS
TENSIONES 2
a) Polaridad de fem inducida y dirección de I permanecen iguales y fem = 0.
b) Fem se incrementa y cambia de polaridad para terminales a y b e inversión
de la dirección de corriente .
c) Fem = máximo pero polaridad se invierte de a y b .

18. FORMA DE ONDA SENOIDAL
Forma continua de fem
inducida ( eg ) y sus
respectivas polaridades .
*Si bobina sigue girando , fem generada se repetirá a intervalos
iguales de tiempo
* Forma de onda responde a tensión senoidal de corriente alterna (CA ).

19. TERMINOS BASICOS 1
i) FORMA DE ONDA
Trayectoria trazada por una cantidad
como fem en función de alguna
variable : Posición , tiempo,
grados,temperatura , etc.
ii) VALOR INSTANTANEO
Magnitud de forma de onda en cualquier instante
( Se denota por minúsculos : e1 , e2 )
iii) AMPLITUD O VALOR DE PICO
Valor máximo de una forma de onda ( Em )

20. TERMINOS BASICOS 2
iV) FORMA DE ONDA PERÍODICA
Se repite continuamente , después del mismo intervalo de tiempo.
V) PERIODO ( T )
Intervalo de tiempo entre repeticiones sucesivas de una forma de onda
periódica T1 = T2 = T3
Vi) CICLO
Porción de una forma de onda
contenido en un periodo .
Vii) FRECUENCIA ( f )
Número de ciclos producidos
en función del tiempo
f = 1/T  antes :ciclos por segundo ( cps ) , actual : hertz (Hz )

21. LA ONDA SENOIDAL
o Se adapta a las matemáticas y a
fenómenos físicos que se asocian
a los circuitos eléctricos .
o Forma de onda cuyo aspecto no se
afecta por las características de
•1 rad = 57,3°
respuesta de los elementos R , L y C
• 2πrad = 360°
• si la tensión que existe en un resistor , un inductor o un capacitor es
senoidal entonces la corriente resultante para cada uno tendrá
característica senoidal.

22. VALORES DE ABSCISA EN ONDA SENOIDAL.
ω = 2π = 2πf
T
ω = velocidad angular
(rad/s)
Si T => ω
Si f
=> ω

23. OBTENCIÓN DE ONDA SENOIDAL A
PARTIR DEL GIRO DE UN RADIO
VECTOR
La forma de onda senoidal
se deriva de la longitud de
proyeccion vertical de un
radio vector que gira con un
movimiento
circular
uniforme en torno a un
punto fijo

24. IDEM. OBTENCION DE ONDA
SENOIDAL

25. FORMATO GENERAL PARA LA
TENSIÓN O CORRIENTE SENOIDALES
ω=2π=
T
t
 = ωt
y = AmSen ωt
Si y = i , y = V
Am = Im o Am = Em
 i = Im Sen  = Im Senωt
e = Em Sen  = Em Senωt
* i y e son valores instantáneos de corriente o tensión en cualquier instante t.

26. RELACÍONES DE FASE
La relación de fase entre dos formas de ondas indica que una de ellas se
adelanta o atrasa ( en grados o radianes )
i) ONDA SENOIDAL
y = Am Sen (ωt ± θ )
Forma
de
onda
se
ha
desplazado en “θ” grados a
derecha o izquierda de 0°.
ii) ONDA COSENOIDAL .
y = Sen(ωt + 90° ) = Cos ωt
y = Sen(ωt – 90° )
*Curva coseno adelanta a la de seno en 90°
* 90° es el ángulo entre las dos formas de onda ( fuera de fase en 90° )

27. APLICACIONES DE SENO Y
COSENO EN RELACIÓN DE FASE
i) Sen(-  ) = -Sen 
ii) Cos (-  )= cos 
iii) –sen () = Sen ( ± 180°)
iV) –cos ( ) = cos ( ± 180° )
•Si e = - Em sen ωt
e = Em (-sen ωt ) = Em sen (ωt ± 180° )

28. FUNCIONES TRIGONOMETRICAS DE SUMA Y
DIFERENCIA DE DOS ANGULOS
i) Sen (∝ +β ) = sen ∝ cos β + cos∝ senβ
ii) cos (∝ +β ) = cos ∝ cos β - sen∝ senβ
iii) Sen (∝ - β ) = sen ∝ cos β - cos∝ senβ
iv) cos (∝ - β ) = cos ∝ cos β + sen∝ senβ

29. RELACION ENTRE FORMAS DE
ONDA ( ADELANTO Y RETRASO )
EJEMPLO 1 :
1° ¿ Cual es la relación de fase
entre las formas de ondas
senoidales que siguen?
v= 10 sen (ωt + 30°)
i = 5 sen (ωt + 70° )
Solucion:
i se adelanta a v en 40°
v se retrasa respecto a i en 40°

30. EJEMPLO 2:
v = 3 sen (ωt – 70° )
i = 2 sen (ωt – 40 ° )
Solución
i se adelanta a v en 30°
o v se retrasa sobre i en 30

31. VALOR PROMEDIO
Sea de corriente o tensión es el
valor indicado en un medidor de
corriente directa ( cd).
Ejemplo
Determine los valores promedio
( G ) de las formas de ondas
siguientes sobre un ciclo completo
i) G = +(3)(4)- (1)(4) = 1V
8

32. ii) G = -(10)(2) + (4)(2) – (2)(2) = - 1,6 V
10

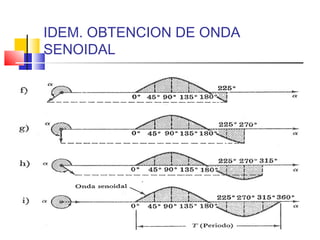
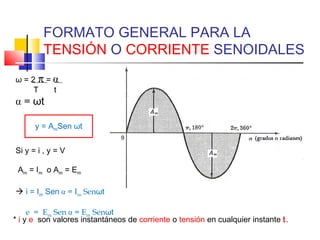
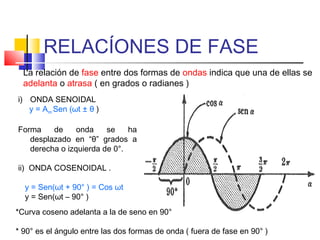
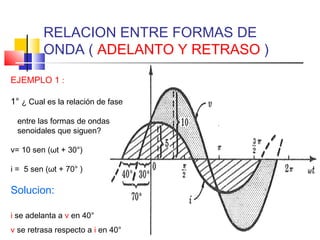
33. VALOR PROMEDIO
A1 =
= Am [ -cos ]
A1 = 2Am
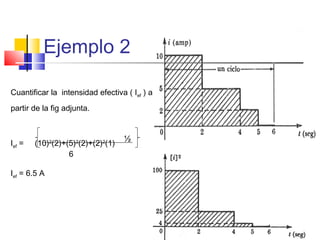
G = 2Am+(-2)(π)/ 2π
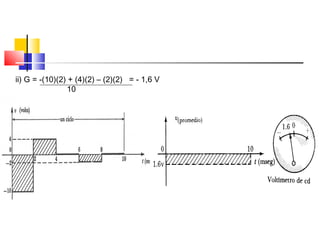
Luego : GT = (2)(10 – (2)(π) = 2,2V
2π

34. VALORES EFECTIVOS
La potencia alimentada por la corriente alterna(Ca) en cualquier instante es :
1° Pca = ( ica )2 R = (Im sen ωt)2 R= ( I2msen2 ωt)R
= I2m [ 1/2 (1-cos2 ωt ) ]R
*
I 2 mR
2
= I2mR - I2mRcos2 ωt
2
2
= potencia promedio alimentada por Ca

35. idem . Valores efectivos
2)Igualando la potencia promedio del generador de corriente
alterna(Ca)a la de la fuente de corriente directa (Cd) se tiene :
P(ca)= Pcd
I2m R = I2cd R
2

Icd = Im = 0,707 Im
√2
Además: Eef= 0.707 Em
Valor efectivo ( Icd = Ief )
valor efectivo ( Eef = Vef ).
El valor equivalente de cd o valor efectivo de una corriente
o tensión senoidal es 1/ de su valor máximo.

36. VALOR EFECTIVO Y VALOR DE
RAIZ CUADRADA MEDIA (rcm)
El valor efectivo de una cantidad cualquiera
trazada en función del tiempo es:
Esto indica que para encontrar valor efectivo es preciso elevar primero al cuadrado la función
i(t); después se determina el área bajo la curva mediante la integración. Luego se divide entre T
que es la longitud del ciclo o el periodo de la forma de onda, para obtener el valor promedio o
medio de la forma de onda elevada al cuadrado. Finalmente se procesa la raíz cuadrada del
valor medio. Este Procedimiento da otra designación para el valor efectivo: el valor de raíz
cuadrada media(rcm).

37. Ejemplo 1
Hallar el valor efectivo (vef) o el valor de
la raíz cuadrada media(rcm) de la
forma de onda de la fig. adjunta.
SOLUCIÓN:
Vef =
(9)(4)+(1)(4)
8
vef = 2.3V
½

38. Ejemplo 2
Cuantificar la intensidad efectiva ( Ief ) a
partir de la fig adjunta.
Ief =
(10)2(2)+(5)2(2)+(2)2(1)
6
Ief = 6.5 A
½

39. LA DERIVADA
Definido como índice de la variable (x) con respecto al tiempo (t)
Si X(t) = Xm sen ωt
dx = ωxm cos ωt
dt
dx = 2πfXm cos ωt
dt
Valor pico = 2πfXm
*Cuanto mas alta sea la frecuencia (f) tanto mas alto será el valor pico de la derivada

40. Derivada de una onda senoidal
es una onda cosenoidal.
* El valor pico de la onda cosenoidal
esta relacionada con la frecuencia
de la onda original
* Si f => dx
dt

41. RESPUESTA DE LOS ELEMENTOS R- L- C BÁSICOS
A LA CORRIENTE Y A LA TENSIÓN SENOIDALES
a) RESISTORES
SEGÚN LEY DE OHM:
i) i = v = Vm sen ωt
R
R
i = Im sen ωt
ii) V = iR = ( Imsen ωt )R
v= Vm sen ωt

42. Ejemplo 1
Dado V= 100 sen377 t en el resistor de
10 Ω hállese expresión senoidal de
corriente .
Solución
i= v = 100 sen377t
R 10
i = 10sen377t
* Para un elemento permanente resistivo
v y i están en fase .

43. Ejemplo 2
Para v= 25 sen( 377t + 60°)
hallar la expresión senoidal de
i si R = 10 Ω
Solución
i = v = 25 sen ( 377 t + 60° )
R 10
i = 2,5 sen( 377 t + 60° )

44. b) INDUCTORES
VL = L diL = L d( Imsen ωt )
dt
dt
VL= L (ωImcos ωt )
ó
VL = Vmsen ( ωt + 90° )
* Vm= ωL Im
* VL se adelanta a iL en 90°
*reactancia inductiva (X L)
XL = Vm = ωLIm
Im I m

45. Ejemplo 1
Hállese la expresión senoidal para la
tensión que existe en una bobina de
0,1 H Cuando pasa por el i = 10sen377t
Y bosquéjese las curvas de v e i .
Solución
Como en bobina v adelanta a i en 90º, entonces:
1° VL = Vmsen(ωt + 90 )
2°
XL = ωL =377(0,1) = 37,7Ω
Vm = Im XL = ImωL = 10(377)(0,1)= 377 V
3° como VL se adelanta a iL en 90°
⇒ V = 377sen(377t + 90°)

46. Ejemplo 2
Para i= 7sen(377t - 70)
y L = 0,1 H , hallar la expresión
senoidal de tensión en un inductor .
Solución
1° XL = ωL = ( 377 )(0,1)= 37,7Ω
2° Vm = ImXL=(7)(37,7)=264V
3° como VL adelanta a iL en 90°
VL = Vm sen(377t – 70 + 90°)
VL = 264sen(377t – 70 + 90°)

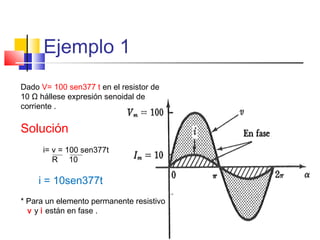
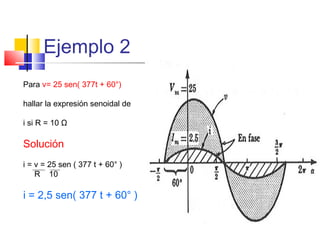
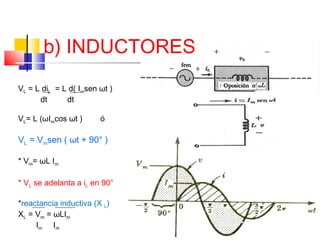
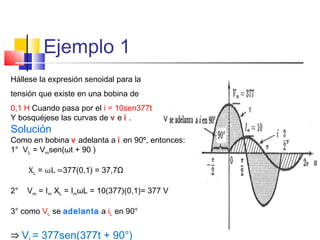
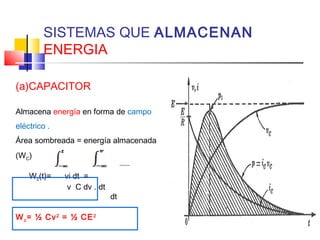
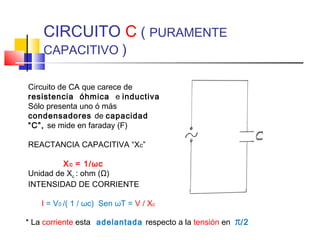
47. c) CAPACITOR
iC = C dvc
dt
ic = C d [Vmsenωt ]
dt
ic = C(ωVmcosωt)
Ó ic = Im sen (ωt + 90°)
* Im = ωcVm
* ic adelanta a vc en 90°
* reactancia capacitiva (Xc)
Xc = Vm = Vm = 1/ωC (ohm)

48. Ejemplo 1
Dado la tensión v = 30sen400t en el capacitor
de 1uf, determine la expresión senoidal para
la corriente
Solución
1° ic= Imsen(ωt + 90°)
2° Im = Vm = Vm =
30V
XC 1/ωc 1/(400x 1x 10-6)F
Im = 0,01 A
3° ic= 0,01sen (400t + 90°)

49. Ejemplo 2
Para v = 2 sen ( 10t + 60° ) en el capacitor
de 1uf, hállese la expresión senoidal para
la corriente
Solución
1° ic = Imsen (ωt + 90°)
2° Im = Vm = Vm =
2V
Xc 1/ωC 1/(10 x 1 x 10-6)F
Im = 20 x 10-6 A
3° ic = 20 x 10-6 sen ( 10t + 60° +90°)
i = 20 x 10-6sen ( 10t + 150°)

50. SISTEMAS QUE ALMACENAN
ENERGIA
(a)CAPACITOR
Almacena energía en forma de campo
eléctrico .
Área sombreada = energía almacenada
(WC)
Wc(t)=
vi dt =
v C dv . dt
W c = ½ Cv 2 = ½ CE 2
dt

51. Ejemplo 1
En el circuito adjunto, el capacitor de 20 mF, se
carga hasta 100V ¿Cuánto es la energía
almacenada por el capacitor y su voltaje para
t = 0 después de abrir el interruptor ?
Solución
1° Wc = ½ CE2
= ½ ( 20 mF )(100 V)2
Wc = 100 J
2° V(0) = 100 V

52. (b)INDUCTOR
Almacena energía en forma de
campo magnético.
Área sombreada = energía
almacenada(WC)
wc(t) =
=
EL= 1 L
2
(joule)
=
( L di )dt
dt

53. Ejemplo
Para circuito adjunto hállese energía
almacenada por el inductor
Solución
1° WL = ½ L Im2
2° Im = E/R = 15 v/5 Ω = 3 A
3° WL = ½ ( 6 mH) (3 A)2
WL= 27 x 10-3 J

54. Caso propuesto
Un “flasher” electrónico profesional tiene un capacitor de 1000uF
que se carga a 100 V, determine:
a) Energía almacenada por el capacitor.
b) La carga sobre el capacitor
c) La corriente promedio a través del flasher cuando el fotógrafo toma una placa
y el flash se enciende durante 0,5 milisegundos
d) La potencia suministrada al foco del aparato
e) El tiempo necesario para cargar el capacitor mediante una fuente de energía que
proporcione una corriente máxima de 10 mA, dado que después de tomar una
fotografía se debe recargar el dispositivo.