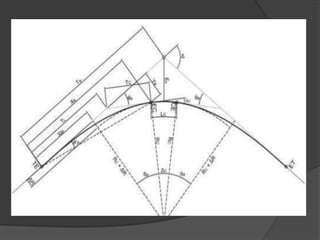
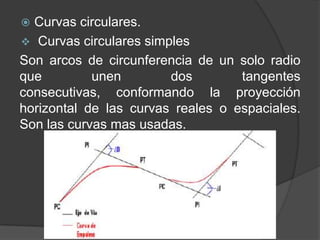
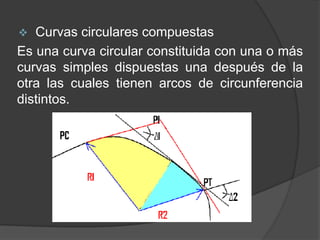
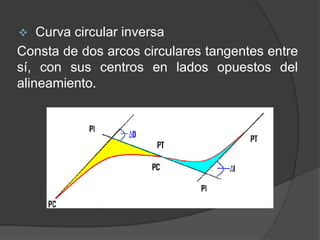
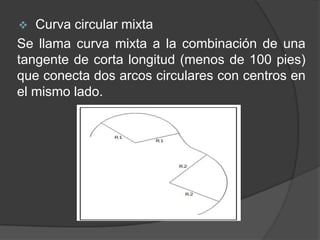
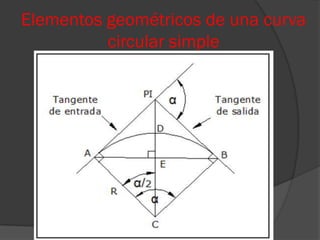
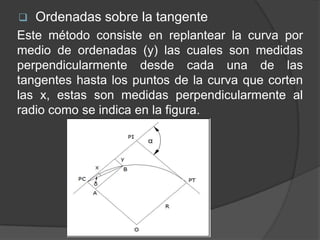
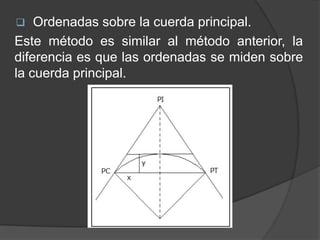
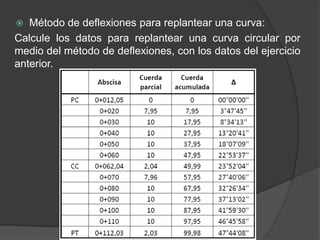
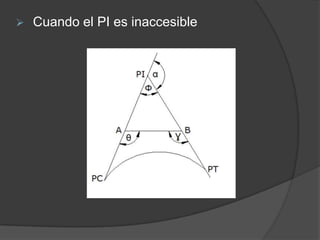
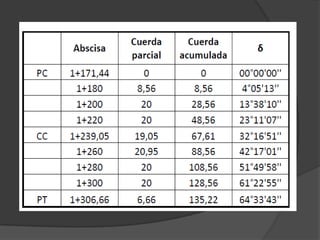
Este documento presenta información sobre curvas horizontales utilizadas en ingeniería civil. Explica que las curvas sirven para conectar tramos rectos y describe dos tipos principales de curvas: curvas espirales y curvas circulares. Define elementos geométricos clave de las curvas circulares como el punto de intersección, punto de inicio de la curva y punto final. Además, explica métodos comunes para replantear curvas en el campo como deflexiones angulares u ordenadas.

1. TOPOGRAFÍA APLICADA
Richar Javier Morocho Morocho
Escuela de ingeniería civil

2. CURVAS HORIZONTALES

3. Introducción
 Los tramos rectos (llamados tangentes) de
la mayor parte de las vías terrestres de
transporte, tales como carreteras, vías
férreas y tuberías, están conectados por
curvas en los planos tanto horizontal como
vertical.
 Las curvas usadas en planos horizontales
para conectar dos secciones
tangentes rectas se llaman curvas
horizontales. Se usan dos tipos: arcos
circulares y espirales.

4.  El alineamiento horizontal es la proyección
sobre un plano horizontal se su eje real o
espacial. Dicho eje horizontal está constituido
por una serie de tramos rectos denominados
tangentes, enlazados entre si por curvas.
 Las curvas compuestas, mixtas e inversas no
son apropiadas para las carreteras modernas
de alta velocidad, los sistemas de transporte
rápido; deberían evitarse si es posible. Sin
embargo, en ocasiones son necesarias, como
en terreno montañoso para evitar pendientes
excesivas o cortes y rellenos muy grandes.

5. Tipos
 Curvas espirales
Las espirales se usan en sistemas de vías
férreas y de tránsito rápido, ya que funcionan
como curvas de alivio. En las carreteras, rara
vez se usan las espirales porque los
conductores pueden dominar los cambios
direccionales bruscos. Las espirales se
utilizan para unir una tangente con una curva
circular, una tangente con otra tangente y una
curva circular con otra circular.

7.  Curvas circulares.
 Curvas circulares simples
Son arcos de circunferencia de un solo radio
que unen dos tangentes
consecutivas, conformando la proyección
horizontal de las curvas reales o espaciales.
Son las curvas mas usadas.

8.  Curvas circulares compuestas
Es una curva circular constituida con una o más
curvas simples dispuestas una después de la
otra las cuales tienen arcos de circunferencia
distintos.

9.  Curva circular inversa
Consta de dos arcos circulares tangentes entre
sí, con sus centros en lados opuestos del
alineamiento.

10.  Curva circular mixta
Se llama curva mixta a la combinación de una
tangente de corta longitud (menos de 100 pies)
que conecta dos arcos circulares con centros en
el mismo lado.

11. Elementos geométricos de una curva
circular simple

12. o PI : Punto de intersección
o PC (A) : Es el punto donde inicia la curva
o PT (B) : Punto donde termina la curva
o α : Angulo de deflexión o ángulo central
o API y PIB : Tangentes
o R, AB y AC : Radio del arco de la curva
o AB : Cuerda principal
o PID : External
o DE : Flecha
o AB : Longitud de la curva

13. Expresiones de cálculo
 Longitud de la tangente y external
 Grado de la curva
Por arco:
Por cuerda:

14.  Longitud de la curva
 Cuerda principal y flecha

15. Replanteo de curvas circulares
 Para replantear una curva circular lo
primero que se debe realizar es ubicar el
PI, una vez ubicado el PI se mide la
longitud de la tangente sobre el primer y
segundo alineamiento (tangente de
entrada y salida) para localizar el PC y PT.
A partir de estos puntos se puede
replantear la curva.
 Existen algunos métodos para replantear
una curva circular, los cuales son:

16.  Deflexiones angulares
Este método consiste en replantear todos los puntos
de la curva desde el PC midiendo los ángulos de
deflexión y cuerdas, el ángulo de deflexión es el
ángulo formado por la tangente y cada una de las
cuerdas que se miden desde el PC hasta los puntos
de la curva.
El método de deflexiones angulares es el más
utilizado.

17. A partir de la figura se obtiene la fórmula para
determinar la deflexión angular hacia cada uno de
los puntos.

18.  Ordenadas sobre la tangente
Este método consiste en replantear la curva por
medio de ordenadas (y) las cuales son medidas
perpendicularmente desde cada una de las
tangentes hasta los puntos de la curva que corten
las x, estas son medidas perpendicularmente al
radio como se indica en la figura.

19.  La fórmula sirve para
obtener diferentes valores de y a partir de
valores de x. Y de esta forma se localizan
todos los puntos de la curva.
 O también se pueden utilizar las fórmulas
siguientes para calcular x-y.

20.  Ordenadas sobre la cuerda principal.
Este método es similar al método anterior, la
diferencia es que las ordenadas se miden sobre
la cuerda principal.

21.  Por Coordenadas.
Este método consiste en replantear los
puntos de la curva mediante el uso de
coordenadas previamente calculadas y
desde cualquier punto escogido. Para
utilizar este método se debe contar
con el uso de una Estación Total o con
un GPS diferencial.

22. Casos especiales de replanteo
 En algunas ocasiones se presentan casos en
los que no se puede replantear una curva por
medio de los métodos mencionados
anteriormente, estos casos son:
-Cuando el Pi es inaccesible.
-Cuando el PI y el PC son inaccesibles.
-Cuando el PT es inaccesible.
-Replanteo de un punto cualquiera desde el PI.
-Cuando no se pueden observar todos los puntos
de la curva desde el PC por la presencia de
obstáculos.

23. EJEMPLOS DE CÁLCULO
 La abscisa del PI de una curva circular
es 0+078.07, el ángulo de deflexión es
igual a 95 grados 28 minutos y 15
segundos y el radio de la curva es
60m, calcule la abscisa del PC y del PT.

24.  Abscisa del PC
 Abscisa del PT

25.  Método de deflexiones para replantear una curva:
Calcule los datos para replantear una curva circular por
medio del método de deflexiones, con los datos del ejercicio
anterior.

26. En la primera columna se ubican las abscisas cada 10 m
desde el PC hasta el PT, el centro de la curva se calcula
dividiendo la longitud de la cuerda para dos mas la abscisa del
PC:
Luego se calculan las cuerdas parciales, restando las
abscisas:
Para determinar las cuerdas acumuladas se suman las
cuerdas parciales y por último se calculan las deflexiones
utilizando la fórmula:

27.  Abscisa 0+020

28.  Cuando el PI es inaccesible

30.  Por medio de la ley de senos:

33. GRACIAS POR
SU ATENCIÓN