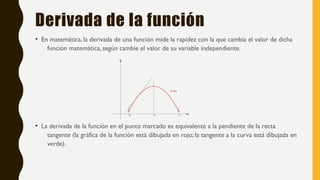
Este documento trata sobre derivadas. Explica que la derivada de una función mide la rapidez de cambio de la función cuando cambia su variable independiente, y que equivale a la pendiente de la tangente en un punto. También presenta ejemplos de cómo calcular derivadas de funciones como constantes, lineales, potenciales y raíces. Finalmente, incluye un ejercicio de sopa de letras con términos relacionados a derivadas.

1. DERIVADAS
J A S B L E Y S O L A N Y I C A S T R O P E R E Z
1 1 - 8

2. Derivada de la función
• En matemática, la derivada de una función mide la rapidez con la que cambia el valor de dicha
función matemática, según cambie el valor de su variable independiente.
• La derivada de la función en el punto marcado es equivalente a la pendiente de la recta
tangente (la gráfica de la función está dibujada en rojo; la tangente a la curva está dibujada en
verde).

3. La derivada, se calcula como el
límite de la rapidez de cambio
media de la función en cierto
intervalo, cuando el intervalo
considerado para la variable
independiente se torna cada
vez más pequeño.

4. ejemplo:
• Un ejemplo habitual aparece al estudiar el movimiento:
si una función representa la posición de un objeto con respecto al tiempo, su derivada es la
velocidad de dicho objeto.
Un avión que realice un vuelo transatlántico de 4500 km entre las 12:00 y las 18:00, viaja a una
velocidad media de 750 km/h. Sin embargo, puede estar viajando a velocidades mayores o
menores en distintos tramos de la ruta. En particular, si entre las 15:00 y las 15:30 recorre 400
km, su velocidad media en ese tramo es de 800 km/h. Para conocer su velocidad instantánea a las
15:20, por ejemplo, es necesario calcular la velocidad media en intervalos de tiempo cada vez
menores alrededor de esta hora: entre las 15:15 y las 15:25, entre las 15:19 y las 15:21.

5. Historia de la derivada
Los problemas típicos que dieron origen al cálculo infinitesimal, comenzaron a plantearse en la
época clásica de la antigua Grecia (siglo III a. C.), pero no se encontraron métodos sistemáticos
de resolución hasta diecinueve siglos después (en el siglo XVII por obra de Isaac Newton y
Gottfried Leibniz).
En lo que atañe a las derivadas existen dos conceptos de tipo geométrico que le dieron origen:
•
•
•
• El problema de la tangente a una curva (Apolonio de Perge)
• ElTeorema de los extremos: máximos y mínimos (Pierre de Fermat)
• En su conjunto dieron origen a lo que actualmente se conoce como cálculo diferencial.

6. Definiciones de deriva
• En terminología clásica, la diferenciación manifiesta el coeficiente en que una cantidad
{displaystyle y,} y, cambia a consecuencia de un cambio en otra cantidad {displaystyle x,} x,.
•
• En matemáticas, coeficiente es un factor multiplicativo que pertenece a cierto objeto como
una variable, un vector unitario, una función base, etc.
• En física, coeficiente es una expresión numérica que mediante alguna fórmula determina las
características o propiedades de un cuerpo.
• Por ejemplo, cuando se refiere a la gráfica de dos dimensiones de {displaystyle f} f, se considera
la derivada como la pendiente de la recta tangente del gráfico en el punto {displaystyle x} x. Se
puede aproximar la pendiente de esta tangente como el límite cuando la distancia entre los dos
puntos que determinan una recta secante tiende a cero, es decir, se transforma la recta secante
en una recta tangente.

7. • DATO:
Algunas funciones no tienen derivada en todos o en alguno de sus puntos. Por ejemplo, una
función no tiene derivada en los puntos en que se tiene una tangente vertical, una discontinuidad
o un punto anguloso.Afortunadamente, gran cantidad de las funciones que se consideran en las
aplicaciones son continuas y su gráfica es una curva suave, por lo que es susceptible de
derivación.
• Las funciones que son diferenciables (derivables si se habla en una sola variable), son
aproximables linealmente.
•

8. ejemplos: función derivada
para calcular la derivada de una función en un punto lo hemos hecho utilizando la definición de
la derivada:
•
•
• El resultado será una función que depende de x y para obtener la derivada en un punto en
concreto, sólo tenemos que sustituir la x por ese punto en la función derivada.
• No hay que confundir los conceptos de derivada de una función en un punto, que es un
número real, con una función derivada o simplemente derivada, que es una función.

9. ejemplo: Hallar la función derivada de la siguiente función:
•
•
1.Sustituimos f(x+h) y f(x) por sus funciones correspondientes:
•
•
2.Operamos y simplificamos términos:
•
•
3.Anulamos la h del numerador y del denominador y por último obtenemos el resultado:
•
•
4.Por tanto, la función derivada de la función anterior es:
•
•

10. Ejemplo: Derivada de una constante
• La derivada de una función constante es cero:
• Vamos a demostrarlo calculando su función derivada utilizando la definición:
•
•
• Por tanto, cada vez que la función sea una constante, la derivada será 0 y lo puedes poner
directamente.
•
• Por ejemplo: Calcular la derivada de la siguiente función:
•
• Como es una función constante, escribimos directamente su derivada:

11. ejemplo: Derivada de la función lineal
• La derivada de la función lineal es el número que multiplica a la x:
• Su demostración es la siguiente:
•
•
• Vamos a ver un ejemplo: Calcular al derivada de la siguiente función:
•
• Su derivada es igual al número que tiene delante la x:

12. Ejemplo: Derivada de la función
potencial
• Una función potencial es aquella donde la x está elevada a un exponente. Para calcular su
derivada, el exponente pasa a multiplicar a la x y se le resta 1 al exponente:
•
•
•
•
• Por ejemplo, calcular la derivada de:
• Pasamos el 2 multiplicando a la x y le restamos 1 al exponente:
•
•
•
•

13. Ejemplo: Derivada de una raíz
• La derivada de una raíz es un caso particular de la función potencial cuando el exponente es
fraccionario. La derivada de la raíz cuadrada de x es la siguiente:
•
•
• Si lo que tenemos es una función dentro de la raíz cuadrada, su derivada es:
•
•
• Por ejemplo:
• En el denominador, el índice pasa a multiplicar a la raíz y se le resta 1 al exponente del
radicando:
•
•

14. Sopa de letras

15. • -parábola – circunferencia - elipse – hipérbola – intervalos – valor absoluto –
inecuaciones – función – dominio – biyectivas – constante – cuadrática –
racional - asíntota