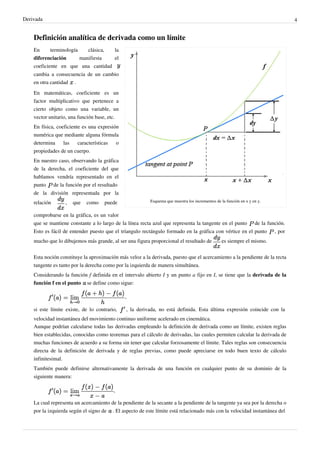
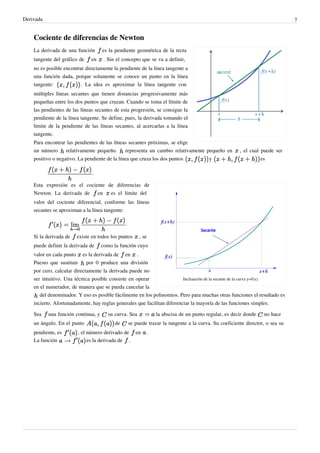
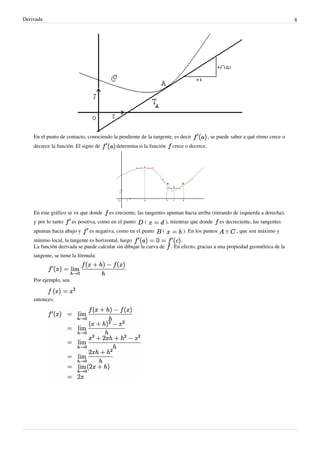
El documento explica los conceptos fundamentales de la derivada en matemáticas. La derivada mide el cambio en el valor de una función cuando cambia su variable independiente. Históricamente, la derivada surgió del estudio de tangentes a curvas y extremos de funciones. Hoy en día, la derivada es una herramienta crucial en campos como la física, química y economía para medir tasas de cambio.