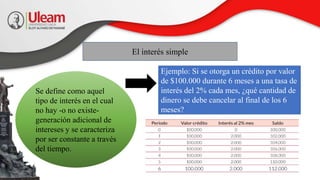
El documento enseña conceptos fundamentales de matemáticas financieras, centrándose en el valor del dinero en el tiempo y la importancia del interés compuesto en decisiones financieras. Se exploran temas como el interés simple, capitalización, y la necesidad de entender las tasas de interés para la inversión y financiación. Incluye ejemplos prácticos que ilustran cómo calcular el valor presente y futuro del dinero, así como el funcionamiento de los descuentos en préstamos.

1. UNIVERSIDAD LAICA ELOY ALFARO DE MANABÍ
CAMPUS PICHINCHA
CARRERA DE AGRONEGOCIOS
SEGUNDO SEMESTRE
MATEMÁTICAS FINANCIERA
UNIDAD 1. INTRODUCCIÓN A LA MATEMÁTICA
FINANCIERA – VALOR DEL DINERO EN EL TIEMPO.
UNIDAD 2. DEFINICIÓN DE INTERÉS COMPUESTO -
CAPITALIZACIONES.
UNIDAD 3. ACUMULACIÓN DE INTERÉS Y TASAS DE
INTERÉS. VALOR PRESENTE Y ECUACIONES.
UNIDAD 4. TASAS DE INTERÉS Y DISTRIBUCIÓN
NORMAL. Ing. Alfredo Vera Giler, MSc.
DOCENTE

2. UNIDAD 1. INTRODUCCIÓN A LA MATEMÁTICA FINANCIERA – VALOR DEL
DINERO EN EL TIEMPO.

3. Las matemáticas financieras son un importante recurso para la comprensión de las finanzas, ya que son la base
para entender el concepto del valor del dinero en el tiempo. Su conocimiento aporta a las decisiones que se
deben tomar en el ámbito financiero, particularmente, en relación con las actividades de financiación e
inversión.
El usuario, el analista, el gerente financiero, deben conocer los rendimientos de las inversiones y calcular el
valor de las cuotas para tomar decisiones de financiación; deben entender, además, cómo afectan las tasas de
interés a la inversión, entre otros temas, para los cuales las matemáticas financieras son una herramienta
imprescindible.
Introducción, Capitalización Y Descuento Simple Y Sus
Factores.
Introducción

4. Valor del dinero en el tiempo
Según Escobar (2020) El dinero es una
mercancía que permite el intercambio con
otras mercancías cuya característica
principal es tener precio o valor. De
acuerdo con esto, el dinero tiene un valor
que está determinado por su
denominación, es decir, un billete de
$10.000 permite adquirir otras mercancías
que poseen el mismo o menor valor.
Cuando se va a obtener una mercancía, se acude al lugar
apropiado para su adquisición; por ejemplo, si se necesita
adquirir una camisa, se asiste al almacén de ropa y se
entrega una cantidad de dinero necesaria que permita el
intercambio por una camisa. Lo anterior significa que al
existir un precio por las mercancías, se da la posibilidad de
su intercambio.
Ahora bien, ¿cuál es, entonces, el
precio del dinero?

5. El precio del dinero es la tasa de interés
que se paga por su uso.
Los precios varían permanentemente debido a
los efectos de la oferta y la demanda.
En la medida que exista mayor demanda por el
crédito, las tasas de interés comienzan a
aumentar; cuando hay poco apetito de crédito
por parte de las personas naturales y las
empresas, las tasas de interés tienden a
disminuir.
Para resumir, el valor del dinero
en el tiempo consiste en obtener
una tasa de interés, ya sea por
medio de un intermediario
financiero o un negocio o
empresa que supere la tasa de
inflación.

6. La línea de tiempo
Como su propio nombre lo indica, es una línea en la
cual se puede determinar el valor que tiene el
dinero en el tiempo (Arias, 2005), haciendo uso de
las variables con las que operan las matemáticas
financieras, que son:
• Valor presente (VP)
• Valor futuro (VF)
• Tasa de interés (I)
• Tiempo (N)
Y que, gráficamente, se puede representar de la
siguiente forma:

7. El interés simple
Se define como aquel
tipo de interés en el cual
no hay -o no existe-
generación adicional de
intereses y se caracteriza
por ser constante a través
del tiempo.
Ejemplo: Si se otorga un crédito por valor
de $100.000 durante 6 meses a una tasa de
interés del 2% cada mes, ¿qué cantidad de
dinero se debe cancelar al final de los 6
meses?

8. Teniendo en cuenta esto, se establece
que en el interés simple nunca hay
recapitalización de intereses; o sea, estos
no se aplican a los intereses que va
generando el crédito o el ahorro, sino
que se suman al final de la operación. El
ejemplo anterior expresado en la línea de
tiempo se muestra de la siguiente forma:
El interés simple
NOTA: El interés simple es un tipo de interés utilizado en créditos denominados como el “gota a
gota”, “paga diario”, entre otros. Es un tipo de interés informal.

9. Fórmulas del interés simple
Para establecer los diferentes
valores bajo el esquema del interés
simple se proponen las siguientes
fórmulas:

10. Ejemplo 1: Un crédito por valor de $10.000.000
será cancelado dentro de 1 año y fue otorgado a una
tasa de interés del 1,5% mensual. ¿Cuánto dinero se
debe cancelar al final del periodo?
EJEMPLOS
Obsérvese que el tiempo (N) está
expresado en términos de años; mientras
que la tasa de interés (I), en meses. Para
resolver el ejercicio, el tiempo (N) y la tasa
de interés (I), deben estar expresados en la
misma periodicidad (la tasa de interés
debe permanecer constante). De modo que
debe cambiarse el tiempo para que sea
igual a la base de tiempo en la que está
expresada la tasa de interés. En el ejemplo,
el tiempo (N) pasa de ser 1 año a 12 meses.

11. Ejemplo 2: En 6 meses un empresario requiere
la suma de $5.000.000 para invertirlos en su
empresa. ¿Cuánto dinero debe tener disponible
hoy en una cuenta que le reconoce una tasa de
interés del 0,4% mensual de interés simple?

12. Ejemplo 3: Un inversionista adquirió hace 2 años un
bien por valor de $8.200.000, el cual puede vender hoy
en $9.320.000. ¿Qué rentabilidad anual y mensual de
interés simple se está generando en este negocio?

13. Ejemplo 4: ¿En cuánto tiempo una inversión de
$200.000 se puede convertir en $300.000, si la
tasa de interés que se reconoce sobre la
inversión es del 5 % anual de interés simple?

14. Ejemplo 5: A un comerciante le prestaron $8.000.000 el
10 de marzo. ¿Cuánto dinero debe cancelar el 20 de junio
del mismo año, si la tasa de interés es del 14 % anual de
interés simple?

15. Como se ha mencionado anteriormente,
tanto la periodicidad de los intereses (I)
como la del tiempo (N) deben coincidir
en sus términos. En el ejemplo se debe
determinar el número de años que hay
entre las dos fechas mencionadas (10 de
marzo y 20 de junio), de tal forma que
el tiempo y la tasa de interés queden
expresados en la misma periodicidad.
Se tiene entonces:
Para determinar el número de años entre las fechas,
se realiza una regla de 3 simple de la siguiente
forma:

16. Descuento simple
Cuando se obtiene un préstamo por una cantidad C, se extiende un pagaré que es
una promesa de pago, el cual ampara una cantidad de dinero con o sin interés, en
una fecha determinada por el deudor y el acreedor o dueño del documento, este
documento se suscribe a favor del acreedor.
El descuento a los documentos se puede realizar de dos maneras: el llamado
descuento comercial o bancario y el descuento real o justo. El descuento
comercial o bancario o simplemente descuento, consiste en cobrar el interés en el
momento en que se realiza el préstamo; en otras palabras, se cobran los intereses
por anticipado y no hasta la fecha de vencimiento. Este se calcula considerando
el valor final del documento (valor futuro del capital).

17. Descuento (D ) Es la cantidad descontada, en un periodo (n), con
una tasa de descuento simple (d ) de una cantidad de dinero
solicitado. El monto o valor final del documento, es la cantidad
solicitada en el préstamo, pero esta nunca se recibe.
D = Mnd
Ejemplo 1. ¿Cuál es el descuento que se hace a un
préstamo de $4 800.00, a un plazo de siete meses, con una
tasa de descuento simple de 12% anual?
Datos:
M= $4 800 00
N= 7 meses
d= 12% anual
d= 0,12/12= 0,01
D= ?
D= Mnd
D= 4 800 00 (7) (0,01)
D= $336 00