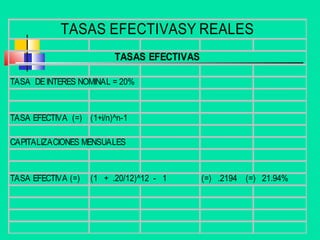
Este documento trata sobre conceptos básicos de matemáticas financieras y el valor del dinero en el tiempo. Explica el interés simple y compuesto, los periodos de tiempo, pagos, valor presente y futuro. También define tasas de interés nominal, anualizada, compuesta, flotante y real.

1. Matemáticas financieras y valor del dinero en el tiempo

2. Interés Interés es un cargo por pedir dinero prestado o el rendimiento que se recibe por ahorrarlo, normalmente se establece como un porcentaje de la cantidad prestada durante un periodo especifico.

3. Valores a conocer (a) la Tasa de Interés, (b) el plazo, número de periodos, (c) los pagos a realizar o recibir, (d) el valor presente, y (e) el valor futuro

4. Interés Interés Simple : El interés simple se calcula únicamente sobre la cantidad originalmente prestada o invertida. Es pues el rendimiento obtenido sobre el principal durante un periodo de tiempo. Interés Compuesto . El interés compuesto es calculado durante cada periodo sobre el monto original prestado o invertido mas los intereses no pagados y acumulados a la fecha, es decir se considera que el interés genera intereses sobre sí mismo.

5. Tiempo Los periodos son intervalos de tiempo igualmente espaciados entre sí. Un periodo puede corresponder a cualquier denominación en términos de tiempo

6. Pagos Los pagos son una serie de flujos de efectivo iguales y espaciados en la misma unidad de tiempo, para los cálculos de Valor del dinero en el tiempo, los pagos representan todos las entradas (flujos positivos) o todas las salidas (flujos negativos).

7. Valor presente El valor presente ( M$ ) de una cantidad futura ( F$ ) descontado a una tasa de interés ( i% ) durante n periodos es: P = (1+ i) n 1

8. Valor Futuro Es el valor que adquiere el capital al término de un periodo determinado por ocurrir Un flujo de efectivo ( P$ ) en el momento actual ( momento 0 ) gana intereses a una tasa de i% por periodo durante n periodos y tiene un valor futuro de: F = P(1 + i) n ,

13. VALOR DEL DINERO EN EL TIEMPO. REGLAS BASICAS Ante dos capitales de igual cuantía en distintos momentos, se preferirá aquél que sea más cercano Ante dos capitales en el mismo momento pero de distinto importe, se preferirá aquel de importe más elevado

14. Valor del dinero en el tiempo una misma cantidad de dinero en dos unidades de tiempo diferentes, son diferentes Capacidad de generar valor Perdida del poder adquisitivo

15. VALOR DEL DINERO EN EL TIEMPO Para poder comparar dos capitales en distintos instantes, hay que hallar el equivalente de los mismos en un mismo momento

16. Ejemplo: ¿Qué es preferible: disponer de 2 millones de pesos dentro de 1 año o de 4 millones dentro de 5 años?. No hay respuesta absoluta! ¿Valor Presente o Valor Futuro?

17. Valor del Dinero en el tiempo VALOR PRESENTE VALOR FUTURO COMPONER inflacionar DESCONTAR deflacionar

18. Valor presente de una serie de pagos P = F1/(1+i)1 + F2/(1+i)2 + … + Fn/(1+i)n. Excell =VNA(E4,D6:D17) Celda de la tasa de interés Valores futuros Inglés NPV? FE t (1 + i ) t P= ∑ t=1 n

19. Valor presente de una anualidad P = A/(1+i)1 + A/(1+i)2 + … + A/(1+i)n. (a) Excell =VA(E4,C17,F5) Tasa de interés Flujos o pagos supone que son negativos P = A 1 - 1 (1 + i ) n i

20. Valor Futuro de una anualidad F = A(1 + i) n-1 + A(1 + i) n-2 + … + A(1+ i) 1 + A (1 + i) n - 1 i F = A

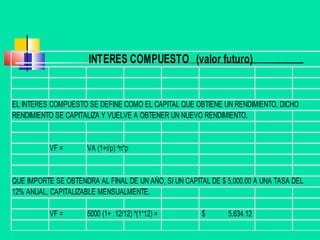
21. Valor Futuro de una anualidad Si usted ahorra una cantidad igual de $10,000 cada año, durante 10 años. ¿Cuál sería la cantidad que tendría al término de los 10 años, si los pudiera invertir a una tasa del 10%? (suponga que los pagos se hacen al final de cada uno de los años) Valor Futuro = 10,000 [1.10 10 - 1] / 0.10 = 159,374.25

22. Tasas de Interés Tasa de Interés, es la representación porcentual del costo o beneficio que habrá que cubrir o cobrar por el uso de los recursos. Normalmente y a menos que se indique explícitamente lo contrario, las tasas de interés se expresan en términos anuales. Tasa de Interés Nominal, es la tasa expresada en términos contractuales, representa la tasa de interés base sobre la cual se obliga el uso del dinero

23. Tasas de Interés Tasa de Interés Anualizada. Cuando una tasa de interés esta expresada en términos diferentes a los de un año, y se convierte en su equivalente a interés simple para un año, por ejemplo una tasa del 1% mensual, se convertiría en una tasa anualizada del 12%. Tasa anualizada = (i / n) * 360 Donde: i = tasa expresada n = número de días de la tasa En este caso se usa por convención el plazo de una año a 360 días, aunque en sentido estricto debería expresarse a 365 días.

24. Tasas de Interés Tasa de Interés Anual Compuesta. Es cuando una tasa de interés esta expresada en términos diferentes a los de un año, y se convierte a su equivalente a interés compuesto para un año, por ejemplo una tasa de interés del 1% mensual es igual a una tasa de interés anual compuesta del 12.69% Tasa anual compuesta = (1 + (i/360))360/n - 1

25. Tasas de Interés Tasa de Interés Pasiva, es la tasa de interés que una institución financiera debe pagar por el dinero que recibe en préstamo, se llama pasiva dado que desde el punto de vista del balance el préstamo representa un pasivo para la institución. Tasa de Interés Activa, es la tasa de interés que una institución financiera cobra por el dinero que otorga en préstamo, se llama activa dado que desde el punto de vista del balance el préstamo representa un activo para la institución, a la diferencia entre las tasa activa y pasiva se le conoce como margen de intermediación.

26. Tasas de Interés Tasa de Interés Flotante, es cuando la tasa prevé su adecuación a la fluctuación que se da en el mercado sobre las tasas de interés. En este sentido la tasa de adecua a las condiciones económicas que rigen en un momento dado, por lo tanto puede subir o bajar en función de dichas condiciones. Tasa de Descuento. Tasa que permite obtener el descuento de un documento en función de su valor nominal, con el propósito de determinar su valor antes del vencimiento.

27. Tasas de Interés Tasa de Interés Real. Es la tasa de interés que se obtiene una vez descontada la inflación observada durante el periodo equivalente de la tasa de interés, cuando la inflación es mayor que la tasa de interés se habla de una tasa interés real negativa, y cuando la tasa de interés es mayor a la inflación se habla de una tasa positiva.

30. Ejemplos

31. Ejemplo 1 Dell de México ofrece la siguiente oferta: Inspiron 1150 Promo 12/0 Su Precio $16,029.35 Precio en Pesos Mexicanos. El Precio incluye Flete y Impuestos de Importación. No incluye el 15% de IVA.

32. Ejemplo 1 Inspiron 1150 en Español SuPrecio $12,815.68* Precio en Pesos Mexicanos. El Precio incluye Flete y Impuestos de Importación. No incluye el 15% de IVA.

33. Ejemplo 2 Le debes a banamex $ 50,000 en tu tarjeta de crédito. La tasa de interés actual es 3.1 % mensual te parece que el cobro es excesivo y vas a la caja popular a pedir un crédito, para liquidar el saldo en el banco

34. Ejemplo 2 La caja te ofrece lo siguiente: Tasa de interés del 1.95% mensual Crédito a 10 meses Te prestan 5 tantos de ahorro congelado El pago debe ser quincenal ¿Cuál de los dos créditos te conviene más?