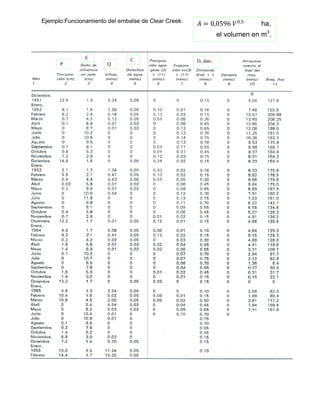
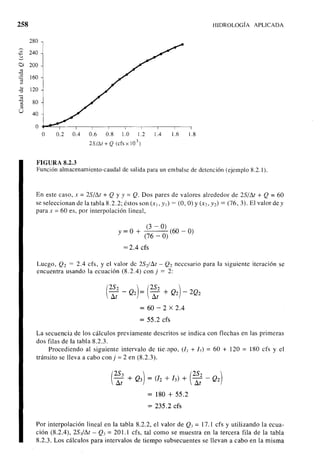
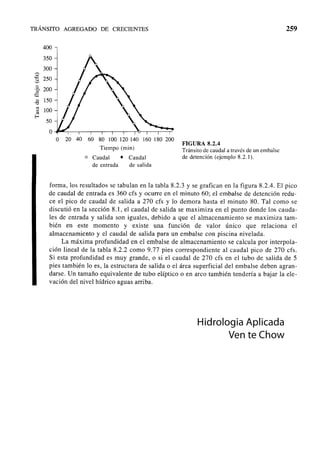
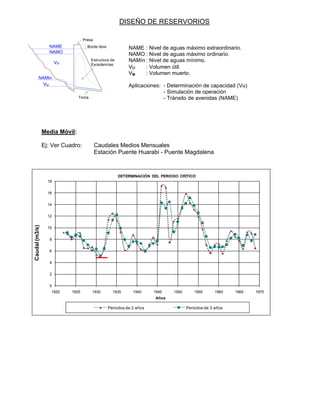
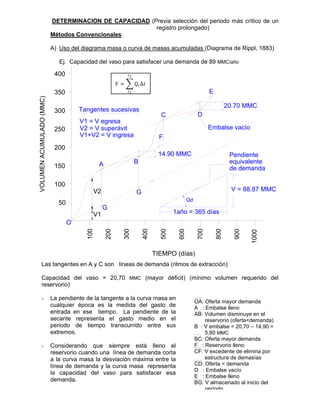
Este documento presenta información sobre el diseño de reservorios, incluyendo definiciones como el nivel máximo extraordinario de aguas y el nivel mínimo de aguas. Explica cómo determinar la capacidad y simular la operación mediante el uso de la media móvil de caudales históricos. Finalmente, describe los métodos convencionales para determinar la capacidad requerida, como el diagrama de masas acumuladas de Rippl, utilizando el período crítico más severo de registros prolongados.

1. DISEÑO DE RESERVORIOS
NAME : Nivel de aguas máximo extraordinario.
NAMO : Nivel de aguas máximo ordinario.
NAMín : Nivel de aguas mínimo.
V : Volumen útil.
VM : Volumen muerto.
Aplicaciones: - Determinación de capacidad (Vu)
- Simulación de operación
- Tránsito de avenidas (NAME)
Media Móvil:
Ej: Ver Cuadro: Caudales Medios Mensuales
Estación Puente Huarabi - Puente Magdalena
0
2
4
6
8
10
12
14
16
18
1920 1925 1930 1935 1940 1945 1950 1955 1960 1965 1970
Caudal
(m3/s)
Años
DETERMINACIÓN DEL PERIODO CRÍTICO
Periodos de 2 años Periodos de 3 años
NAME
NAMO
V
NAMin
VM
Presa
Borde libre
Estructura de
Excedencias
Toma

2. Caudales Medios Mensuales, m3
/s: Estación Puente Huarabí - Puente Magdalena
Año Ene Feb Mar Abr May Jun Jul Ago Set Oct Nov Dic
Media
Móvil (1)
Media
Móvil (2)
Media
Móvil (3)
1921 8,27 25,91 42,65 14,08 4,93 2,54 2,56 1,92 1,92 2,11 1,88 4,82 9,47
1922 7,24 25,99 36,43 14,77 5,33 3,98 2,21 1,77 1,86 1,91 2,15 3,87 8,96 9,21
1923 13,27 16,36 35,45 17,56 4,44 3,90 2,61 1,77 1,79 1,81 2,15 6,35 8,96 8,96 9,13
1924 7,96 18,81 30,58 9,38 2,72 2,82 2,62 1,87 1,47 1,23 1,48 4,78 7,14 8,05 8,35
1925 16,00 22,80 30,98 14,86 13,38 4,64 3,13 2,43 1,72 1,67 1,73 7,41 10,06 8,60 8,72
1926 8,51 23,97 14,65 23,58 7,19 2,80 2,57 2,15 2,54 2,70 3,93 3,88 8,21 9,13 8,47
1927 10,20 8,91 12,34 7,41 4,77 2,71 2,50 2,03 1,79 2,34 1,63 2,22 4,90 6,56 7,72
1928 6,68 17,30 28,57 17,64 8,17 4,13 3,00 2,64 1,88 2,34 1,68 2,77 8,07 6,49 7,06
1929 3,59 5,91 20,25 11,44 5,31 3,38 2,56 2,04 1,24 1,60 2,11 4,06 5,29 6,68 6,09
1930 7,19 14,96 18,04 6,41 5,78 2,80 2,43 1,89 1,53 1,52 2,35 1,85 5,56 5,43 6,31
1931 4,24 3,56 16,42 11,65 3,07 1,95 1,98 1,61 1,29 1,31 1,22 5,48 4,48 5,02 5,11
1932 16,16 36,32 19,16 13,69 4,91 3,90 4,44 2,44 1,26 1,10 2,28 1,42 8,92 6,70 6,32
1933 17,76 34,66 45,52 41,66 6,31 5,81 3,98 2,77 1,53 1,74 1,34 2,91 13,83 11,38 9,08
1934 23,43 23,07 46,00 10,17 6,91 7,36 6,72 4,08 2,15 1,24 1,19 1,21 11,13 12,48 11,29
1935 12,05 22,07 59,18 15,28 5,89 2,73 2,15 1,64 1,32 1,02 1,06 14,38 11,56 11,35 12,17
1936 28,05 20,90 13,86 7,21 4,03 2,65 1,64 1,71 1,33 1,07 1,05 0,96 7,04 9,30 9,91
1937 5,50 9,11 22,53 7,80 4,77 3,04 1,82 1,26 0,86 0,69 0,81 3,99 5,18 6,11 7,93
1938 6,20 32,25 22,35 19,27 5,90 3,76 2,94 1,57 1,07 0,88 0,95 1,18 8,19 6,69 6,80
1939 4,97 23,03 47,18 19,01 3,65 3,64 1,59 1,49 1,15 1,18 1,07 3,75 9,31 8,75 7,56
1940 15,02 7,80 16,00 9,02 3,87 2,65 1,44 1,15 1,10 1,87 2,29 1,43 5,30 7,31 7,60
1941 11,16 22,95 33,01 3,81 2,15 1,42 1,19 1,62 2,05 2,09 1,91 3,80 7,26 6,28 7,29
1942 8,11 18,36 13,20 6,19 3,36 1,73 1,57 2,15 1,82 1,87 1,71 1,85 5,16 6,21 5,91
1943 7,37 36,61 23,03 14,84 3,99 2,05 1,59 2,06 2,06 1,97 2,09 4,14 8,48 6,82 6,97
1944 10,67 27,28 36,19 7,43 3,93 2,02 1,78 2,00 2,14 2,03 1,81 1,70 8,25 8,37 7,30
1945 6,60 12,14 14,54 6,98 3,15 1,36 1,11 1,26 1,79 1,55 2,00 20,68 6,10 7,17 7,61
1946 62,84 57,25 55,10 70,57 69,60 8,43 1,82 1,68 1,68 1,74 2,70 7,81 28,44 17,27 14,26
1947 11,87 9,91 19,95 6,41 2,86 0,94 0,68 1,69 2,35 3,38 1,74 3,63 5,45 16,94 13,33
1948 22,20 21,47 23,44 17,49 5,33 3,53 2,55 1,84 1,81 3,66 7,24 4,23 9,57 7,51 14,48
1949 12,41 13,39 66,45 40,17 3,60 2,85 1,23 2,23 2,93 2,98 3,03 1,02 12,69 11,13 9,24
1950 15,64 36,64 19,10 12,81 7,75 4,07 3,97 3,42 3,21 3,34 2,43 15,15 10,63 11,66 10,96
1951 35,65 50,00 57,35 22,92 2,48 1,96 2,05 1,72 2,74 2,74 8,83 12,19 16,72 13,67 13,35
1952 34,61 50,99 40,85 31,32 6,03 4,22 3,95 2,27 1,21 1,35 1,41 2,32 15,04 15,88 14,13
1953 8,02 53,14 43,96 21,39 7,44 4,51 3,17 1,66 1,32 2,23 6,21 10,19 13,60 14,32 15,12
1954 19,40 30,01 37,60 10,25 12,38 7,52 5,79 5,29 6,34 6,13 6,37 5,72 12,73 13,17 13,79
1955 15,53 22,87 47,88 24,31 4,73 4,11 3,53 1,72 2,27 1,74 3,10 3,57 11,28 12,01 12,54
1956 2,55 28,31 34,17 19,05 6,55 2,43 1,01 1,02 1,12 1,35 1,17 1,34 8,34 9,81 10,78
1957 3,20 18,51 16,90 19,80 4,93 1,40 0,51 0,65 0,70 0,90 1,08 1,19 5,81 7,08 8,48
1958 4,49 17,51 20,56 5,74 3,67 2,62 1,89 1,94 1,68 1,84 1,76 1,76 5,46 5,63 6,54
1959 1,71 35,01 35,42 8,31 2,63 1,49 1,34 1,32 1,30 2,04 3,38 11,43 8,78 7,12 6,68
1960 13,43 19,74 17,95 5,59 1,47 1,58 1,40 1,12 1,04 1,27 1,20 1,34 5,59 7,19 6,61
1961 9,85 17,98 14,85 13,80 2,92 1,17 0,89 0,78 0,76 1,00 1,85 1,43 5,61 5,60 6,66
1962 15,89 30,51 30,44 25,58 3,04 1,69 0,93 0,73 0,65 2,61 2,79 3,47 9,86 7,73 7,02
1963 14,42 25,20 25,90 14,52 2,41 1,29 0,85 0,76 0,65 1,64 4,81 15,98 9,04 9,45 8,17
1964 8,66 19,05 29,55 19,04 4,01 1,92 0,89 0,78 1,01 1,79 4,47 3,11 7,86 8,45 8,92
1965 4,53 19,84 52,52 5,75 2,22 0,85 0,80 0,54 1,05 1,54 1,83 2,66 7,84 7,85 8,25
1966 11,84 7,05 14,20 3,17 1,18 0,77 0,45 0,27 0,99 4,88 4,42 10,32 4,96 6,40 6,89
1967 17,34 56,19 59,60 12,86 3,44 1,61 1,13 0,94 1,17 3,16 2,28 3,35 13,59 9,28 8,80
1968 7,57 9,27 14,17 9,85 1,66 1,25 0,72 0,49 0,70 2,54 2,57 3,59 4,53 9,06 7,69
1969 3,74 9,14 21,65 14,72 2,02 0,72 0,52 0,43 0,98 3,38 2,65 41,05 8,42 6,47 8,85
Considerando como periodo crítico el periodo de 3 años (1929 - 1931):

3. 50
100
200
150
100
300
200
400
400
350
300
250
500
600
800
700
1000
900
14.90 MMC
20.70 MMC
A B
C D
E
1año = 365 días
Embalse vacío
Pendiente
equivalente
de demanda
V = 88.87 MMC
O
F
Qd
TIEMPO (días)
VOLUMEN
ACUMULADO
(MMC)
V2
V1
G
G
V1 = V egresa
V1+V2 = V ingresa
V2 = V superávit
Tangentes sucesivas
DETERMINACION DE CAPACIDAD (Previa selección del periodo más crítico de un
registro prolongado)
Métodos Convencionales
A) Uso del diagrama masa o curva de masas acumuladas (Diagrama de Rippl, 1883)
Ej. Capacidad del vaso para satisfacer una demanda de 89 MMC/año
Las tangentes en A y C son líneas de demanda (ritmos de extracción)
Capacidad del vaso = 20,70 MMC (mayor déficit) (mínimo volumen requerido del
reservorio)
- La pendiente de la tangente a la curva masa en
cualquier época es la medida del gasto de
entrada en ese tiempo. La pendiente de la
secante representa el gasto medio en el
periodo de tiempo transcurrido entre sus
extremos.
- Considerando que siempre está lleno el
reservorio cuando una línea de demanda corta
a la curva masa la desviación máxima entre la
línea de demanda y la curva masa representa
la capacidad del vaso para satisfacer esa
demanda.
OA: Oferta mayor demanda
A : Embalse lleno
AB: Volumen disminuye en el
reservorio (oferta<demanda)
B : V embalse = 20,70 – 14,90 =
5,80 MMC
BC: Oferta mayor demanda
F : Reservorio lleno
CF: V excedente de elimina por
estructura de demasías
CD: Oferta < demanda
D : Embalse vacío
E : Embalse lleno
BG: V almacenado al inicio del
período
∆
2
1

4. REGULACION OPTIMA: Se logra una regulación óptima con el aprovechamiento
máximo de las aguas del río al regular un caudal igual al caudal medio del periodo.
Ej: Se ha dibujado la curva masa para los tres años de mayor irregularidad dentro del
periodo de registro.
VOLUMEN ÚTIL RECOMENDADO
DETERMINACION DEL CAUDAL REGULADO PARA UNA CAPACIDAD DE
ALMACENAMIENTO DADA (RENDIMIENTO)
En este caso las tangentes se
trazan en los puntos altos de la
curva masa (M,N) en forma tal que
su desviación máxima no exceda la
capacidad del vaso (EF). La
pendiente de las tangentes es el
rendimiento y la pendiente de la
línea más plana es el rendimiento
firme.
En el ej.: QD = 70 MMC/año
Una línea de demanda debe cortar la curva masa cuando se prolonga, en caso de no
hacerlo el vaso no se vuelve a llenar.
Q
A
C
U
R
T
S
D
B
1977 1978 1979
meses
V acumulado
MMC
QU : Capacidad mínima del embalse
ST=RU=AC : Vol que hay que tener
almacenado antes que empiece
el periodo.
QR : Vol que hay que almacenar
durante el periodo
Q : capacidad colmada del reservorio
T : reservorio vacío
.
V
recomendable
V
QD
% del V de escurrimiento medio
50
100
A
La regulación óptima resulta
costosa, por lo tanto un reservorio
que aproveche la máxima
cantidad de agua posible tendría
que tener el V correspondiente al
punto A (consideración con
criterio hidrológico solamente).
100
200
300
1932 1933 1934 1935
M
E
F
N
E
F
M
N
120
70 MMC/año
1 Año
Ej : Vu = 50 MMC = EF
V acum.
Meses

5. B) ANALISIS PICO SECUENCIAL (Especialmente para demanda variable) (1963) (Curva
Masa Residual) (Diferencia entre oferta y demanda acumulada vs. tiempo)
Para un embalse único:
A = almacenamiento requerido
para cubrir el déficit.
AM = Almacenamiento máximo
Se busca los almacenamientos
requeridos para el registro
histórico y se escoge el mayor
valor.
RANGO = Diferencia entre las
ordenadas máximas y mínimas
de la curva residual para el
periodo dado.
ANALISIS DEL RANGO PROPUESTO POR HURST (1951)
73
,
0
2
N
S
R 






El exponente en la práctica varía entre 0,46 y 0,96, teóricamente para una distribución
normal varía entre 0,5 y 0,7.
METODO ANALITICO PARA HALLAR LA CAPACIDAD:
Ej.: Encontrar el volumen de almacenamiento requerido para mantener una demanda
constante de 1050 m3
por y por km2
de cuenca, si se tiene un registro de escorrentía
mostrado en la columna 2.
1 2 3 4 5 6 7 8 9
Orden
del mes
Escorrentía
registrada
Q
Demanda
estimada
D
(
Q
-D
)
 ( Q - D )
Estado
Vol.
embalse
Vol.
Derramado
Volúmenes (mMC/km
2
)
1 137 32 105 105 0 105
2 178 32 146 251 0 Lleno 167 84
3 66 32 34 285 0 Lleno 167 34
4 8 32 -24 261 -24 143
5 8 32 -24 237 -48 174
6 3 32 -29 208 -77 90
7 0 32 -32 176 -109 58
8 3 32 -29 147 -138 29
9 24 32 -8 139 -146 21
10 11 32 -21 118 -167 Máx. 0
11 105 32 73 191 -94 73
12 134 32 102 283 0 Lleno 167 8
13 31 32 -1 292 -1 166
14 80 32 48 340 0 Lleno 167 47
15 48 32 16 356 0 Lleno 167 16
Col. 3: 1050 m3
/dia/km2
x 30,4 dias/mes = 32 mMC/km2
.
Col. 6: Signo negativo indica deficiencia.
Col. 5: Máxima deficiencia = 285 mMC/km2
.
Col. 8: Volumen del embalse suponiendo que está vacío al inicio del periodo: Vi-1 + col. 4
R :  del almacenamiento requerido para garantizar
una demanda constante igual al promedio de los
datos en un periodo de N años.
S : Desviación típica de los datos.
DATOS: Volumen anual de escurrimiento.
A
Pico 1
Pico 2
AM
Pico
siguiente
Tiempo
 (OFERTA - DEMANDA)
+
-
COMPROBACION
mMC = miles de metros cúbicos
El sobrante
precedente al
periodo seco debe
exceder o por lo
menos igualar la
máxima deficiencia
para poder cumplir
con la demanda.
El volumen
acumulado en el
periodo húmedo
después del
periodo seco debe
alcanzar por lo
menos el valor del
inicio, de otra
manera el

6. SIMULACION DE OPERACIÓN DE UN RESERVORIO
Llamado estudio de operación se lleva a cabo para un periodo de tiempo de acuerdo a un
grupo de reglas adoptadas. Puede diseñarse para definir las reglas óptimas para
operación, seleccionar capacidades instaladas o para tomar otras decisiones. Se puede
hacer solamente para un periodo de escurrimiento extremadamente bajo o para el periodo
histórico o registro sintético. En el primer caso se define la capacidad necesaria para
sortear la sequía seleccionada, en tanto que en el último caso el estudio pueda determinar
el agua utilizable o energía para cada año. El estudio más completo indica la probabilidad
de deficiencia de agua o energía.
Ecuación de Continuidad:



























C
I
E
D
P
T
Q
S
E
i
i
S
E 1
Determinación del almacenamiento útil necesario:
Mes
(1)
Q
(MMC)
(2)
E
(mm)
(3)
P
(mm)
(4)
D
(MMC)
(5)
C
(MMC)
(6)
E
(MMC)
(7)
P
(MMC)
(8)
QA
(MMC)
(9)
QA-D
(MMC)
(10)
QA-D
(MMC)
(11)
Ene 2100 3,5 4,5 40 100 203 281 2078 0 0
Feb 4400 5,0 4,7 40 100 291 294 1303 0 0
Mar 30 5,8 0,5 80 30 340 31 -309 -389 -389
Abr 10 6,1 0,7 130 10 356 44 -312 -442 -831
May 5 5,4 0,2 140 5 315 12 -303 -443 -1274
Jun 3 4,6 0 140 3 269 0 -269 -409 -1683
Jul 1 3,0 0 130 1 175 0 -175 -305 -1988
Ago 0 1,7 0 120 0 100 0 -100 -220 -2208
Set 0 0,8 0 80 0 47 0 -47 -127 -2335
Oct 0 1,0 0,4 40 0 59 25 -34 -74 -2409
Nov 0 1,3 0,8 30 0 76 50 -26 -56 -2465
Dic 3 2,4 4,6 30 3 140 288 148 0 -2347
Total 6552 1000 252 2371 1025 4954 2465
Q: Aporte Río D: Demanda Calculada
T: De otras cuencas (riego, saneamiento...)
P: Precipitación C: Compromisos aguas
E: Evaporación del embalse abajo y/oderramado
I : Infiltración del embalse (0) QA: Escurrimiento ajustado
QA = escurrimiento
ajustado.
Ej: Aespejo = 83,33km2
C = 100 MMC ó
vol. mínimo mensual.
E (70%)
P (75%)
(7)=(3) A x 0,7
(8)=(4) A x 0,75
(9)=(2)-(6)-(7)+(8)
(10)=(9)-(5)
(11)=(10)
Máx.deficiencia
V =2465 MMC
D
C
E
I
P
Q
H
H
Presa
A
Río
Presa
T
D C
EST. METEOROLÓGICA
EST. HIDROMETRICA

7. Hi+1
H
En caso que el área del espejo no fuera constante:
i+1 = i + Qi + Ti - Di + Pi - [ Ei + Ci ]
RESTRICCION: mín   i+1   máx
PA EA Regla de operación del sistema
Dependen del nivel
del NAMI del NAMO
VASO RÍO
Curvas de nivel
Presa
NIVEL
H
(msnm)
VOLUMEN
 (MMC)
(FINAL) H i+1
(INICIO) H i
A1 A i+1
 i+1 i
AREA (A)
Km
2
∆i
Ai Ai 1
2
∆H

8. Ejemplo:Funcionamiento del embalse de Clear Creek: 0,0596 ,
ha,
el volumen en m3
.
P
E
Q
C D, dato
0

9. A) Tránsito de avenidas en embalses: (Ref.: Fundamentos de Hidrología de Superficie, Mijares)
Intervalo de tiempo del orden de horas por lo que no se tiene en cuenta la precipitación sobre el embalse, ni
evaporación, ni filtración.
Se tiene la ecuación de continuidad: I-O =ΔS
t
S
S
O
O
I
I i
i
i
i
i
i





 

 1
1
1
2
2
…….
En el caso de un vertedero rectangular sin compuertas, dicha relación está dada por:
0
2
/
3
0
:
)
(
E
E
H
con
E
E
CL
Qv




………
donde:
En el caso de embalses:
T
Q
Q 
v
Q
= Si E>E0
T
Q
=
Q Si E<E0
Método Semigráfico:
















i
i
i
i
i
i
O
t
S
I
I
O
t
S 2
2
1
1
1
1) Trazar la gráfica O vs. O
t
2



- Fijar el t que se usará en el cálculo
- Fijar un valor E > Eo
- Calcular O con las ec. (2) y (3)
- Calcule  de la curva nivel -  del embalse
- Calcule O
t
2



- Repita para otros valores de E.
2) Fijar un nivel inicial (Ei) El NAMO es la condición más crítica
3) Calcular las salidas Oi y di correspondientes a Ei
4) Calcular 




i
i
O
t
2
5) Con las entradas Ii e Ii+1 conocidas de hidrograma de entrada y  en la
ecuación (4), calcular 






1
i
1
i
O
t
2
6) De la curva (I) se determina Oi+1 correspondiente a 
7) Se opera 1
i
1
i
1
i O
t
2
O
2 

 





8) Se pasa al siguiente intervalo haciendo i = i+1 y se vuelve al paso 5) hasta
terminar el hidrograma de entrada.
H
NAME
NAMO
Nivel del
aliviadero
E
E0
E = nivel de la superficie libre en el embalse
E0= nivel de la corona del vertedero
H = carga del vertedero
L= Longitud de la cresta del vertedero
C= Coeficiente de descarga del vertedero, que depende del
sistema de unidades seleccionado y del tipo de vertedero.
QT =Caudal de la obra de toma
3
1
2
I = ingreso
O = salida
S = volumen del reservorio
i , i+1= inicio y fin del intervalo
t = Intervalo de tiempo
)
(
)
( t
O
t
I
dt
dS


4

13. H
i
d
r
o
l
o
g
i
a
A
p
l
i
c
a
d
a
V
e
n
t
e
C
h
o
w