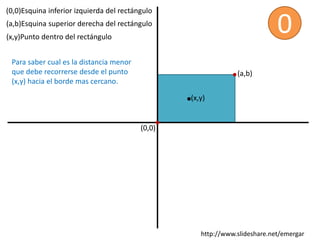
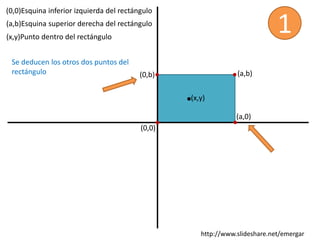
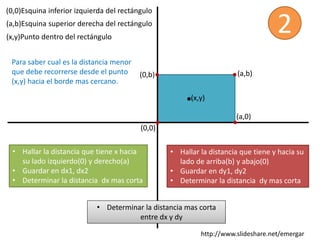
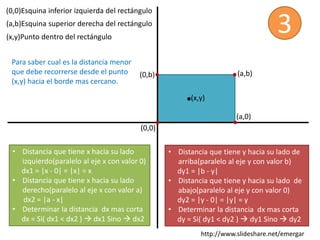
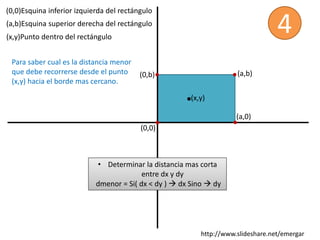
El documento describe cómo calcular la distancia más corta desde un punto (x, y) dentro de un rectángulo hasta uno de sus lados. Se calculan las distancias dx y dy desde el punto hasta los lados paralelos a los ejes x e y, respectivamente, y la distancia más corta es dx si dx < dy, o dy de lo contrario.

1. Menor distancia de un punto
dentro de un rectángulo hacia
algunos de los lados
Emerson Garay
www.youtube.com/emergaray

2. (x,y)
(a,b)
(0,0)
(a,b)Esquina superior derecha del rectángulo
(0,0)Esquina inferior izquierda del rectángulo
(x,y)Punto dentro del rectángulo
Para saber cual es la distancia menor
que debe recorrerse desde el punto
(x,y) hacia el borde mas cercano.
0
http://www.slideshare.net/emergar

3. (x,y)
(a,b)
(0,0)
(a,b)Esquina superior derecha del rectángulo
(0,0)Esquina inferior izquierda del rectángulo
(x,y)Punto dentro del rectángulo
Se deducen los otros dos puntos del
rectángulo
1
(a,0)
(0,b)
http://www.slideshare.net/emergar

4. (x,y)
(a,b)
(0,0)
(a,b)Esquina superior derecha del rectángulo
(0,0)Esquina inferior izquierda del rectángulo
(x,y)Punto dentro del rectángulo
2
(a,0)
(0,b)
• Hallar la distancia que tiene x hacia
su lado izquierdo(0) y derecho(a)
• Guardar en dx1, dx2
• Determinar la distancia dx mas corta
• Hallar la distancia que tiene y hacia su
lado de arriba(b) y abajo(0)
• Guardar en dy1, dy2
• Determinar la distancia dy mas corta
Para saber cual es la distancia menor
que debe recorrerse desde el punto
(x,y) hacia el borde mas cercano.
• Determinar la distancia mas corta
entre dx y dy
• Determinar la distancia mas corta
entre dx y dy
http://www.slideshare.net/emergar

5. (x,y)
(a,b)
(0,0)
(a,b)Esquina superior derecha del rectángulo
(0,0)Esquina inferior izquierda del rectángulo
(x,y)Punto dentro del rectángulo
3
(a,0)
(0,b)
• Distancia que tiene x hacia su lado
izquierdo(paralelo al eje x con valor 0)
dx1 = |x - 0| = |x| = x
• Distancia que tiene x hacia su lado
derecho(paralelo al eje x con valor a)
dx2 = |a - x|
• Determinar la distancia dx mas corta
dx = Si( dx1 < dx2 )  dx1 Sino  dx2
• Distancia que tiene y hacia su lado de
arriba(paralelo al eje y con valor b)
dy1 = |b - y|
• Distancia que tiene y hacia su lado de
abajo(paralelo al eje y con valor 0)
dy2 = |y - 0| = |y| = y
• Determinar la distancia dx mas corta
dy = Si( dy1 < dy2 )  dy1 Sino  dy2
Para saber cual es la distancia menor
que debe recorrerse desde el punto
(x,y) hacia el borde mas cercano.
http://www.slideshare.net/emergar

6. (x,y)
(a,b)
(0,0)
(a,b)Esquina superior derecha del rectángulo
(0,0)Esquina inferior izquierda del rectángulo
(x,y)Punto dentro del rectángulo
4
(a,0)
(0,b)
Para saber cual es la distancia menor
que debe recorrerse desde el punto
(x,y) hacia el borde mas cercano.
• Determinar la distancia mas corta
entre dx y dy
dmenor = Si( dx < dy )  dx Sino  dy
• Determinar la distancia mas corta
entre dx y dy
dmenor = Si( dx < dy )  dx Sino  dy
http://www.slideshare.net/emergar