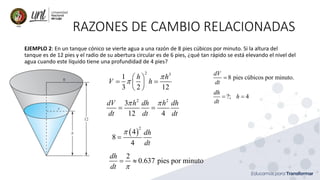
Este documento presenta aplicaciones de cálculo diferencial e integral en ingeniería. Explica conceptos como derivación implícita, derivación de funciones implícitas, máximos y mínimos locales, y razones de cambio relacionadas. Incluye ejemplos sobre derivación implícita, derivación de funciones implícitas, puntos críticos y valores extremos de funciones.

2. CÁLCULO DIFERENCIAL E
INTEGRAL
UNIDAD 3: APLICACIONES EN INGENIERÍA
Marcelo Fernando Valdiviezo Condolo
Primero ‘A’
Carrera de Telecomunicaciones

3. APLICACIONDES DE DERIVADAS

4. DERIVACIÓN IMPLÍCITA
3 3
7
y y x
+ =
En la ecuación no podemos despejar y en términos de x.
y x
 
3
2; 7 8; 1
x y y y
= + = =
La ecuación define a y como una función implícita de x
Sin embargo
No tenemos una función de la forma ( )
y f x
=
y es alguna función desconocida de x. ( )
y x
( ) ( )
3 3
7
y x y x x
+ =
 
 

5. DERIVACIÓN IMPLÍCITA
No tenemos una fórmula para y(x), pero podemos encontrar una relación para x, y(x) y y’(x) mediante la
derivación respecto de x de ambos lados de la ecuación.
( ) ( )
3 3
7
y x y x x
+ =
 
 
( ) ( )
3 3
7
d d d
y y x
dx dx dx
+ =
2 2
3 7 3
dy dy
y x
dx dx
+ =
( )
2 2
3 7 3
dy
y x
dx
+ =
2
2
3
3 7
dy x
dx y
=
+
Derivación
Implícita

6. EJEMPLO 1
Encuentre , si
dy
dx
2 3
4 3 1
x y y x
− = −
Método 1: Podemos despejar explícitamente la y de la ecuación.
( )
2 3
4 3 1
y x x
− = −
3
2
1
4 3
x
y
x
−
=
−
Entonces derivando y respecto a x.
( )( ) ( )( )
( ) ( )
2 2 3 4 2
2 2
2 2
4 3 3 1 8 4 9 8
4 3 4 3
x x x x
dy x x x
dx x x
− − − − +
= =
− −

7. EJEMPLO 1
Encuentre , si
dy
dx
2 3
4 3 1
x y y x
− = −
Método 2: Derivación implícita.
Aplicamos la regla para el producto en el primer término.
( ) ( )
2 3
4 3 1
d d
x y y x
dx dx
− = −
2 2
4 8 3 3
dy dy
x y x x
dx dx
 +  − =
( )
2 2
4 3 3 8
dy
x x xy
dx
− = −
2
2
3 8
4 3
dy x xy
dx x
−
=
−

8. EJEMPLO 1
Encuentre , si
dy
dx
2 3
4 3 1
x y y x
− = −
Método 1:
2
2
3 8
4 3
dy x xy
dx x
−
=
−
( )
4 2
2
2
4 9 8
4 3
dy x x x
dx x
− +
=
−
Método 2:
3
2
2
2
1
3 8
4 3
4 3
x
x x
x
dy
dx x
 
−
−  
−
 
=
−
3
2
1
4 3
x
y
x
−
=
−
( )
4 2 4
2
2
12 9 8 8
4 3
dy x x x x
dx x
− − +
=
−
( )
4 2
2
2
4 9 8
4 3
dy x x x
dx x
− +
=
−
Si una ecuación en x y y determina una función y si esta función es derivable, entonces el
método de la derivación implícita obtendrá una expresión correcta para
( )
y f x
=
dy dx

9. EJEMPLO 2
Encuentre , si
dy
dx
2 3
5 9
x y x
+ = +
( ) ( )
2 3
5 9
d d
x y x
dx dx
+ = +
2
2 15 1
dy
x y
dx
+ =
2
1 2
15
dy x
dx y
−
=

10. EJEMPLO 3
Encuentre la ecuación de la recta tangente a la curva en el punto (0, 1)
( )
3 2
cos 2
y xy xy
− + =
( ) ( )( )
2 2
3 ' 2 ' Sin ' 0
y y x yy y xy xy y
− − − + =
( )
2 2
' 3 2 Sin Sin
y y xy x xy y y xy
− − = +
2
2
Sin
'
3 2 Sin
y y xy
y
y xy x xy
+
=
− −
En el punto (0, 1)
1
'
3
y = ( )
1
1 0
3
1
1
3
y x
y x
− = −
= +
Recta tangente

11. RAZONES DE CAMBIO RELACIONADAS
EJEMPLO 1: Se suelta un pequeño globo en un punto a 150 pies alejado de un observador, quien se encuentra
en el nivel del piso. Si el globo se eleva en línea recta hacia arriba a una velocidad de 8 pies por segundo, ¿qué
tan rápido está aumentando la distancia del observador al globo cuando éste se encuentra a 50 pies de altura?
La distancia desde el observador al punto de lanzamiento permanece sin cambio
conforme t aumenta.
:Número de segundos a partir de que se suelta el globo.
t
:Altura del globo.
h
:Distancia del globo al observador.
s
Dependen de t

12. RAZONES DE CAMBIO RELACIONADAS
EJEMPLO 1: Se suelta un pequeño globo en un punto a 150 pies alejado de un observador, quien se encuentra
en el nivel del piso. Si el globo se eleva en línea recta hacia arriba a una velocidad de 8 pies por segundo, ¿qué
tan rápido está aumentando la distancia del observador al globo cuando éste se encuentra a 50 pies de altura?
8
dh
dt
= ?; 50
ds
h
dt
= =
s y h se encuentran relacionadas por el tiempo (funciones implícitas de t), y también mediante la ecuación
pitagórica
( )
2
2 2
150
s h
= +
2 2
ds dh
s h
dt dt
=
ds dh
s h
dt dt
=
( ) ( )
2 2
50 150 50 10
s = + =
50
h =
ds dh
s h
dt dt
= ( )
50 10 50 8
ds
dt
=
8
2.53
10
ds
pies por segundo
dt
= 

13. RAZONES DE CAMBIO RELACIONADAS
EJEMPLO 2: En un tanque cónico se vierte agua a una razón de 8 pies cúbicos por minuto. Si la altura del
tanque es de 12 pies y el radio de su abertura circular es de 6 pies, ¿qué tan rápido se está elevando el nivel del
agua cuando este líquido tiene una profundidad de 4 pies?
:Profundidad del agua.
h
:Radio de la superficie del agua.
r
8 pies cúbicos por minuto.
dV
dt
=
?; 4
dh
h
dt
= =
2
1
3
V r h

=
Triángulos semejantes
6
12
r
h
=
2
h
r =
2
1
3 2
h
V h

 
=  
 

14. RAZONES DE CAMBIO RELACIONADAS
EJEMPLO 2: En un tanque cónico se vierte agua a una razón de 8 pies cúbicos por minuto. Si la altura del
tanque es de 12 pies y el radio de su abertura circular es de 6 pies, ¿qué tan rápido se está elevando el nivel del
agua cuando este líquido tiene una profundidad de 4 pies?
2 3
1
3 2 12
h h
V h


 
= =
 
 
2 2
3
12 4
dV h dh h dh
dt dt dt
 
= =
8 pies cúbicos por minuto.
dV
dt
=
?; 4
dh
h
dt
= =
2
0.637 pies por minuto
dh
dt 
= 
( )
2
4
8
4
dh
dt

=

15. RAZONES DE CAMBIO
RELACIONADAS

16. DIFERENCIALES

17. MÁXIMOS Y MÍNIMOS

18. MÁXIMOS Y MÍNIMOS
TEOREMA DE EXISTENCIA DE MÁXIMO Y MÍNIMO
En (0, ), no hay máximo ni mínimo.

 
1
En 1,3 , máximo 1, mínimo .
3
= =
( 
1
En 1,3 , no hay máximo, mínimo .
3
=

19. MÁXIMOS Y MÍNIMOS
TEOREMA DE EXISTENCIA DE MÁXIMO Y MÍNIMO
 
En 1,3 , no hay máximo, mínimo 0.
=

20. MÁXIMOS Y MÍNIMOS
 
En , , contiene los puntos fronterizos.
a b
 )
En , , contiene el punto fronterizo izquierdo.
a b
( 
En , , contiene el punto fronterizo derecho.
a b
( )
En , , no contiene ningún punto fronterizo.
a b
( )
' 0
f c = ( )
'
f c =

21. EJEMPLO
Encuentre los puntos críticos de en
( ) 3 2
2 3
f x x x
= − +
1
,2
2
 
−
 
 
Puntos Fronterizos:
1
2
2
y
−
( ) 2
' 6 6 0
f x x x
= − + =
Puntos Estacionarios: para x queda 0 1
y
Puntos Singulares: No existen
Puntos Críticos:
1
, 0, 1 2
2
y
−

22. MÁXIMOS Y MÍNIMOS
TEOREMA DE LOS PUNTOS CRÍTICOS

23. MÁXIMOS Y MÍNIMOS
VALORES EXTREMOS
EJEMPLO: Determine los valores máximo y mínimo de en
3
( )
f x x
=  
2,2
−
2
'( ) 3
f x x
=
'( ) 0 0
f x x
=  =
Puntos Críticos: 2, 0, 2
−
( 2) 8
f − = −
(2) 8
f = Máximo
Mínimo

24. MÁXIMOS Y MÍNIMOS
EJEMPLO: Determine los valores máximo y mínimo de en
3 2
( ) 2 3
f x x x
= − +
1
,2
2
 
−
 
 
2
'( ) 6 6
f x x x
= − +
'( ) 0 0 1
f x x y x
=  = =
1
1
2
f
 
− =
 
 
(0) 0
f =
Máximo
Mínimo
Puntos Críticos:
1
, 0, 1 2
2
y
−
(1) 1
f =
(2) 4
f = −
Máximo

25. TEOREMA DEL VALOR MEDIO
TEOREMA DE ROLLE
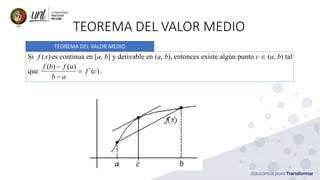
Si f(x) es continua en [a, b] y derivable en (a, b), y si f a = f(b) entonces existe algún punto c ∈ (a, b) tal
que f′
c = 0
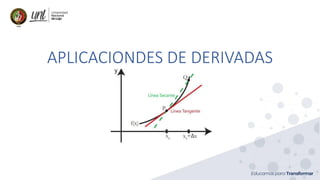
Existe un punto al menos de ese intervalo, en el que la tangente a la curva es horizontal.

26. EJEMPLO

27. TEOREMA DEL VALOR MEDIO
TEOREMA DEL VALOR MEDIO

28. EJEMPLO

29. MONOTONÍA Y CONCAVIDAD
DEFINICIÓN

30. PRIMERA DERIVADA Y MONOTONÍA
TEOREMA DE MONOTONÍA

31. EJEMPLO 1
Si , encuentre en donde f es creciente y en dónde es decreciente
3 2
( ) 2 3 12 7
f x x x x
= − − +
( )( )
2
'( ) 6 6 12 6 1 2
f x x x x x
= − − = + −
Necesitamos conocer en dónde
( )( )
1 2 0
x x
+ − 
y en dónde
( )( )
1 2 0
x x
+ − 

32. EJEMPLO 2
Determine en donde , es creciente y en dónde es decreciente.
2
( )
1
x
g x
x
=
+
( ) ( )
( ) ( )
( )( )
( )
2 2
2 2 2
2 2 2
1 2 1 1
1
'( )
1 1 1
x x x x x
x
g x
x x x
+ − − +
−
= = =
+ + +

33. SEGUNDA DERIVADA Y CONCAVIDAD
DEFINICIÓN

34. SEGUNDA DERIVADA Y CONCAVIDAD
TEOREMA DE CONCAVIDAD

35. EJEMPLO 3
¿En dónde es creciente, decreciente, cóncava hacia arriba y cóncava hacia
abajo
3 2
1
( ) 3 4
3
f x x x x
= − − +
( )( )
2
'( ) 2 3 1 3
f x x x x x
= − − = + −
( )
''( ) 2 2 2 1
f x x x
= − = −

36. EJEMPLO 4
¿En dónde es cóncava hacia arriba y cóncava hacia abajo
2
( )
1
x
g x
x
=
+
( )
2
2
2
1
'( )
1
x
g x
x
−
=
+
( ) ( ) ( )( )( )( )
( )
2
2 2 2
4
2
1 2 1 2 1 2
''( )
1
x x x x x
g x
x
+ − − − +
=
+
( ) ( )( ) ( )( )
( )
2 2 2
4
2
1 1 2 1 4
''( )
1
x x x x x
g x
x
 
+ + − − −
 
=
+
( )
( )
( )
2
3
3 3
2 2
2 3
2 6
''( )
1 1
x x
x x
g x
x x
−
−
= =
+ +

37. EJEMPLO 4
¿En dónde es cóncava hacia arriba y cóncava hacia abajo
2
( )
1
x
g x
x
=
+
( )
2
2
2
1
'( )
1
x
g x
x
−
=
+
( )
( )
2
3
2
2 3
''( )
1
x x
g x
x
−
=
+

38. PROBLEMAS PRÁCTICOS
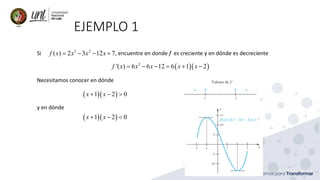
EJERCICIO 1: Encuentre las dimensiones del cilindro circular recto de volumen máximo que puede
inscribirse en un cono circular recto dado.
0
r b V
  
0 0
h a r V
    
El volumen del cilindro inscrito es:
2
V r h

=
Por semejanza de triángulos
a h a
r b
−
=
a
h a r
b
= −
Sustituyendo h en la fórmula para V
2 2 3
a a
V r a r ar r
b b
  
 
= − = −
 
 
Queremos maximizar V para r en [0,b]
2 3
2 3 2
dV a
ar r ar r
dr b b
  
 
= − = −
 
 
Puntos estacionarios
2
0, ,
3
b
b

39. PROBLEMAS PRÁCTICOS
EJERCICIO 1: Encuentre las dimensiones del cilindro circular recto de volumen máximo que puede
inscribirse en un cono circular recto dado.
0
r b V
  
0 0
h a r V
    
El volumen del cilindro inscrito es:
2
V r h

=
Por semejanza de triángulos
a h a
r b
−
=
a
h a r
b
= −
Sustituyendo h en la fórmula para V
2 2 3
a a
V r a r ar r
b b
  
 
= − = −
 
 
Queremos maximizar V para r en [0,b]
2 3
2 3 2
dV a
ar r ar r
dr b b
  
 
= − = −
 
 
Puntos estacionarios:
2
0, ,
3
b
b
Máximo:
2
3
b
3
a
h =

40. PROBLEMAS PRÁCTICOS
EJERCICIO 2: Suponga que un pez nada río arriba con velocidad relativa al agua v y que la corriente del río
tiene velocidad –vc La energía empleada en recorrer una distancia d a contracorriente es directamente
proporcional al tiempo requerido para recorrer la distancia d y el cubo de la velocidad. ¿Qué velocidad v
minimiza la energía empleada en nadar esa distancia.
Velocidad del pez a contracorriente es:
c
v v
−
Tiempo requerido: t
( )
c
d v v t
= −
( )
c
d
t
v v
=
−
Energía requerida para que el pez
recorra la distancia d para un valor
fijo de v
( )
( ) ( )
3
3
c c
d v
E v k v kd
v v v v
= =
− −
Dominio para la función E:
( )
,
c
v 
( )
( ) ( )
( )
2 3
2
3 1
' c
c
v v v v
E v kd
v v
− −
=
−
( )
( )
( )
2
2
' 2 3 0
c
c
kd
E v v v v
v v
= − =
−
Punto crítico en el intervalo
( )
2 3 0
c
v v
− =
3
2
c
v v
=
( )
,
c
v 

41. PREGUNTAS