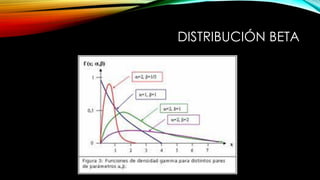
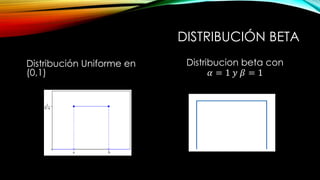
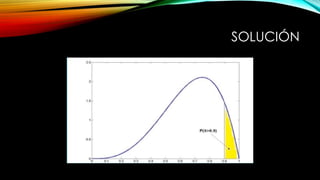
La distribución beta es una familia de distribuciones de probabilidad continua definida en el intervalo (0,1) que depende de dos parámetros. Se utiliza cuando no hay datos históricos sólidos y para variables aleatorias continuas no negativas. Extiende la distribución uniforme y su forma depende de los valores de los parámetros alfa y beta.