Este documento presenta ejemplos sobre el cálculo inverso en la distribución normal estándar y la estandarización de variables aleatorias normales. Explica cómo usar tablas estadísticas para encontrar valores de Z asociados con áreas dadas debajo de la curva normal y cómo convertir una variable aleatoria normal con media y desviación estándar conocidas a una variable estandarizada con media 0 y desviación estándar 1 para facilitar los cálculos.

1. Universidad Los Ángeles de Chimbote CURSO ESTADÍSTICA APLICADA
FACULTAD DE CIENCIAS CONTABLE, FINANCIERAS Y ADMINISTRATIVAS
LECTURA 02: DISTRIBUCIÓN NORMAL (PARTE II)
CALCULO INVERSO EN LA DISTRIBUCIÓN NORMAL ESTÁNDAR.
ESTANDARIZACIÓN.
TEMA 4: CALCULO INVERSO EN LA DISTRIBUCION NORMAL ESTANDAR
En la sesión anterior llevamos acabo el calculo directo en la distribución normal en
donde dada una determinada área teníamos que hallar el valor de la variable
aleatoria normal estándar ahora llevaremos acabo el proceso inverso; es decir dada
una determinada área tenemos que hallar el valor de la variable aleatoria normal
estándar en donde haremos uso de las tablas estadísticas de la distribución normal I
y II y además de las propiedades. A continuación citamos los siguientes ejemplos:
Ejemplo 1:
Si Z n(0,1) , hallar Zo en :
En la Tabla I observamos que el valor de Zo = 2.32, y se obtiene directamente.
Ejemplo 2:
Si Z n(0,1) , hallar Zo en :
95.0]ZZ[P o =≤
____________________________________________ 1
Elaborado por : Mg. Carmen Barreto R.
Fecha : Setiembre 2010
Versión : 2
0.9898
Z00
oP[Z Z ] 0.9898≤ =

2. Universidad Los Ángeles de Chimbote CURSO ESTADÍSTICA APLICADA
FACULTAD DE CIENCIAS CONTABLE, FINANCIERAS Y ADMINISTRATIVAS
En la Tabla I observamos que el valor Zo se encuentra entre 1.64 y 1.65 y llevamos
acabo el proceso de interpolación:
Z Area
1.64 0.9495
Zo 0.95
1.65 0.9505
____________________________________________ 2
Elaborado por : Mg. Carmen Barreto R.
Fecha : Setiembre 2010
Versión : 2
0.95
Z00
0
0
0
0.9505 0.9495 1.65 1.64
0.95 0.9495 Z 1.64
0.001 0.01
0.0005 Z 1.64
Aplicando la regla de tres simples obtenemos :
Z 1.645
− −
=
− −
=
−
=

3. Universidad Los Ángeles de Chimbote CURSO ESTADÍSTICA APLICADA
FACULTAD DE CIENCIAS CONTABLE, FINANCIERAS Y ADMINISTRATIVAS
Ejemplo 3:
Si Z n(0,1) , hallar el valor – Zo en:
01.0]ZZ[P o =≤
En la Tabla I observamos que el valor Zo se encuentra entre -2.33 y -2.32 y llevamos
acabo el proceso de interpolación:
Z Area
-2.33 0.0099
- Zo 0.01
-2.32 0.0102
____________________________________________ 3
Elaborado por : Mg. Carmen Barreto R.
Fecha : Setiembre 2010
Versión : 2
0.01
-Zo 0
0
0
0
0.0099 0.0102 2.33 ( 2.32)
0.01 0.0099 Z ( 2.32)
0.0003 0.01
0.0001 Z 2.32
Aplicando la regla de tres simples obtenenmos :
Z 2.3267
− − − −
=
− − − −
−
=
− +
− = −

4. Universidad Los Ángeles de Chimbote CURSO ESTADÍSTICA APLICADA
FACULTAD DE CIENCIAS CONTABLE, FINANCIERAS Y ADMINISTRATIVAS
Ejemplo 4:
Si Z n(0,1), hallar el valor de Zo en:
10.0]ZZ[P o =≥
Aplicando propiedad:
]ZZ[P1]ZZ[P oo <−=≥
90.0]ZZ[P o =<
En la Tabla I observamos que Zo se encuentra entre 0.8997 y 0.9015 y llevamos
acabo el proceso de interpolación:
Z Area
1.28 0.8997
Zo 0.90
1.29 0.9015
____________________________________________ 4
Elaborado por : Mg. Carmen Barreto R.
Fecha : Setiembre 2010
Versión : 2
0.10
Zo0

5. Universidad Los Ángeles de Chimbote CURSO ESTADÍSTICA APLICADA
FACULTAD DE CIENCIAS CONTABLE, FINANCIERAS Y ADMINISTRATIVAS
Ejemplo 5:
Si Z n(0,1), hallar el valor de -Z0 y Z0 simétricos en:
90.0]ZZZ[P oo =≤≤−
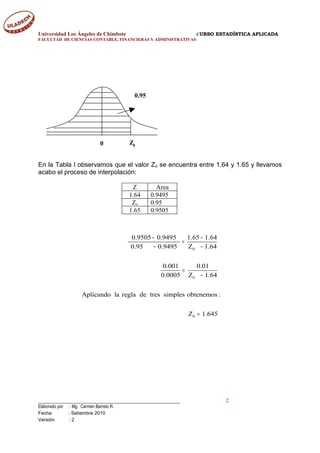
En la Tabla II observamos que Zo se encuentra entre 0.8990 y 0.9011 y llevamos
acabo el proceso de interpolación:
Z Area
1.64 0.8990
Zo 0.90
1.65 0.9011
____________________________________________ 5
Elaborado por : Mg. Carmen Barreto R.
Fecha : Setiembre 2010
Versión : 2
- Zo
Zo0
0.90
0
0
0
0.9015 0.8997 1.29 1.28
0.90 0.8997 Z 1.28
0.0018 0.01
0.0003 Z 1.28
Aplicando la regla de tres simples obtenenmos :
Z 1.282
− −
=
− −
=
−
=

6. Universidad Los Ángeles de Chimbote CURSO ESTADÍSTICA APLICADA
FACULTAD DE CIENCIAS CONTABLE, FINANCIERAS Y ADMINISTRATIVAS
Ejemplo 6:
Si Z n(0,1) , hallar los valores -Zo y Zo simétricos en:
95.0]ZZZ[P oo =≤≤−
En la Tabla II observamos que se encuentra el área dada, por lo tanto no es
necesario interpolar.
Entonces –Zo=-1.96 y Zo= 1.96
____________________________________________ 6
Elaborado por : Mg. Carmen Barreto R.
Fecha : Setiembre 2010
Versión : 2
- Zo
Zo0
0.95
0
0
0
0
0.9011 0.8990 1.65 1.64
0.90 0.8990 Z 1.64
0.0021 0.01
0.001 Z 1.64
Aplicando la regla de tres simples obtenenmos :
Z 1.645
y
Z 1.645
− −
=
− −
=
−
=
− = −

7. Universidad Los Ángeles de Chimbote CURSO ESTADÍSTICA APLICADA
FACULTAD DE CIENCIAS CONTABLE, FINANCIERAS Y ADMINISTRATIVAS
TEMA 5: ESTANDARIZACION DE UNA VARIABLE ALEATORIA NORMAL
Dada una variable aleatoria normal X, con media μ y desvío σ, si definimos otra
variable aleatoria
σ
µ−
=
X
Z entonces la variable aleatoria Z tendrá una distribución
normal estándar.
Al usar la fórmula de transformación cualquier variable aleatoria normal X se
convierte en una variable aleatoria normal estandarizada Z. Mientras los datos
originales para la variable aleatoria X tenían una media y una desviación estándar, la
variable aleatoria estandarizada Z siempre tendrá una media μ = 0 y una
desviación estándar σ = 1.
Veremos algunos ejemplos:
Ejemplo 1:
Si )100,100(nX → , hallar:
a) ]120X[P ≤
9772.0]2Z[P]120X[P
]
10
100120
Z[P]120X[P
=≤=≤
−
≤=≤
____________________________________________ 7
Elaborado por : Mg. Carmen Barreto R.
Fecha : Setiembre 2010
Versión : 2
0.9772
120
100
D.N.G

8. Universidad Los Ángeles de Chimbote CURSO ESTADÍSTICA APLICADA
FACULTAD DE CIENCIAS CONTABLE, FINANCIERAS Y ADMINISTRATIVAS
b) ]130X[P ≥
0013.0]130X[P
9987.01]130X[P
]3Z[P1]130X[P
]
10
100130
Z[P1]130X[P
=≥
−=≥
<−=≥
−
<−=≥
____________________________________________ 8
Elaborado por : Mg. Carmen Barreto R.
Fecha : Setiembre 2010
Versión : 2
0.9772
20
D.N.E.
0.0013
D.N.G.
130100

9. Universidad Los Ángeles de Chimbote CURSO ESTADÍSTICA APLICADA
FACULTAD DE CIENCIAS CONTABLE, FINANCIERAS Y ADMINISTRATIVAS
c) ]75X[P <
062.0]75X[P
]5.2Z[P]75X[P
]
10
10075
Z[P]75X[P
=<
−<=<
−
<=<
____________________________________________ 9
Elaborado por : Mg. Carmen Barreto R.
Fecha : Setiembre 2010
Versión : 2
0.0013
D.N.E.
30
D.N.G.
0.0062
75 100

10. Universidad Los Ángeles de Chimbote CURSO ESTADÍSTICA APLICADA
FACULTAD DE CIENCIAS CONTABLE, FINANCIERAS Y ADMINISTRATIVAS
d) ]125X75[P ≤≤
9878.0]125X75[P
]5.2Z5.2[P]125X75[P
]
10
100130
Z
10
10075
[P]125X75[P
=≤≤
≤≤−=≤≤
−
<
−
=≤≤
NOTA: UTILIZAR LA TABLA II DIRECTAMENTE
____________________________________________ 10
Elaborado por : Mg. Carmen Barreto R.
Fecha : Setiembre 2010
Versión : 2
D.N.E.
0.0062
-2.5 0
D.N.G.
75 125100
0.9878

11. Universidad Los Ángeles de Chimbote CURSO ESTADÍSTICA APLICADA
FACULTAD DE CIENCIAS CONTABLE, FINANCIERAS Y ADMINISTRATIVAS
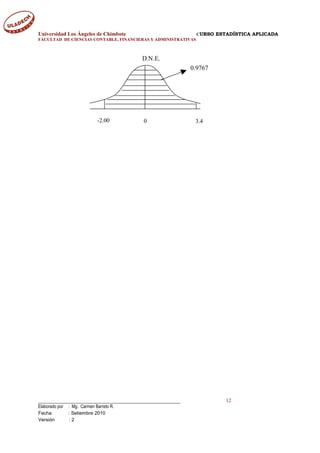
e) ]134X80[P ≤≤
9767.0]125X75[P
0228.09997.0]125X75[P
]00.2Z[P]4.3Z[P]125X75[P
]4.3Z00.2[P]125X75[P
]
10
100134
Z
10
10080
[P]134X80[P
=≤≤
−=≤≤
−<−≤=≤≤
≤≤−=≤≤
−
<
−
=≤≤
____________________________________________ 11
Elaborado por : Mg. Carmen Barreto R.
Fecha : Setiembre 2010
Versión : 2
D.N.E.
- 2.5 2.50
0.9878
D.N.G.
80 134100
0.9767

12. Universidad Los Ángeles de Chimbote CURSO ESTADÍSTICA APLICADA
FACULTAD DE CIENCIAS CONTABLE, FINANCIERAS Y ADMINISTRATIVAS
____________________________________________ 12
Elaborado por : Mg. Carmen Barreto R.
Fecha : Setiembre 2010
Versión : 2
D.N.E.
-2.00 3.40
0.9767