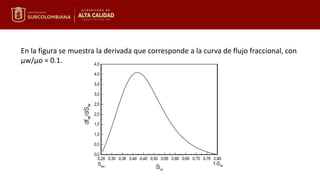
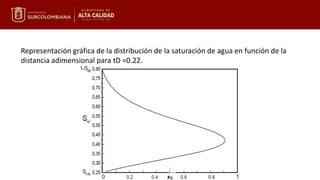
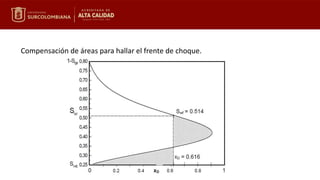
La ecuación de Buckley-Leverett describe el movimiento de un frente de saturación de agua constante a través de un medio poroso. La velocidad del frente de saturación es proporcional a la derivada del flujo fraccional evaluada en esa saturación. Integrando entre el tiempo inicial y final, se puede calcular la posición alcanzada por el frente. Las variables adimensionales de distancia, tiempo y volumen inyectado permiten resolver gráficamente la ecuación para determinar la distribución de la saturación de agua.

1. ECUACIÓN DE BUCKLEY-LEVERETT
Luis Fernando Grajales Moreno
Duván Smith Chala
Ingeniería de Petróleos

2. Se realiza un balance de masa de agua en un elemento de volumen del reservorio
lineal como el de la figura.

3. Donde se obtiene.
Aplicando la definición de derivada y eliminando la densidad del agua por ser el flujo
incompresible. Donde obtenemos.

4. Se busca despejar de la ecuación anterior la velocidad de un frente de saturación de
agua constante:
[dx/dt]Sw . Nótese que la anterior contiene derivadas parciales pues Sw(x,t) y
qw(x,t). Para un frente de saturación de agua constante, d Sw = 0.

5. Además se expresa evaluado a tiempo t como,
Sustituyendo las ecuaciones obtenidas en la ecuación de la lámina número 3,
encontramos:

6. Introduciendo la definición de flujo fraccional, qw = qt .fw.

7. La anterior es la Ec. de Buckley y Leverett: la velocidad de un plano de saturación de
agua constante es proporcional a la derivada del flujo fraccional evaluada a esa
saturación. Integrando entre el tiempo inicial, al comenzar la inyección y un tiempo
cualquiera de recuperación, se puede encontrar el punto alcanzado por el plano de
saturación constante de agua.

8. El valor de la integral es el volumen acumulado de agua inyectada, Wi . Este depende
del tiempo de inyección, siendo la condición inicial usual, Wi = 0 cuando
t = 0. Entonces.

9. Se introducen las siguientes variables adimensionales,,
donde L es la longitud del medio poroso, y
WiD es el número de volúmenes porales de agua inyectados; proporcional al tiempo de
inyección. Por eso, algunos autores (Enhanced Oil Recovery, Lake 1989) lo denominan
tiempo adimensional,

10. Finalmente con estas variables adimensionales obtenemos la siguiente ecuación.
Esta ecuación permite encontrar xD (Sw ) o recíprocamente la distribución de la
saturación de agua S (x) wD . Para ello, hay que calcular la derivada del flujo fraccional
con respecto a la saturación de agua.

11. En la figura se muestra la derivada que corresponde a la curva de flujo fraccional, con
μw/μo = 0.1.

12. Representación gráfica de la distribución de la saturación de agua en función de la
distancia adimensional para tD =0.22.

13. Compensación de áreas para hallar el frente de choque.

14. Distribución de la saturación de agua, mostrando el frente de choque.

15. Entre las variables fundamentales para evaluar un proceso de inyección de agua por
el método de B-L, se debe considerar primero la distribución de la saturación de agua
en el medio poroso, donde se fija un valor al tiempo adimensional.
También se tiene presente el avance del frente de agua en el medio poroso, que
dependerá del volumen de agua inyectado Wi y del tiempo de inyección tD.