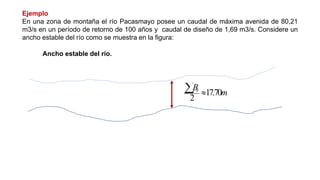
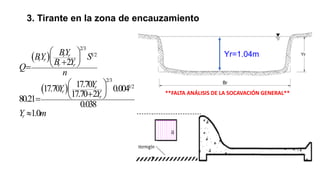
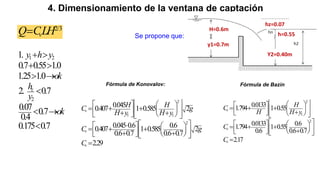
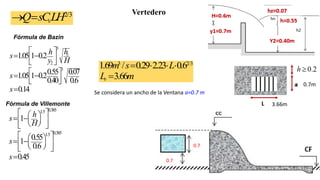
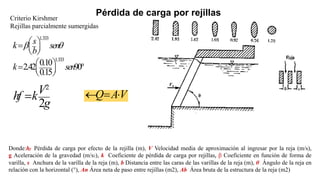
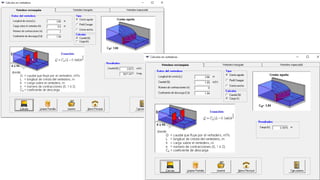
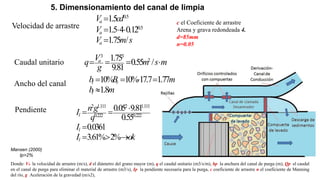
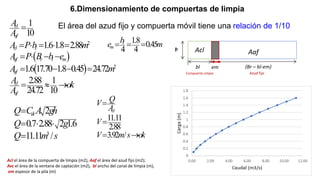
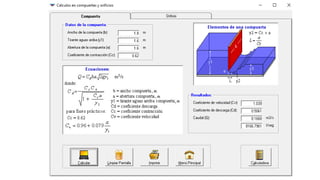
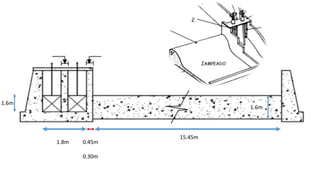
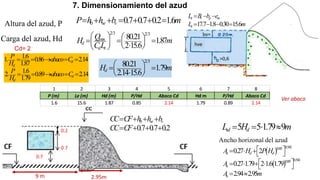
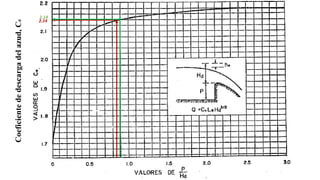
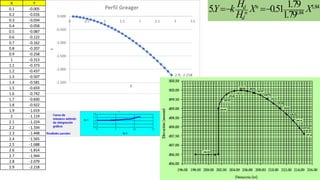
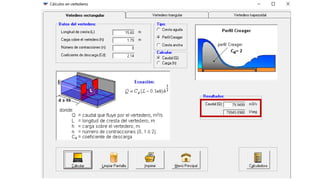
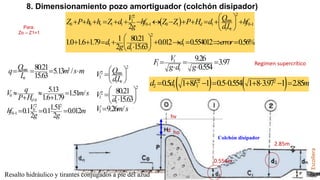
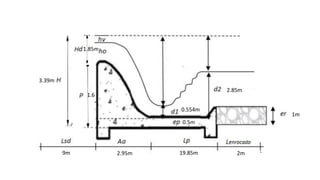
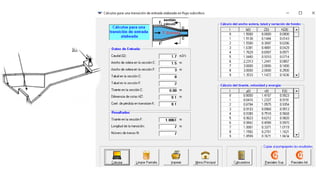
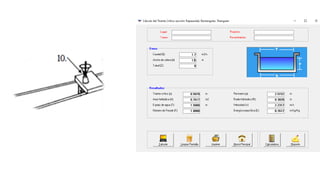
El documento presenta el dimensionamiento de obras hidráulicas como un azud, compuertas de limpieza y canal de purga para el río Pacasmayo. Se calcula el caudal de diseño de 80.21 m3/s y la carga del azud de 1.79 m. Las dimensiones resultantes incluyen un azud de 1.6 m de altura, 15.6 m de longitud efectiva y 2.95 m de ancho.

1. Ejemplo
En una zona de montaña el río Pacasmayo posee un caudal de máxima avenida de 80,21
m3/s en un período de retorno de 100 años y caudal de diseño de 1,69 m3/s. Considere un
ancho estable del río como se muestra en la figura:
Ancho estable del río.
17.70
2
r
B
m



2. 3. Tirante en la zona de encauzamiento
 
 
2/3
1/2
2/3
1/2
2
17.70
17.70 0.004
17.70 2
80.21
0.038
1.0
r r
r r
r r
r
r
r
r
BY
BY S
B Y
Q
n
Y
Y
Y
Y m
 
 

 

 
 

 


Yr=1.04m
**FALTA ANÁLISIS DE LA SOCAVACIÓN GENERAL**

3. 4. Dimensionamiento de la ventana de captación
2/3
v
Q CLH
 H=0.6m
hz=0.07
h=0.55
y1=0.7m
Y2=0.40m
Se propone que:
1 2
2
1.
0.7 0.55 1.0
1.25 1.0
2. 0.7
0.07 0.7
0.4
0.175 0.7
z
y h y
ok
h
y
ok
 
 
 

 

2
1 1
2
0.045
0.407 1 0.585 2
0.045 0.6 0.6
0.407 1 0.585 2
0.6 0.7 0.6 0.7
2.29
v
v
v
H H
C g
H y H y
C g
C
 
   
 
    
 
 
 
   
 
 

   
  
 
 
 
 
   
 
 

Fórmula de Konovalov: Fórmula de Bazin
2
1
2
0.0133
1.794 1 0.55
0.0133 0.6
1.794 1 0.55
0.6 0.6 0.7
2.17
v
v
v
H
C
H H y
C
C
 
 
  
    
  
  
 
 
 
   
  
 
 
  
   
 
 


4. Vertedero
2/3
v
Q sCLH
 
Fórmula de Bazin
Fórmula de Villemonte
3
2
3
1.05 1 0.2
0.55 0.07
1.05 1 0.2
0.40 0.6
0.14
z
h
h
s
y H
s
s
 
 
 
 
 
 
 
 

0.385
1.5
0.385
1.5
1
0.55
1
0.6
0.45
h
s
H
s
s
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 

3 2/3
1.69 / 0.29 2.23 0.6
3.66
v
m s L
L m
   

Se considera un ancho de la Ventana a=0.7 m
0.7
0.7
3.66m
0.7m

5. Dimensionamiento de la reja
ANA (2010) recomienda separación de las varillas (s), 0.025 a 0.10 m material fino
0.10 a 0.20 m material grueso.
L la longitud de la ventana de captación (m), b la distancia entre las caras de las varillas de la reja (m)
s la Anchura de la varilla de la reja (m).
0
0
var 1
N de illas Nespacios
 
 
 
0 0
0 0
( ) ( var )
( ) ( 1 )
15 10
(24.4 ) ( 24.4 1 )
100 100
6.0
total
total
total
total
L N deespacios b N de illas s
L N deespacios b N deespacios s
L
L m
   
    
    

0 3.66 24.4
0.15
L
N deespacios
b
  
Se considera separación entre varillas de 15 cm y diámetros de 10 cm

6. Pérdida de carga por rejillas
Donde:hf Pérdida de carga por efecto de la rejilla (m), V Velocidad media de aproximación al ingresar por la reja (m/s),
g Aceleración de la gravedad (m/s2), k Coeficiente de pérdida de carga por rejillas, β Coeficiente en función de forma de
varilla, s Anchura de la varilla de la reja (m), b Distancia entre las caras de las varillas de la reja (m), θ Ángulo de la reja en
relación con la horizontal (°), An Área neta de paso entre rejillas (m2), Ab Área bruta de la estructura de la reja (m2)
Criterio Kirshmer
Rejillas parcialmente sumergidas
2
2
V
hf k
g

1.333
1.333
0.10
2.42 90º
0.15
s
k sen
b
k sen
 
 
  
 
 
  
 
Q AV
  

8. 5. Dimensionamiento del canal de limpia
Velocidad de arrastre
Donde: Va la velocidad de arrastre (m/s), d el diámetro del grano mayor (m), q el caudal unitario (m3/s/m), bp la anchura del canal de purga (m), Qp el caudal
en el canal de purga para eliminar el material de arrastre (m3/s), Ip la pendiente necesaria para la purga, c coeficiente de arrastre n el coeficiente de Manning
del río, g Aceleración de la gravedad (m/s2),
0.5
0.5
1.5
1.5 4 0.12
1.75 /
a
a
a
V cd
V
V m s

  

c el Coeficiente de arrastre
Arena y grava redondeada 4.
d=85mm
n=0.05
3 3
2
1.75 0.55 /
9.81
a
V
q m s m
g
   
Caudal unitario
Ancho del canal
Pendiente
10% 10%17.7 1.77
1.8
l r
l
b B m
b m
   

2 1.111 2 1.111
0.222 0.222
0.05 9.81
0.55
0.0361
3.61% 2%
l
l
l
n g
I
q
I
I ok

 

  
Mansen (2000)
Ip>2%

9. El área del azud fijo y compuerta móvil tiene una relación de 1/10
 
 
2
2
1
10
1.6 1.8 2.88
1.6 17.70 1.8 0.45 24.72
2.88 1
24.72 10
cl
af
cl l
af r l m
af
cl
af
A
A
A P b m
A P B b e
A m
A ok
A

    
   
   
  
Acl el área de la compuerta de limpia (m2), Aaf el área del azud fijo (m2);
Avc el área de la ventana de captación (m2), bl ancho del canal de limpia (m),
em espesor de la pila (m)
11.11
2.88
3.92 /
cl
Q
V
A
V
V m s ok


 
3
2
0.7 2.88 2 1.6
11.11 /
dc
Q C A gh
Q g
Q m s

  

1.8 0.45
4 4
l
m
b
e m
  
6.Dimensionamiento de compuertas de limpia

11. 0.45m
0.30m
1.8m
15.45m
1.6m
1.6m

12. Altura del azud, P
7. Dimensionamiento del azud
0 0.7 0.7 0.2 1.6
ve v
P h h b m
      
Carga del azud, Hd
2/3 2/3
m
ax 80.21 1.87
2 15.6
d
d e
Q
H m
C L
   
  
   

 
 
Cd= 2
1.6
1. 0.86 2.14
1.87
1.6
2. 0.89 2.14
1.79
d
d
d
d
P abaco C
H
P abaco C
H
    
    
2/3
80.21 1.79
2.14 15.6
d
H m
 
 
 

 
1 2 3 4 5 6 7 8
P (m) Le (m) Hd (m) P/Hd Abaco Cd Hd m P/Hd Abaco Cd
1.6 15.6 1.87 0.85 2.14 1.79 0.89 2.14
0
0.7 0.7 0.2
ve v
CC CF h h b
CC CF
   
   
17.7 1.8 0.30 15.6
e r p m
e
L B b e
L m
  
   
0.7
0.7
0.2
Ver abaco
2.95m
Ancho horizonal del azud
 
 
0.541
0.85
0.541
0.85
0.27 2
0.27 1.79 2 1.6 1.79
2.94 2.95
a d d
a
a
A H P H
A
A m
 
   
 
   
 
 
5 51.79 9
sd d
L H m
   
9 m

13. Coeficiente
de
descarga
del
azud,
C
d 2.14
2.14

14. Perfil de Creager
3
m
ax 80.21
1. 5.13 /
15.6
e
Q
q m s m
L
   
5.13
2. 1.52 /
1.6 1.79
d
q
V m s
P H
  
 
2
3.
2
v
V
h
g

0.12
4. 0.07
1.79
v
d
h Abaco
H
  
Talud vertical
K=0.51 y n=1.84
1.84
1.84
1.79
5. 0.51
1.79
n
d
n
d
H
Y k X X
H
 

15. X Y
0.1 -0.005
0.2 -0.016
0.3 -0.034
0.4 -0.058
0.5 -0.087
0.6 -0.122
0.7 -0.162
0.8 -0.207
0.9 -0.258
1 -0.313
1.1 -0.373
1.2 -0.437
1.3 -0.507
1.4 -0.581
1.5 -0.659
1.6 -0.742
1.7 -0.830
1.8 -0.922
1.9 -1.019
2 -1.119
2.1 -1.224
2.2 -1.334
2.3 -1.448
2.4 -1.565
2.5 -1.688
2.6 -1.814
2.7 -1.944
2.8 -2.079
2.9 -2.218
1.84
1.84
1.79
5. 0.51
1.79
n
d
n
d
H
Y k X X
H
 

16. 1.60m
1.84
1.84
1.79
5. 0.51
1.79
n
d
n
d
H
Y k X X
H
 

18. Colchón disipador
Resalto hidráulico y tirantes conjugados a pie del azud
0
0
2 2
0
0 1
5.13 1.51 /
1.6 1.79
1.51
0.1 0.1 0.012
2 2
d
q
V m s
P H
V
hf m
g g

  
 
  
Para:
Zo – Z1=1
   
2 2
2 1 1
0.5 1 8 1 0.5 0.554 1 8 3.97 1 2.85
d d F m
        
1
1
1
9.26 3.97
0.554
V
F
g d g
  
 
Escollera
 
2
2
m
ax
1
0 0 1 1 0 1 0 1 1 0 1
1
2
1 1
1
2
1 80.21
1.0 1.6 1.79 0.012 0.554012 0.56%
2 15.63
v d
e
Q
V
Z P h h Z d hf Z Z P H d hf
g dL
d d error
g d
 
 
             
 
 
 
        
 

 
hv
ho
2
2 m
ax
1
1
2
2
1
1
1
80.21
15.63
9.26 /
e
Q
V
dL
V
d
V m s
 
 
 
 
 

 

3
m
ax 80.21 5.13 /
15.63
e
Q
q m s m
L
   
8. Dimensionamiento pozo amortiguador (colchón disipador)
Regimen supercrítico
2.85m
0.554m
d

19. Longitud del pozo amortiguador
L Longitud del pozo amortiguador (m), d1 y d2 Tirantes conjugados del resalto hidráulico (m), H Carga del agua para máximas
avenidas (m), F1 Número de Froude en la sección 1. ep el espesor del pozo amortiguador (m), q Caudal unitario que pasa por
el azud (m3/s/m); z Diferencia de niveles aguas arriba y aguas abajo del azud (m), Krochin (1978) mínimo 0,3 m.
    
2 1
5 6 5.5 2.85 0.554 12.62
p
L a d d m
    
1 1
6 6 0.554 3.97 19.81
p
L dF m
    
   
2 1
5 5 2.85 0.554 11.47
p
L d d m
    
2
4 4 2.85 11.39
p
L d m
   
   
2 1
2.5 1.4 2.5 1.4 2.85 0.554 8.58
p
L d d m
     
Espesor del pozo amortiguador
Traimovich
Schoklitsch
Safranez
USBR
Baklmnetev
-Martzke
Pavloski
3
m
ax 80.21 4.05 /
19.81
p
Q
q m s m
L
   
   
0.25 0.25
2
0.2 0.2 4.05 3.39 2.85 0.5
p
e q H d m
    
Considero el máximo valor: 19.81 m (valorar aspectos económicos)

20. Espesor del enrocado
0.25 0.25
0.5 3.39
0.6 0.6 4.05 1.04 1
r
H
e q m m
g g
   
    
   
   
er Espesor del enrocado (m), H Carga del agua para máximas avenidas (m), q
caudal unitario en el disipador (m3/s/m), Lenroca Longitud del enrocado (m), L
Longitud del pozo amortiguador (m),, Cb el coeficiente de Bligh según tipo de
suelo. Tirantes conjugados del resalto hidráulico (m), F1 Número de Froude en
la sección 1. e el espesor del pozo amortiguador (m), q Caudal unitario
(m3/s/m); z Diferencia de niveles aguas arriba y aguas abajo del azud (m),
Krochin (1978) mínimo 0,3 m.
0,624 0,624 9 4.05 3.39 19.1 1.32
enroca b p
L C qH L m
       
Longitud del enrocado
Lecho Grano Coef Bligh (Cb)
Arena Fina 0.005-0.01 18
Limo 0.1-0.25 15
Arena fina 0.2-1 12
Arena Gruesa 9
Gravas Arenas 9
Bolnones y Arena 4 a 6
Arcilla 6 a 7
   
2 1
9 9 2.85 0.554 19.81 0.84
enroca p
L d d L m
      
Pardo y Alegret (2012)
Longitud de enrocado se recomienda 2 m

21. 2m
19.85m
2.95m
9m
1m
0.5m
2.85m
0.554m
1.85m
3.39m
1.6