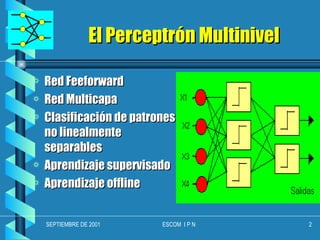
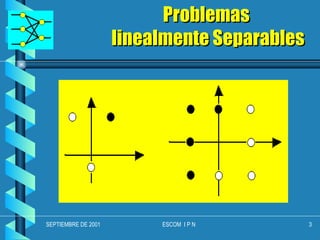
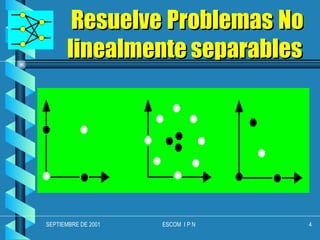
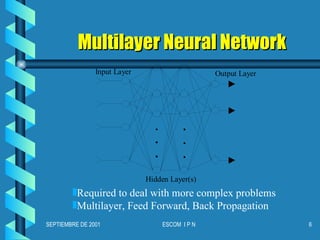
El documento describe el perceptrón multicapa, una red neuronal que puede resolver problemas de clasificación no linealmente separables. Explica que un perceptrón de 3 capas puede formar cualquier región convexa en el espacio de entrada, mientras que un perceptrón de 4 capas puede generar regiones de decisión arbitrariamente complejas partiéndolas en pequeños hipercubos. Finalmente, indica que en teoría un perceptrón de 4 capas puede resolver una gran variedad de problemas de clasificación siempre que las entradas sean analógicas y la salida digital.