Descargar para leer sin conexión
Subido porJhoan Tenjo
Enfoques
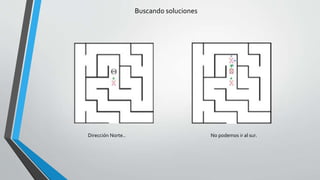
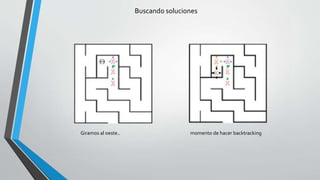
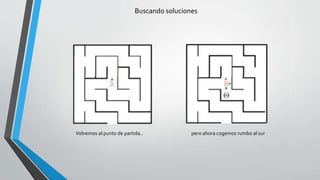
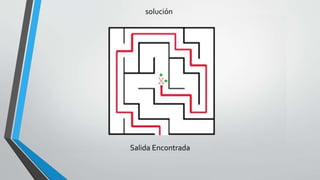
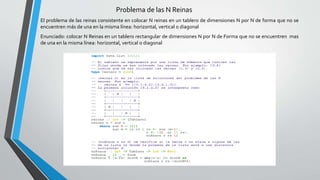
Este documento describe dos enfoques de programación recursiva: recursividad por cola (tail recursion) y backtracking. La recursividad por cola elimina las llamadas recursivas repetitivas para mejorar el rendimiento, mientras que el backtracking genera todas las posibles combinaciones para encontrar una solución, retrocediendo cuando una opción no funciona. También presenta ejemplos como el factorial y resolver un laberinto usando estos enfoques.
Enfoques
- 1. INSTITUTO UNIVERSITARIO POLITECNICO “SANTIAGOMARIÑO” CATEDRA: Programación No Numérica II Enfoques Realizado por: TenjoV. Jhoan M C.I: 20326602 Porlamar, Julio del 2014
- 2. (Tail Recursion) oMétodo de ir hacia adelante La recursividad es una técnica de programación que consiste en que una serie de instrucciones se repiten como una sub tarea de la tarea principal, es decir, las funciones, procesos o rutinas se llaman a sí mismos cada vez que lo requieran y se ejecutan repetidas veces hasta que se satisface una condición específica. Sin embargo, la recursividad en algunos casos, tiene un costo computacional alto, debido a las constantes llamadas a la misma función, rutina y muchas veces estas llamadas consumen demasiada memoria. En algunos algoritmos recursivos, se puede implementar un caso de recursividad especial llamado Tail recursión (recursividad por cola), la cual es una técnica para optimizar la recursividad eliminando las constantes llamadas recursivas. Tail recursion es cuando la llamada recursiva es la última instrucción de la función. Sin embargo, las funciones tail recursive deben cumplir la condición que en la parte que realiza la llamada a la función, no debe existir ninguna otra sentencia. Una ventaja de la recursividad por cola es que podemos evitar la sobrecarga de cada llamada a la función y nos evitamos el gasto de memoria de pila. Con una función tail recursive se puede evitar lo que se conoce como stack overflow, que ocurre cuando la pila de llamadas (call stack) consume mucha memoria.
- 3. Veamos esta técnicacon un ejemplo muy conocido que es encontrar el factorial de un número. Esta simple función obtiene el factorial de un número de la manera recursiva convencional: La explicación es sencilla, llamamos a la misma función fact hasta que n sea igual a 1, en ese momento la recursividad se detiene. Esta simple función obtiene el factorial de un número de la manera recursiva convencional: La explicación es sencilla, llamamos a la misma función fact hasta que n sea igual a 1, en ese momento la recursividad se detiene. Digamos que ingresé 15, si compilamos el programa la función me daría 2004310016, lo cual es correcto, pero hay que tener en cuenta todas las llamadas recursivas que hizo la función fact_recursivo, es decir, la función tiene que calcular el factorial de 14 y este el fact de 13, y este el fact de 12… sucesivamente hasta 1. Tenemos un crecimiento del número de llamadas recursivas. Ahora vamos a realizar la misma función usando tail recursion. En este caso no se necesita guardar un marco de pila para cada llamada recursiva, y el algoritmo se comporta como si fuera iterativo. 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 int fact_recursivo(int n) { if(n == 1) return n; else return n * fact_recursivo(n-1); } int main() { int num = 0; cout << "Ingresa un nro " << endl; cin >> num; cout << "Su factorial es " << fact_recursivo(num); return 0; }
- 4. (Backtracking) o Métodode ir hacia atrás Backtracking o método de ir hacia atrás se asemeja a un recorrido en profundidad dentro de un grafo dirigido. La técnica crea todas las posibles combinaciones de elementos para obtener una solución. Su principal virtud es que en la mayoría de las implementaciones se puede evitar combinaciones, estableciendo funciones de acotación reduciendo el tiempo de ejecución. El backtracking esta muy relacionado con la búsqueda combinatoria. La idea es encontrar la mejor combinación posible, por esto se puede decir que es una búsqueda en profundidad, durante la búsqueda: Si se encuentra con una alternativa incorrecta la búsqueda retrocede al punto anterior y toma la siguiente alternativa. Cuando se terminan las posibilidades, se vuelve a la elección anterior y se toma la siguiente opción
- 5. ejemplo tomar es elde encontrar la salida en un laberinto. ¿Por qué podemos tomarlo como ejemplo? Por que un laberinto puede comportarse como un grafo, donde cada cruce puede ser un nodo donde debemos tomar una decisión que conducen a otros nodos. o Si la posición actual está fuera del laberinto, devolverTRUE para indicar que hemos encontrado una solución. o Si la posición actual está marcada, devolver FALSE para indicar que ya habíamos estado aquí. o Marcar la posición actual. Para cada una de las 4 direcciones posibles (N,S,E,O){ Si (en la dirección elegida no chocamos contra un muro) { Moverse un paso en la dirección indicada Intentar resolver el laberinto desde ahí recursivamente. Si la llamada recursiva nos permite salir del laberinto, devolverTRUE } } Quitar la marca de la posición actual. Devolver FALSE para indicar que ninguna de las 4 direcciones nos permitió llegar a una solución desde la posición actual
- 6. Dirección Norte.. Nopodemos ir al sur. Buscando soluciones
- 7. Giramos al oeste..momento de hacer backtracking Buscando soluciones
- 8. Volvemos al puntode partida.. pero ahora cogemos rumbo al sur Buscando soluciones
- 9.
- 10. Problema de lasN Reinas El problema de las reinas consistente en colocar N reinas en un tablero de dimensiones N por N de forma que no se encuentren más de una en la misma línea: horizontal, vertical o diagonal Enunciado: colocar N Reinas en un tablero rectangular de dimensiones N por N de Forma que no se encuentren mas de una en la misma línea: horizontal, vertical o diagonal
- 11. Conclusión El manejo dealgoritmos tomando en cuenta el método de ir hacia adelante aporta cierto interés con el termillo llamado recursivo, mas que todo se especializa en eliminar capas de una maneras por decirlo así ya que con el hecho de eliminar e implementar una nueva estructura de algoritmo se cumple la condición que se requiere.Y es que por esa razón se determina un valor a la solución. Sin embargo el método de ir hacia atrás conocí y estudie el ejemplo tomado. dice: recorrer y encontrar soluciones. Esta también puede llamarse una toma de decisiones porque cada vez que se elige una acción a realizar se juzga el paso que se da y no se garantiza una solución en ese momento, es por ello que consta de pasos indeterminados para llegar a la solución. Para llegar al punto del problema de las N Reinas determine que puede tomarse como un juego el especifico y que puede ser practico a la vez, como también tiene cierto parecido al sudoku. Como se representa como un algoritmo tiende a ser mas exacto y tiende hacer mas exacto con su representación de códigos.
- 12.