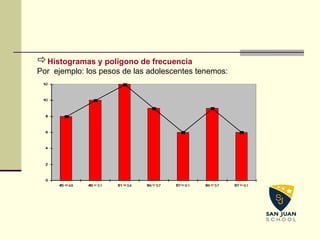
La estadística es una rama de las matemáticas que se encarga de recopilar, organizar y analizar datos para entender fenómenos en diversas ciencias. Utiliza conceptos como población, muestra, y variables (cuantitativas y cualitativas) para realizar análisis confiables a partir de encuestas y estudios. Los gráficos estadísticos, como diagramas de barras y histogramas, ayudan a visualizar la información de manera clara y rápida.

1. ESTADÍSTICA

2. ¿Qué estudia la Estadística?
 La Estadística es la rama de la Matemática
que se ocupa de recopilar datos (en censos,
encuestas, etc), de organizarlos para una
mejor comprensión del fenómeno que se
desea estudiar y de analizarlos con un
determinado objetivo.
 La estadística se aplica a todas las ciencias,
pues facilita el estudio de hechos del mundo
o de la sociedad.

3. Ejemplo:
Se hizo una encuesta a 8976 personas, de las cuales 8707 respondieron que
calman su dolor de cabeza tomando una aspirina. Si la encuesta está bien
hecha, este dato puede ser utilizado por los médicos, quienes podrían afirmar
que si un paciente sufre de dolor de cabeza, tiene un 97 % de probabilidad de
calmarla tomando una aspirina.

4. Algunos conceptos de Estadística
Datos que se recopilan Población
Se registra el peso de los alumnos de un curso Alumnos del curso
Se hace una encuesta en las viviendas de un barrio para determinar cuántas
personas viven en cada una de ellas
Habitantes del barrio
Población: Llamamos población al conjunto de individuos (personas,
animales, cosas) sobre la cuál se estudia una determinada característica.
Ejemplos:
El tamaño de la población es el número de individuos que la componen.

5. Cuando el tamaño de una población es muy grande, se trabaja con una
parte de ella llamada muestra.
Ejemplo: A una consultora le encargan hacer un estudio acerca de cuál es la
intención del voto de los ciudadanos de una ciudad en las próximas
elecciones. Como no es posible encuestar a todos los ciudadanos, la
consultora toma un grupo de 500 y sobre él analiza la variable. Con los datos
recopilados sobre esta muestra, se puede hacer una proyección de los votos
que obtendrá cada candidato.
Importante!!! Para que el estudio estadístico sea confiable, es muy
importante que la selección de los individuos de una muestra resulte
representativa de la población que se analiza, o sea, se deben obtener de
ella resultados aproximadamente iguales a los que se hubieran obtenido
considerando el total de la población.

6. VARIABLES ESTADÍSTICAS
CUANTITATIVAS
Son medibles y se expresan
por medio de un número
CUALITATIVAS
· No se pueden medir y se
expresan con palabras.
· Tiene distintas
modalidades, que son las
diferentes situaciones
que se pueden presentar.
Ejemplos:
Sexo: Femenino – Masculino
Color de ojos
Color del cabello
DISCRETAS
Cuando solo pueden
tomar algunos valores
determinados.
Ejemplos:
Nº de padres vivos
Nº de hermanos
CONTINUAS
Cuando pueden tomar
infinitos valores
comprendidos entre dos
valores determinados.
Ejemplos:
Altura, peso, etc
Variables: son los caracteres o cualidades de la población que es objeto
de estudio o análisis. Pueden ser:

7. Frecuencia absoluta: es el número de veces que se repite una observación o
valor de la variable (f).
Frecuencia relativa de una observación: es el cociente entre su frecuencia
absoluta y el número total de observaciones realizadas (fr
).
n
f
r
f 

8. • La tabla que muestra la frecuencia relativa, absoluta y acumulada se
llama distribución de frecuencias.
• La suma de las frecuencias absolutas es el total de observaciones.
• La suma de las frecuencias relativas es siempre 1.
• Si multiplicamos por 100 cada frecuencia relativa, obtenemos el
porcentaje de cada valor de la variable (%).
Porcentaje = frecuencia relativa . 100
100
.
% r
f

Observaciones

9. Notas f fr
%
1 2
2 4
3 3
4 5
5 6
6 8
7 5
8 3
9 2
10 2
Total 40
Ejemplo 1:
A los alumnos de 1° A se les tomó una evaluación
escrita. En la tabla se detallan las notas que
obtuvieron.
Esta tabla recibe el nombre de distribución de
frecuencias
¿Cuántos alumnos hay en el curso?
¿Cuántos aprobaron?
¿Cuántos resultaron aplazados?

10. Datos Agrupados en Intervalos
Cuando trabajamos con una variable
continua, podemos agrupar los
valores en intervalos. Para eso es
necesario conocer el rango de la
variable (diferencia entre el mayor y
el menor valor que toma la variable)
y luego dividirlo en partes iguales
llamadas intervalos. En los
intervalos se incluye el primer valor,
pero no el último, salvo en el último
intervalo en el que se incluyen los
dos.

11. Gráficos Estadísticos
Los gráficos estadísticos se utilizan muchísimo, y con
ellos la información obtenida puede ser leída con
claridad y rapidez. Los gráficos más usados son:
diagramas de barras, gráficos circulares,
pictogramas, histogramas, polígono de
frecuencia.
Para variables discretas: Para variables continuas:
- diagramas de barras - histogramas
- pictogramas - polígono de frecuencia
- gráfico de torta - gráfico de torta

12. Histogramas y polígono de frecuencia
Por ejemplo: los pesos de las adolescentes tenemos:
0
2
4
6
8
10
12
45 - 48 48 - 51 51 - 54 54 - 57 57 - 61 54 - 57 57 - 61
0
2
4
6
8
10
12
45 - 48 48 - 51 51 - 54 54 - 57 57 - 61 54 - 57 57 - 61