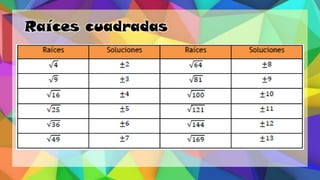
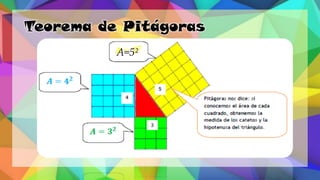
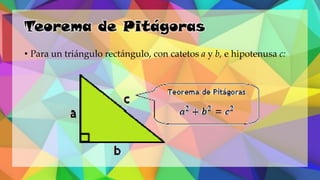
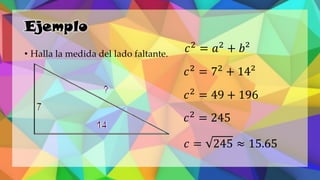
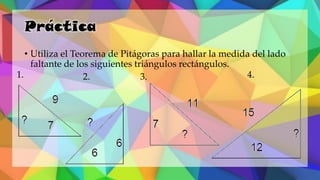
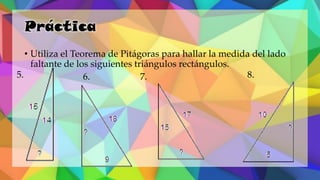
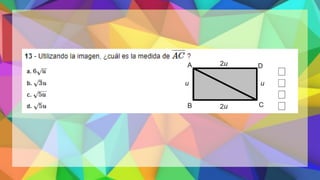
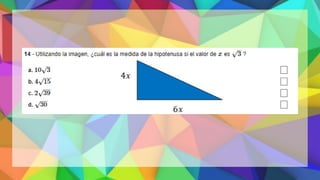
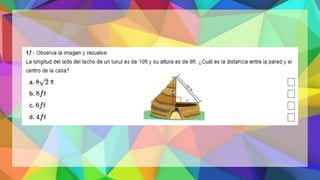
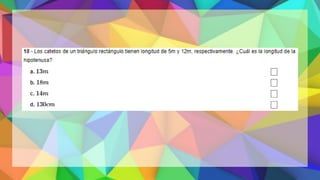
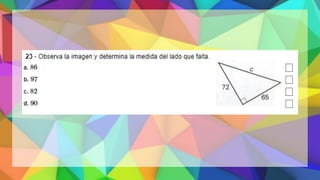
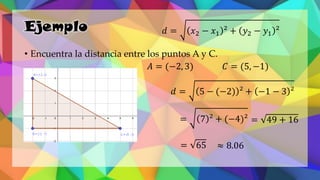
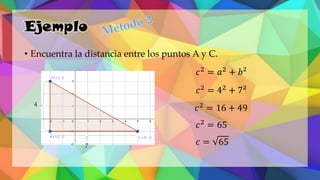
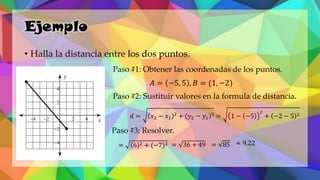
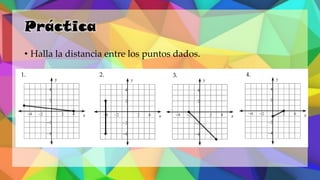
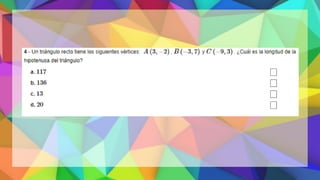
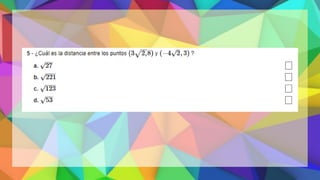
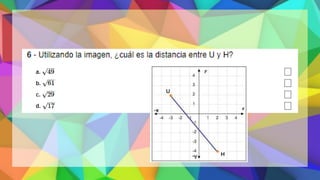
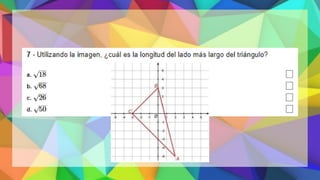
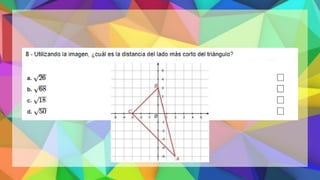
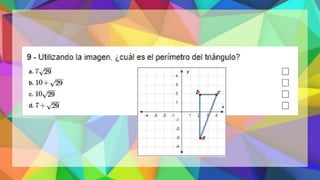
Este documento proporciona una explicación del Teorema de Pitágoras. Explica que Pitágoras fue un matemático griego que descubrió que en un triángulo rectángulo, la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa. A continuación, proporciona ejemplos para demostrar cómo aplicar este teorema para calcular el lado desconocido de un triángulo rectángulo. Finalmente, incluye ejercicios de práctica para que los estudiantes apliqu

1. Teorema de
Pitágoras
Repaso META PR
U8.4: Pitágoras y el triángulo recto
Prof. Rosa E. Padilla Torres

2. Raíces cuadradas
• Las raíces cuadradas son números que se obtienen de forma
perfecta o por medio tecnológico, como una calculadora.
• En las raíces cuadradas perfectas, se obtienen números enteros
del cuadrado de un número.
• Forma general:
2
𝑛 = 𝑛

3. Raíces cuadradas
• Definición:
𝑎 = b ⟺ 𝑏2
= 𝑎

4. Raíces cuadradas

5. Teorema de Pitágoras
• Pitágoras fue un matemático griego que
realizó muchas aportaciones científicas.
• Entre sus aportaciones más importantes, se
encuentra el Teorema de Pitágoras.

6. Triángulo – Triángulo rectángulo
• Triángulo es un polígono de tres lados.
• Un triángulo rectángulo es el triángulo que tiene uno sus
ángulos que mide 90°.
• La hipotenusa es el lado más largo.
• Siempre está al lado opuesto del
ángulo recto. Cateto
Cateto
hipotenusa

7. Teorema de Pitágoras
A=5²

8. Teorema de Pitágoras
• Para un triángulo rectángulo, con catetos a y b, e hipotenusa c:

9. Ejemplo
• Halla la medida del lado faltante.
𝑐2
= 𝑎2
+ 𝑏²
𝑐2
= 72
+ 14²
𝑐2
= 49 + 196
𝑐2
= 245
𝑐 = 245 ≈ 15.65

10. Ejemplo
• Halla la medida del lado faltante.
𝑐2
= 𝑎2
+ 𝑏²
262
= 132
+ 𝑏²
676 = 169 + 𝑏²
676 − 169 = 𝑏²
𝑏2
= 507
𝑏 = 507 ≈ 22.52

11. Práctica
• Utiliza el Teorema de Pitágoras para hallar la medida del lado
faltante de los siguientes triángulos rectángulos.
1. 2. 3. 4.

12. Práctica
• Utiliza el Teorema de Pitágoras para hallar la medida del lado
faltante de los siguientes triángulos rectángulos.
5. 6. 7. 8.

13. Práctica META PR

39. Triángulos en el plano
cartesiano
• Distancia entre dos puntos en el plano
• Dos puntos en el plano, con coordenadas 𝑥1, 𝑦1 y 𝑥2, 𝑦2 , la distancia
entre los dos puntos está dada por:
𝑥2 − 𝑥1 ² + 𝑦2 − 𝑦1 ²

40. Ejemplo
• Encuentra la distancia entre los puntos A y C.
𝑑 = 𝑥2 − 𝑥1 ² + 𝑦2 − 𝑦1 ²
𝐴 = (−2, 3) 𝐶 = (5, −1)
= 7 ² + (−4)²
𝑑 = 5 − (−2) ² + −1 − 3 ²
= 49 + 16
= 65 ≈ 8.06

41. Ejemplo
• Encuentra la distancia entre los puntos A y C.
4
7
𝑐2
= 𝑎2
+ 𝑏²
𝑐2
= 42
+ 7²
𝑐2
= 16 + 49
𝑐2 = 65
𝑐 = 65

42. Ejemplo
• Halla la distancia entre los dos puntos.
Paso #1: Obtener las coordenadas de los puntos.
𝐴 = −5, 5 , 𝐵 = (1, −2)
Paso #2: Sustituir valores en la formula de distancia.
𝑑 = 𝑥2 − 𝑥1 ² + 𝑦2 − 𝑦1 ² = 1 − −5
2
+ −2 − 5 2
Paso #3: Resolver.
= 6 2 + (−7)2 = 36 + 49 = 85 ≈ 9.22

43. Práctica
• Halla la distancia entre los puntos dados.
1. 2. 3. 4.

44. Ejemplo
• Halla la distancia entre dos puntos, dadas sus coordenadas.
0, −2 , (−5, −1)
Paso #1: Identificar las coordenadas.
0, −2 , (−5, −1)
𝑥1, 𝑦1 𝑥2, 𝑦2
Paso #2: Sustituir valores en la formula de distancia.
𝑑 = 𝑥2 − 𝑥1 ² + 𝑦2 − 𝑦1 ² = −5 − 0 2 + −1 − (−2) 2
Paso #3: Resolver.
= −5 2 + 1² = 25 + 1 = 26

45. Práctica
• Dadas las coordenadas de dos puntos, halla la distancia entre
ellos.
1. 3, 8 , (9, 10) 2. 10, 1 , (9, −4)
3. −8, 10 , (−6,7) 4. 6, 4 , (−5, −1)

46. Repaso Pruebas META
PR

56. Referencia
• La Nueva Escuela Virtual
• Planificaciónturbo.com