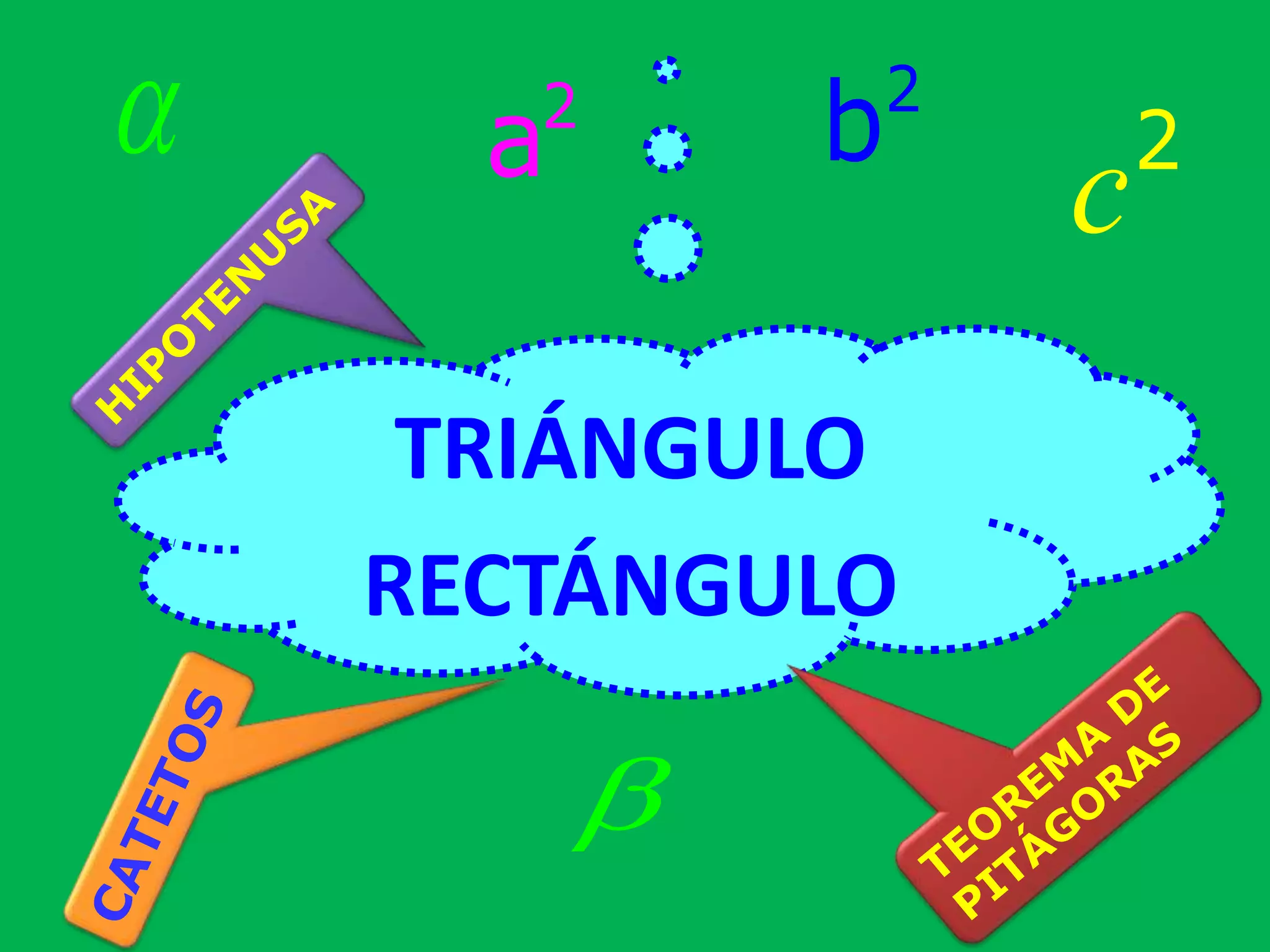
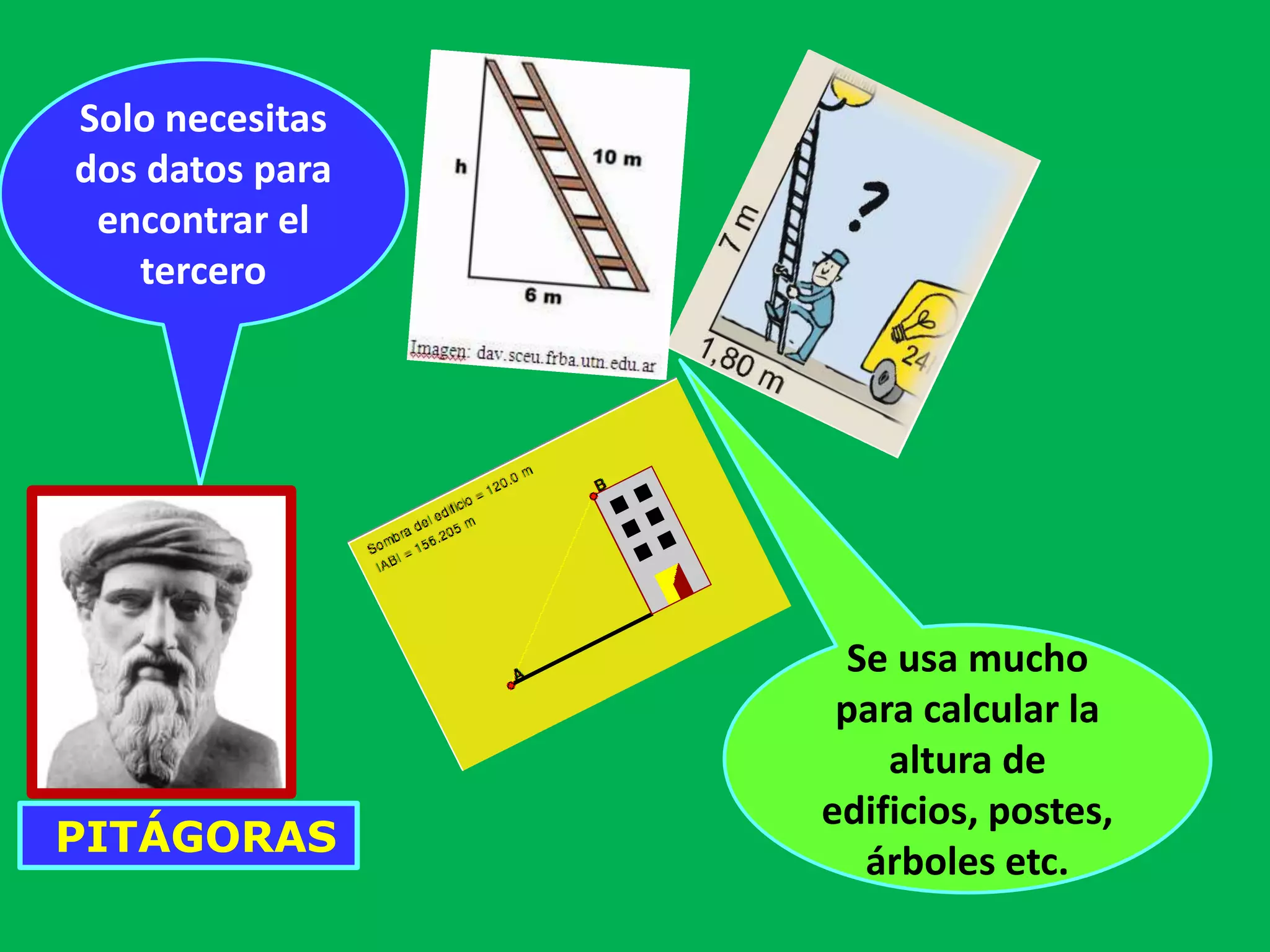
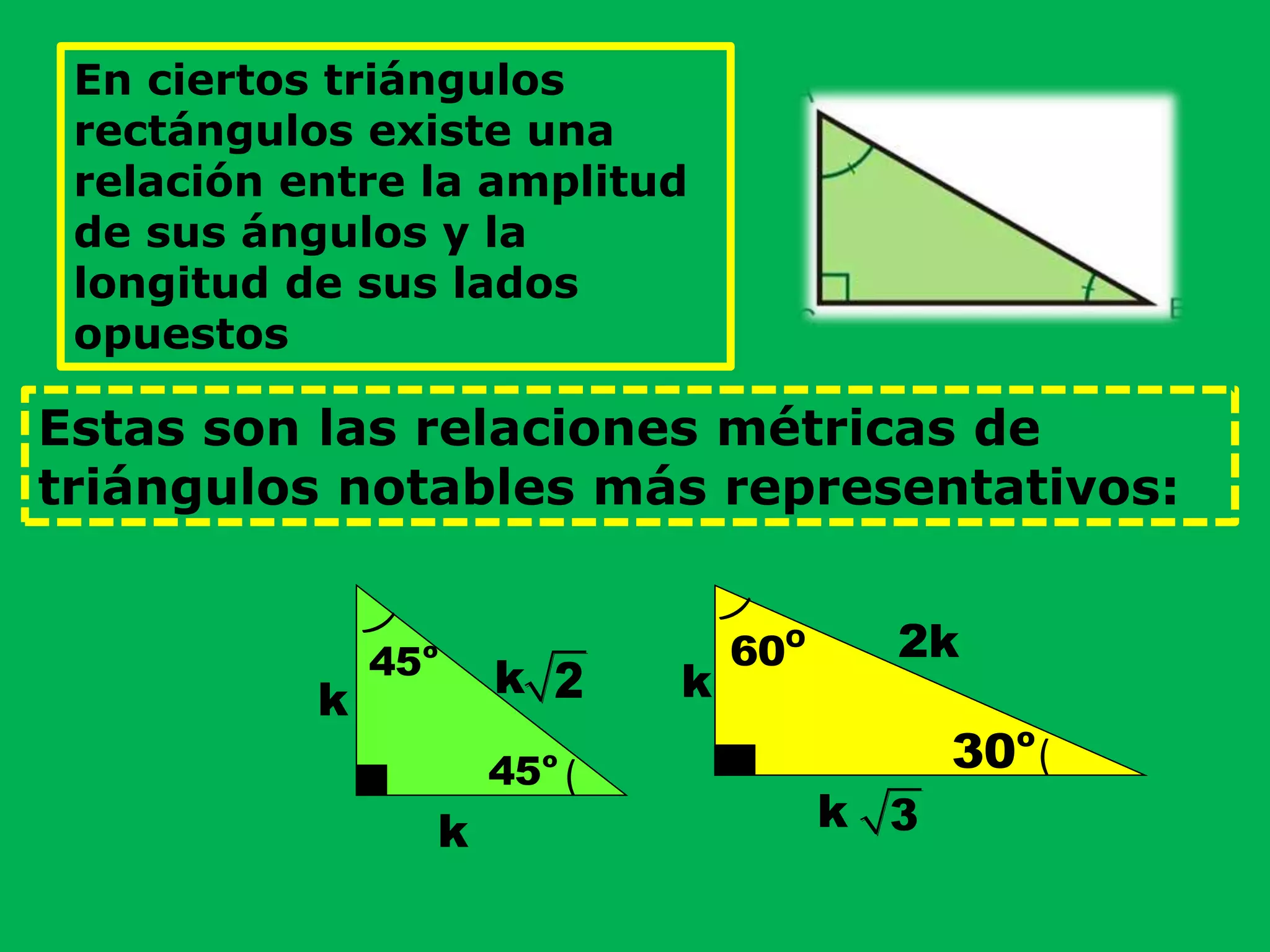
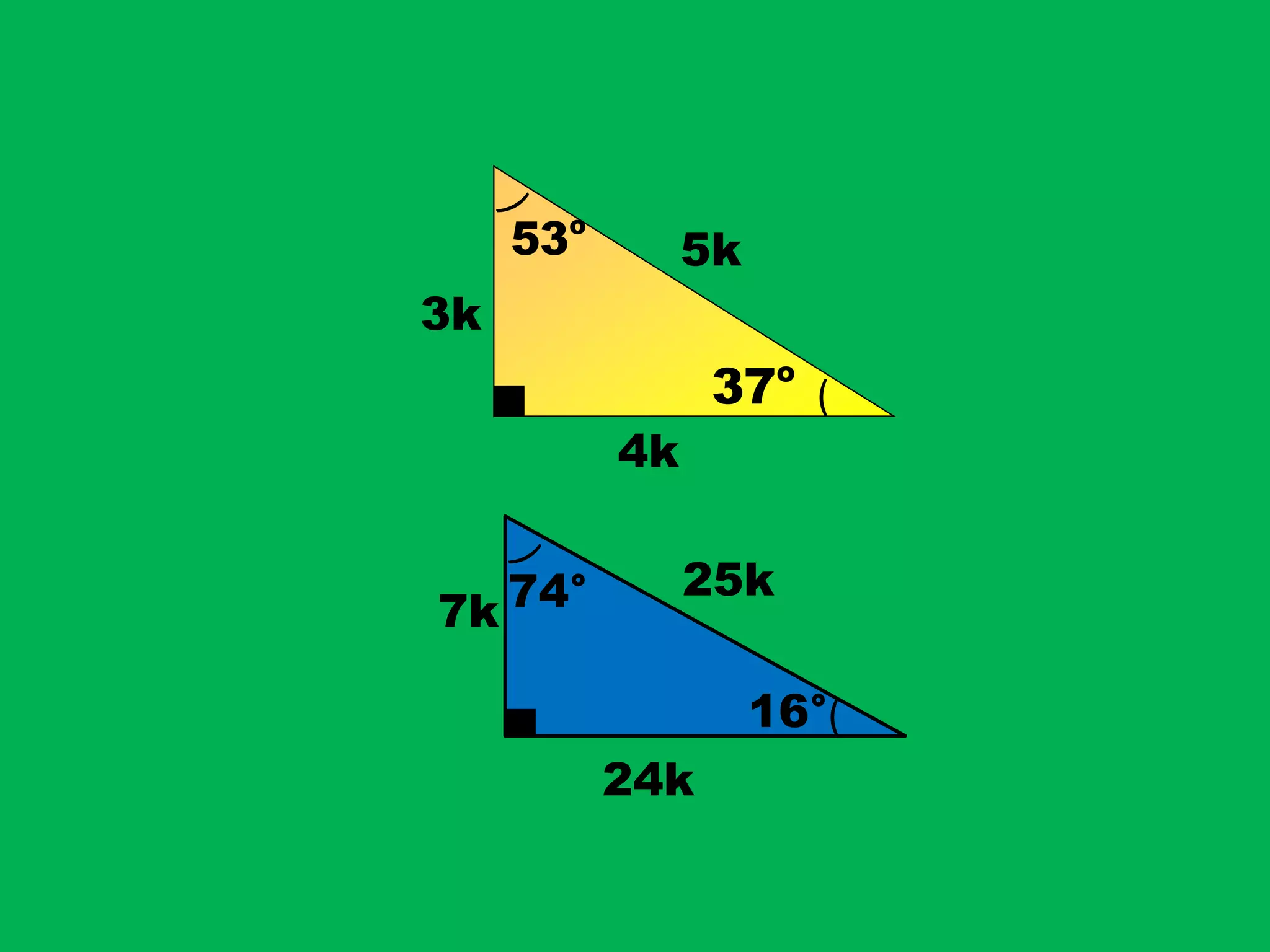
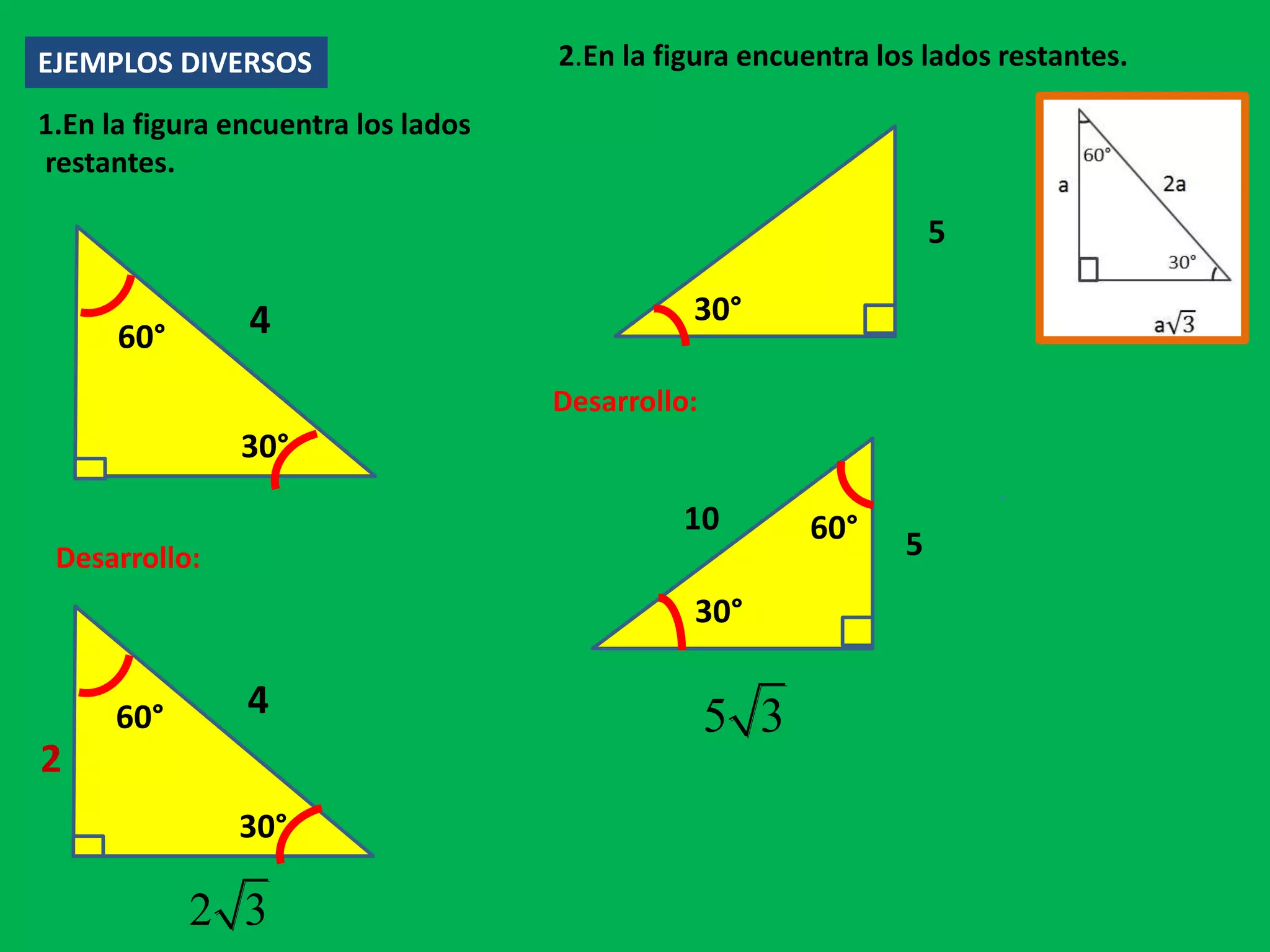
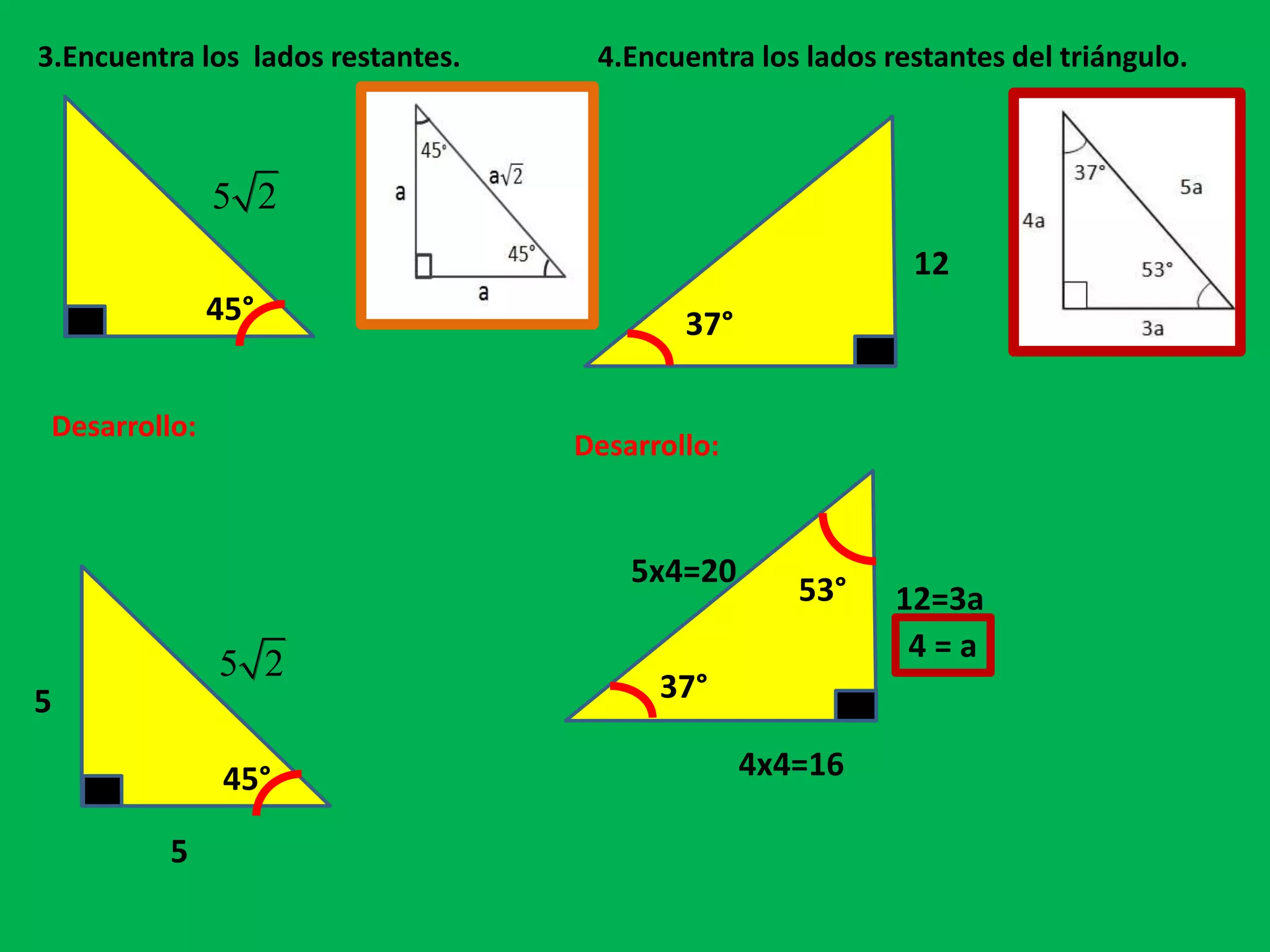
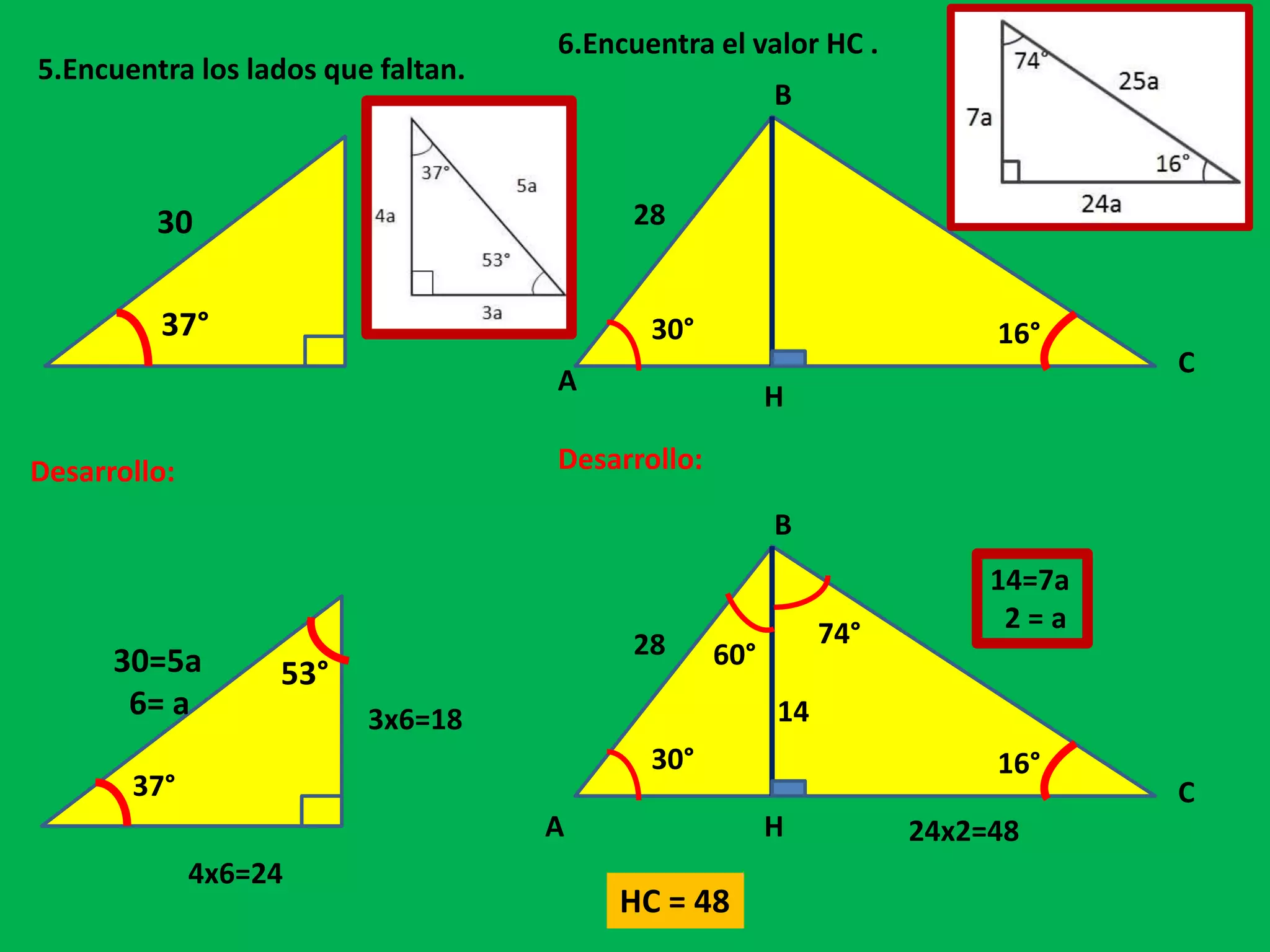
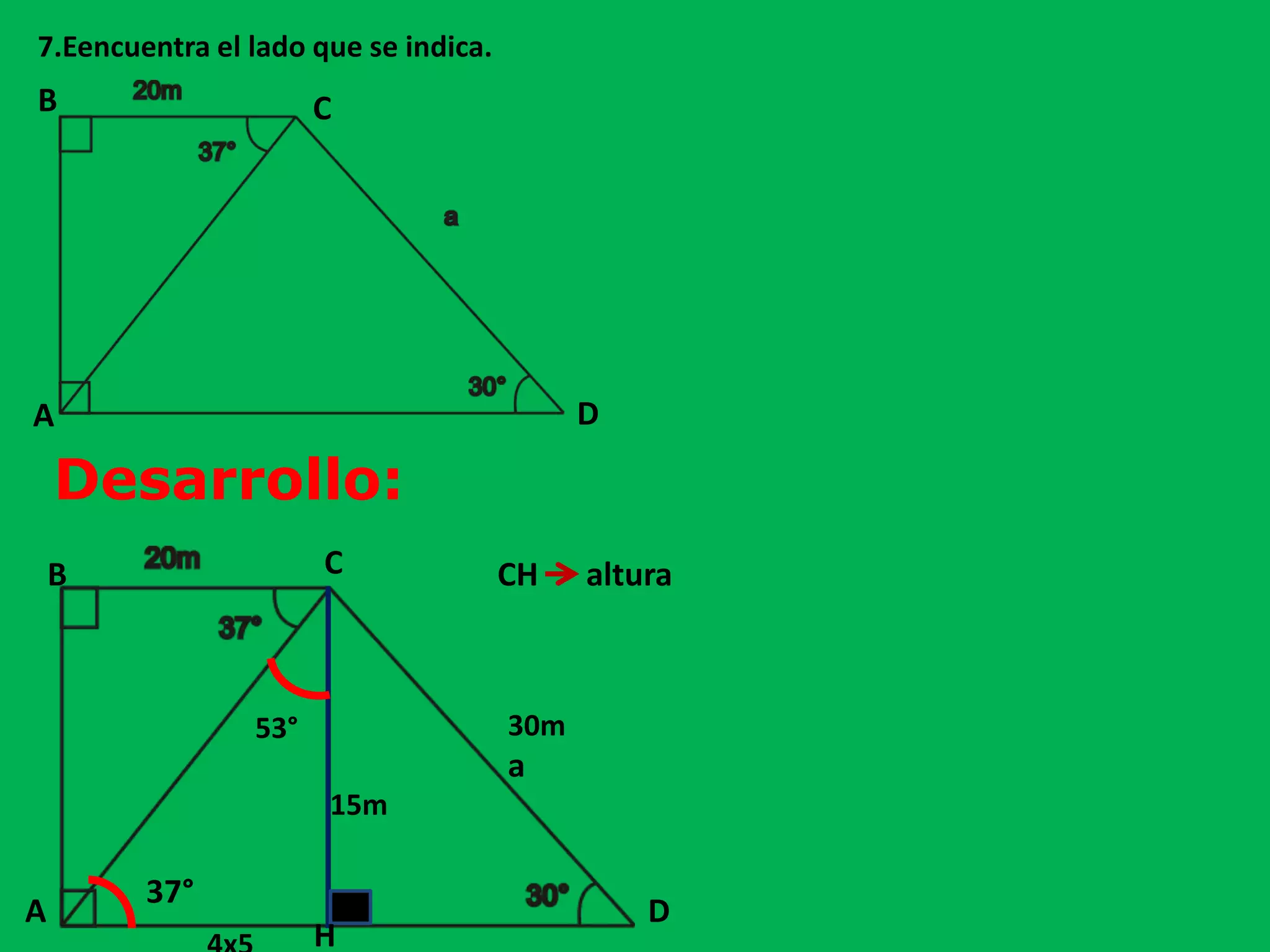
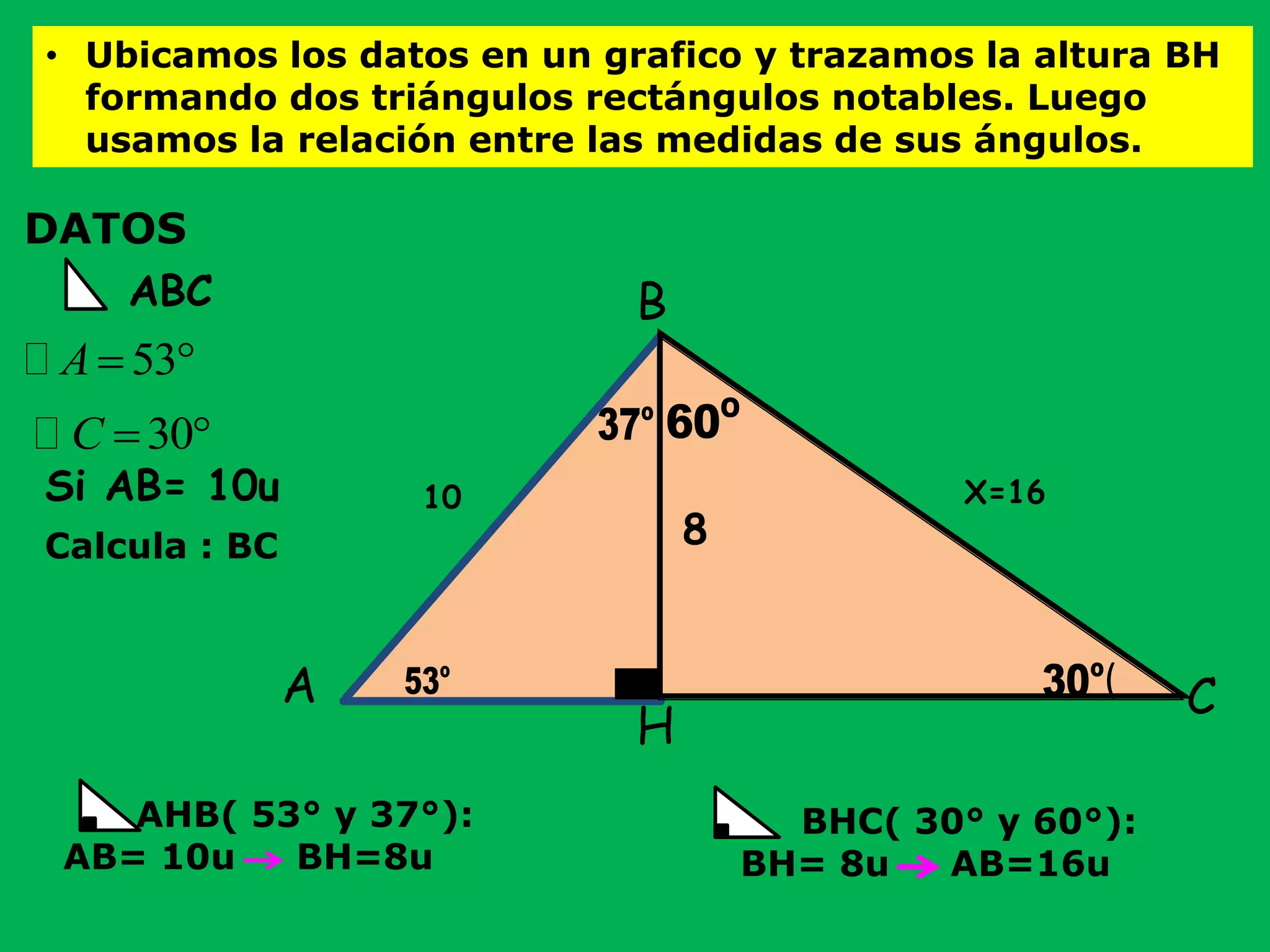
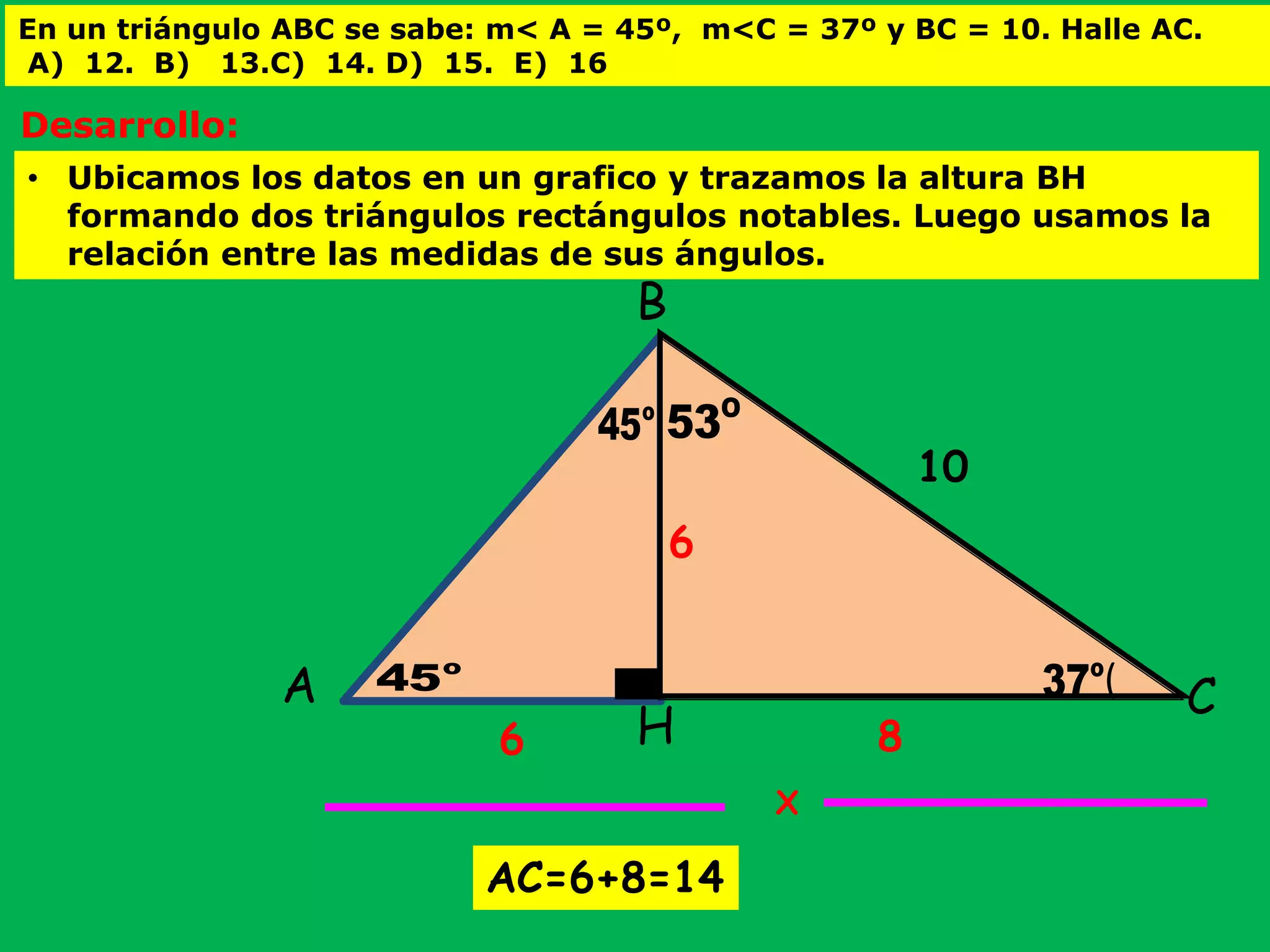
Este documento presenta información sobre triángulos rectángulos y sus propiedades. Explica que los triángulos rectángulos tienen relaciones entre la longitud de sus lados y los ángulos opuestos, y proporciona ejemplos de triángulos notables. También muestra cómo usar estas propiedades para calcular lados desconocidos en problemas de triángulos rectángulos.

1. Has un clic
en la figura

2. Has un clic
en la figura

3. TRIÁNGULO
RECTÁNGULO

2
b 2
a
c2

4. Se usa mucho
para calcular la
altura de
edificios, postes,
árboles etc.
Solo necesitas
dos datos para
encontrar el
tercero
PITÁGORAS

5. Es el único
polígono
que no se
deforma
El triángulo es la forma
geométrica más estable, ya
que no se deforma al actuar
fuerzas externas sobre él.
Esta es la razón por la que se utiliza la triangulación
para aportar mayor rigidez a las estructuras.

6. o
37
o
53
(
3k
5k
4k

7. Tienen aplicaciones en muchas ramas
de las ciencias y la vida cotidiana, sirve
para saber alturas de montañas,
edificios o cualquier construcción,
distancias, anchuras de ríos y lagos, en
fin, toda aplicación que tenga que ver
con longitudes.
Los triángulos rectángulos poseen
propiedades que ayudan a los
ingenieros a construir puentes, edificios,
en fin.

8. ((
En ciertos triángulos
rectángulos existe una
relación entre la amplitud
de sus ángulos y la
longitud de sus lados
opuestos
Estas son las relaciones métricas de
triángulos notables más representativos:
o
45
o
45
o
30
k 2k
k
O
60 2k
3k
k

9. (
o
37
o
53
(
74°
16°
7k
25k
24k
3k
5k
4k

10. EJEMPLOS DIVERSOS
1.En la figura encuentra los lados
restantes.
4
30°
60°
Desarrollo:
4
30°
60°
2
2 3
2.En la figura encuentra los lados restantes.
5
30°
Desarrollo:
5
30°
60°10
5 3

11. 3.Encuentra los lados restantes.
45°
5 2
45°
5 2
Desarrollo:
5
5
4.Encuentra los lados restantes del triángulo.
12
37°
12=3a
37°
Desarrollo:
4 = a
53°
4x4=16
5x4=20

12. 5.Encuentra los lados que faltan.
37°
30
Desarrollo:
37°
30=5a
6= a
53°
3x6=18
4x6=24
6.Encuentra el valor HC .
A
B
C
H
30°
28
16°
A
B
C
H
30°
28
16°
Desarrollo:
60°
74°
14
24x2=48
HC = 48
14=7a
2 = a

13. 7.Eencuentra el lado que se indica.
Desarrollo:
37°
15m
30m53°
a
B C
DA
B
A D
C
H
CH altura

14. En un triangulo ABC, los ángulos A y C miden
53° y 30 respectivamente,
Si AB= 10u, calcula la medida del lado BC
EJEMPLO :

15. • Ubicamos los datos en un grafico y trazamos la altura BH
formando dos triángulos rectángulos notables. Luego
usamos la relación entre las medidas de sus ángulos.
DATOS
ABC
( (o
30
O
60o
37
o
53A C
B
H
53A 
30C  
Si AB= 10u
Calcula : BC 8
10
AHB( 53° y 37°):
AB= 10u BH=8u
BHC( 30° y 60°):
BH= 8u AB=16u
X=16

16. En un triángulo ABC se sabe: m< A = 45º, m<C = 37º y BC = 10. Halle AC.
A) 12. B) 13.C) 14. D) 15. E) 16
( (o
37
O
53o
45
o
45A C
B
H
10
X
8
6
6
• Ubicamos los datos en un grafico y trazamos la altura BH
formando dos triángulos rectángulos notables. Luego usamos la
relación entre las medidas de sus ángulos.
Desarrollo:
AC=6+8=14