La mayoría de las variables aleatorias que se presentan en los estudios relacionados con las ciencias sociales, físicas y biológicas, por ejemplo, el peso de niños recién nacidos, talla de jóvenes de 18 años en una determinada región, son continuas y se distribuyen según una función de densidad , que tiene la siguiente expresión analítica

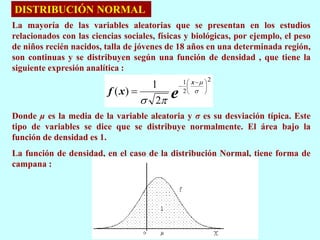
1. La mayoría de las variables aleatorias que se presentan en los estudios
relacionados con las ciencias sociales, físicas y biológicas, por ejemplo, el peso
de niños recién nacidos, talla de jóvenes de 18 años en una determinada región,
son continuas y se distribuyen según una función de densidad , que tiene la
siguiente expresión analítica :
Donde μ es la media de la variable aleatoria y σ es su desviación típica. Este
tipo de variables se dice que se distribuye normalmente. El área bajo la
función de densidad es 1.
La función de densidad, en el caso de la distribución Normal, tiene forma de
campana :
DISTRIBUCIÓN NORMAL
2
2
1
2
1
)
( e
x
x
f





 

 




2. Es un ejercicio interesante comprobar que ésta alcanza un único máximo
(moda) en  , que es simétrica con respecto al mismo, y por tanto
con lo cual en  coinciden la media, la mediana y la moda.
La mayor parte de la masa de probabilidad (área comprendida entre la curva
y el eje de abcisas) se encuentra concentrado alrededor de la media, y las
ramas de la curva se extienden asintóticamente a los ejes, de modo que
cualquier valor ``muy alejado" de la media es posible (aunque poco
probable).
La forma de la campana de Gauss depende de los parámetros  y  :
DISTRIBUCIÓN NORMAL
    2
1



 
 X
P
X
P
 indica la posición de la campana
(parámetro de centralización)
 será el parámetro de dispersión. Cuanto menor
sea, mayor cantidad de masa de probabilidad
habrá concentrada alrededor de la media

3.  





b
a
x
e
b
X
a
p
2
2 2
2
1
)
( 



Para una variable aleatoria X, que se distribuye normalmente con media : μ y
desviación típica: σ, la probabilidad de que la variable X esté comprendida
entre los valores a y b es el área oscura en la siguiente figura :
DISTRIBUCIÓN NORMAL
analíticamente se puede calcular así:

4. DISTRIBUCIÓN NORMAL
Como el cálculo de esta integral es laborioso, para calcular el área se realiza el
siguiente cambio de variable:




X
Z
Este cambio origina una distribución normal estándar de media μ = 0 y
desviación típica σ = 1 cuya función de densidad es :
e
t
z
f 2
2
2
1
)
(



2
2
1
2
1
)
( e
x
x
f





 

 



Y cuyos
valores se
tabulan :

5. Ejemplo 1:
Consideremos que el peso de los niños varones españoles en el momento del
nacimiento se distribuye normalmente.
Si sabemos que el peso medio en el momento de nacer son 3,25 kgs y la
desviación típica es de 0,82 kgs, ¿cúal es la probabilidad de que el peso de un
niño varón al nacer sea superior a 4 kgs?
Tipificamos la variable aleatoria X, peso de los niños al nacer.
En el proceso de tipificación, al valor de X=4, le corresponde el valor, z=0,9146 :
9146
.
0
82
.
0
25
.
3
4







X
z
4 0,9146
0

6. En la tabla de la distribución normal tipificada, buscamos el valor de α
correspondiente al valor de z=0,9146 ; la probabilidad de z > 0,9146 es,
18
,
0
)
9146
,
0
(
)
4
( 


 z
p
X
p

7. Ejemplo 2:
Según un estudio, la altura de los varones de cierta ciudad es una v.a. X, que
podemos considerar que se distribuye según una ley gaussiana de valor
esperado =175 cm y desviación típica =10 cm . Dar un intervalo para el que
tengamos asegurado que el 50% de los habitantes de la ciudad estén
comprendidos en él.
En este caso tenemos que buscar en la tabla de la N(0,1) que valor me deja el
25% de los datos hacia la derecha y el valor que me deja el 25 % a la izquierda,
de esta manera tenemos el 50% en los valores centrales.

8. El 50% de la población tiene
un peso comprendido en el
intervalo [168,25,181,75].
75
,
181
175
)
10
675
,
0
(
10
175
675
,
0 





 X
X
Buscamos el valor tipificado que
me da la Probabilidad de 0,25 en
la N(0,1) que es
aproximadamente 0,675
Por lo tanto si “destipificamos”
N(175, 10)
Como es simétrica la distribución,
el valor que nos deja el 25% por
debajo es -0,675
25
,
168
175
)
10
675
,
0
(
10
175
675
,
0 







 X
X

9. Se puede demostrar (teorema central del límite) que una v.a. discreta con
distribución binomial,
se puede aproximar mediante una distribución normal si n es suficientemente
grande y p no está ni muy próximo a 0 ni a 1. Como el valor esperado y la
varianza de X son respectivamente np y npq, la aproximación consiste en decir
que
El convenio que se suele utilizar para poder realizar esta aproximación es:
aunque en realidad esta no da resultados muy precisos a menos que realmente
n sea un valor muy grande y
DISTRIBUCIÓN NORMAL.
Aproximación de una Binomial a la Normal

10. Ejemplo. Durante cierta epidemia de gripe, enferma el 30% de la población. En
un aula con 200 estudiantes de Medicina, ¿cuál es la probabilidad de que al
menos 40 padezcan la enfermedad? Calcular la probabilidad de que haya 60
estudiantes con gripe.
La v.a. que contabiliza el número de alumnos que padece la gripe es
cuya media es =200x0,3=60 y cuya 2 =200x0,3x0x7=42
Realizar los cálculos con la ley binomial es muy engorroso, ya que intervienen
números combinatorios de gran tamaño, y potencias muy elevadas. Por ello
utilizamos la aproximación normal de X, teniendo en cuenta que se verifican las
condiciones necesarias para que el error sea aceptable:

11. Con una N(60; 6,48)
Tipificando
Buscamos
Por simetría
Por suceso contrario
Buscando en la tabla
09
,
3
48
,
6
60
40








X
z
)
09
,
3
(
)
09
,
3
( 


 z
P
z
P
)
09
,
3
(
1
)
09
,
3
( 


 z
P
z
P
999
,
0
001
,
0
1
)
09
,
3
(
1 



 z
P
)
09
,
3
(
)
40
( 


 z
P
x
P

12. Con una N(60; 6,48)
Tipificando
Buscamos
Por simetría
Buscando en la tabla
09
,
3
48
,
6
60
40








X
z
)
09
,
3
(
)
09
,
3
( 


 z
P
z
P
)
09
,
3
(
)
40
( 


 z
P
x
P

13. Tipificando
Buscamos
Por simetría
Buscando en la tabla
09
,
3
48
,
6
60
40








X
z
)
09
,
3
(
)
09
,
3
( 


 z
P
z
P
)
09
,
3
(
)
40
( 


 z
P
x
P