Probabilidades

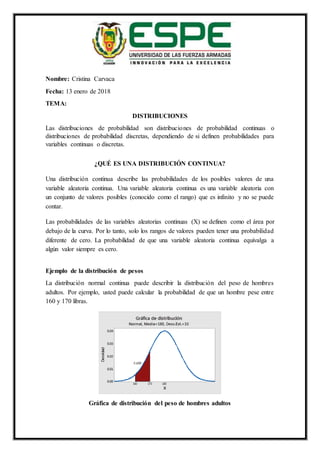
1. Nombre: Cristina Carvaca
Fecha: 13 enero de 2018
TEMA:
DISTRIBUCIONES
Las distribuciones de probabilidad son distribuciones de probabilidad continuas o
distribuciones de probabilidad discretas, dependiendo de si definen probabilidades para
variables continuas o discretas.
¿QUÉ ES UNA DISTRIBUCIÓN CONTINUA?
Una distribución continua describe las probabilidades de los posibles valores de una
variable aleatoria continua. Una variable aleatoria continua es una variable aleatoria con
un conjunto de valores posibles (conocido como el rango) que es infinito y no se puede
contar.
Las probabilidades de las variables aleatorias continuas (X) se definen como el área por
debajo de la curva. Por lo tanto, solo los rangos de valores pueden tener una probabilidad
diferente de cero. La probabilidad de que una variable aleatoria continua equivalga a
algún valor siempre es cero.
Ejemplo de la distribución de pesos
La distribución normal continua puede describir la distribución del peso de hombres
adultos. Por ejemplo, usted puede calcular la probabilidad de que un hombre pese entre
160 y 170 libras.
Gráfica de distribución del peso de hombres adultos

2. El área sombreada debajo de la curva en este ejemplo representa el rango de 160 a 170
libras. El área de este rango es 0.136; por lo tanto, la probabilidad de que un hombre
seleccionado aleatoriamente pese entre 160 y 170 libras es de 13.6%. Toda el área por
debajo de la curva equivale a 1.0.
Sin embargo, la probabilidad de que X sea exactamente igual a algún valor siempre es
cero, porque el área por debajo de la curva en un punto individual, que no tiene anchura,
es cero. Por ejemplo, la probabilidad de que un hombre pese exactamente 190 libras es
cero. Podría calcular una probabilidad diferente de cero de que un hombre pese más de
190 libras, menos de 190 libras o entre 189.9 y 190.1 libras, pero la probabilidad de que
pese exactamente 190 libras es cero.
¿QUÉ ES UNA DISTRIBUCIÓN NORMAL?
Se trata, sin duda, del modelo continuo más importante en estadística, tanto por su
aplicación directa, veremos que muchas variables de interés general pueden describirse
por dicho modelo, como por sus propiedades, que han permitido el desarrollo de
numerosas técnicas de inferencia estadística. En realidad, el nombre de Normal proviene
del hecho de que durante un tiempo se creyó, por parte de médicos y biólogos, que todas
las variables naturales de interés seguían este modelo.
Su función de densidad viene dada por la fórmula:
que, como vemos, depende de dos parámetros μ (que puede ser cualquier valor real) y σ
(que ha de ser positiva). Por esta razón, a partir de ahora indicaremos de forma
abreviada que una variable X sigue el modelo Normal así: X ~ N(μ, σ). Por ejemplo, si
nos referimos a una distribución Normal con μ = 0 y σ = 1 lo abreviaremos N(0, 1).
De hecho, a este modelo, también se le conoce con el nombre de distribución
gaussiana.
Propiedades del modelo Normal
1. Su esperanza es μ.
2. Su varianza es σ2 y, por tanto, su desviación típica es σ.
3. Es simétrica respecto a su media μ, como puede apreciarse en la representación
anterior.
4. Media, moda y mediana coinciden (μ).
5. Cualquier transformación lineal de una variable con distribución Normal seguirá
también el modelo Normal. Si X ~ N(μ, σ) y definimos Y = aX + b (con a ≠ 0),

3. entonces Y ~ N(aμ + b, |a|σ). Es decir, la esperanza de Y será aμ + b y su
desviación típica, |a|σ.
6. Cualquier combinación lineal de variables normales independientes sigue
también una distribución Normal. Es decir, dadas n variables aleatorias
independientes con distribución Xi ~ N(μi, σi) para i = 1, 2, ..., n la combinación
lineal: Y = anXn + an−1Xn−1+ ... + a1X1 + a0 sigue también el modelo Normal:
¿QUÉ ES UNA DISTRIBUCIÓN EXPONENCIAL?
A pesar de que la distribución Normal puede utilizarse para resolver muchos problemas
en ingeniería y ciencias, existen aún numerosas situaciones que requieren diferentes tipos
de funciones de densidad, tales como la exponencial y la gamma y algunas otras como la
weibull, etc., etc., de momento solo trataremos sobre el uso de la exponencial.
Resulta que la exponencial es un caso especial de la distribución gamma, ambas tienen
un gran número de aplicaciones. Las distribuciones exponencial y gamma juegan un papel
importante tanto en teoría de colas como en problemas de confiabilidad. El tiempo entre
las llegadas en las instalaciones de servicio y el tiempo de falla de los componentes y
sistemas eléctricos, frecuentemente involucran la distribución exponencial. La relación
entre la gamma y la exponencial permite que la distribución gamma se utilice en tipos
similares de problemas.
La variable aleatoria x tiene una distribución exponencial, con parámetro b, si su función
de densidad es:
, x > 0 ; f(x) = 0 en cualquier otro caso
donde b > 0
La media y la variancia de la distribución exponencial son:
m = b y s2 = b2
Relación con el proceso de Poisson.
Las aplicaciones más importantes de la distribución exponencial son aquellas situaciones
en donde se aplica el proceso de Poisson, es necesario recordar que un proceso de Poisson
permite el uso de la distribución de Poisson. Recuérdese también que la distribución de
Poisson se utiliza para calcular la probabilidad de números específicos de “eventos”
durante un período o espacio particular. En muchas aplicaciones, el período o la cantidad
de espacio es la variable aleatoria. Por ejemplo un ingeniero industrial puede interesarse
en el tiempo T entre llegadas en una intersección congestionada durante la hora de salida
de trabajo en una gran ciudad. Una llegada representa el evento de Poisson.
La relación entre la distribución exponencial (con frecuencia llamada exponencial
negativa) y el proceso llamado de Poisson es bastante simple. La distribución de Poisson

4. se desarrolló como una distribución de un solo parámetro l, donde l puede interpretarse
como el número promedio de eventos por unidad de “tiempo”. Considérese ahora la
variable aleatoria descrita por el tiempo que se requiere para que ocurra el primer evento.
Mediante la distribución de Poisson, se encuentra que la probabilidad de que no ocurran
en el espacio hasta el tiempo t está dada por:
;
Ahora puede utilizarse lo anterior y hacer que X sea el tiempo para el primer evento de
Poisson. La probabilidad de que el período hasta que ocurre el primer evento de Poisson
exceda x es la misma que la probabilidad de que no ocurra un evento de Poisson en x.
Esto último por supuesto está dado por . Como resultado,
P(X ³ x) =
Entonces, la función de distribución acumulada para x es:
P(0£ X £ x) = 1 -
Ahora, con objeto de que se reconozca la presencia de la distribución exponencial, puede
derivarse la distribución acumulada anterior para obtener la función de densidad:
f(x) =
La cual es la función de densidad de la distribución exponencial con .
Nótese que la media de la distribución exponencial es el parámetro , el recíproco del
parámetro en la distribución de Poisson. El lector debe recordar que con frecuencia se
dice que la distribución de Poisson no tiene memoria, lo cual implica que las ocurrencias
en períodos de tiempo sucesivos son independientes. Aquí el parámetro importante es
el tiempo promedio entre eventos. En teoría de la confiabilidad, donde la falla de un
equipo concuerda con el proceso de Poisson, recibe el nombre de tiempo promedio
entre fallas. Muchas descomposturas de equipo siguen el proceso de Poisson, y entonces
la distribución exponencial es aplicable.
En el siguiente ejemplo se muestra una aplicación simple de la distribución exponencial
en un problema de confiabilidad. La distribución binomial también juega un papel
importante en la solución.
¿QUÉ ES UNA DISTRIBUCIÓN T DE STUDENT?
Sean X1, X2,…, Xn, X; n +1 variables aleatorias N (0, σ) independientes entre sí. La
variable tn:
Se denomina t de Student con n grados de libertad. Dividiendo en el segundo miembro
numerador y denominador por σ, tenemos:

5. Con Z es N (0, 1) y cn
2 es una c2de Pearson con n grados de libertad.
La función de densidad de esta t de Student con n grados de libertad es:
Siendo b (p, q) la función beta:
Al observar la distribución t de Student con n grados de libertad, observamos:
a) El campo de variabilidad de tn es toda la recta real.
b) Su distribución depende sólo del parámetro n.
c) Conforme n va aumentado, la curva que representa a la función de densidad va
siendo cada vez más apuntada, coincidiendo en el límite, cuando n ®¥ con la curva
normal tipificada.
d) No depende de σ
e) Es simétrica respecto del eje de ordenadas OY.
f) En el muestreo al tomar muestras de tamaño n de media y varianza s2 de una
población N (μ, σ), la variable
Sigue una t de Student con n-1 grados de libertad. Esta propiedad es muy utilizada en la
estimación y el contraste de hipótesis sobre la media de la población μ.
g) Está tabulada para diferentes valores de n. Para el uso de la tabla consideramos
valores de ta,n (punto crítico) tales que el área bajo la curva a la derecha de este valor es
igual a α (nivel de significación). Es decir:
Sólo se encuentran valores de t ³ 0 (o áreas α menores o iguales que 0.5). Para valores de
t £ 0 se puede obtener por simetría.

6. Bibliografía
https://support.minitab.com/es-mx/minitab/18/help-and-how-to/probability-
distributions-and-random-data/supporting-topics/basics/continuous-and-discrete-
probability-distributions/
http://www.ub.edu/stat/GrupsInnovacio/Statmedia/demo/Temas/Capitulo4/B0C4m1t4.h
tm
http://www.itchihuahua.edu.mx/academic/industrial/sabaticorita/_private/03Distribucio
n%20Exponencial.htm
http://www.juntadeandalucia.es/averroes/centros-
tic/14002996/helvia/aula/archivos/repositorio/250/295/html/estadistica/dcontinuas.htm#
Cuatro