1. El documento presenta la biografía y experiencia profesional de Álvaro García Meseguer, autor del libro "Estructuras de Hormigón Armado". García Meseguer es doctor ingeniero, profesor e investigador con una amplia experiencia en el campo del hormigón.
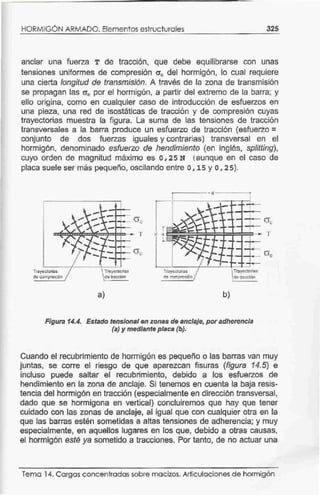
2. El libro consta de 13 temas sobre diferentes elementos estructurales de hormigón armado como vigas, soportes, placas, cimentaciones y otros. Cada tema incluye conceptos teóricos, ejemplos y ejercicios de autocomp


































































![76 Álvaro García Meseguer
Para la comprobación de la capacidad resistente de las bielas en el
estado límite último, deberán adoptarse los siguientes valores reducidos
f 1cd de la resistencia del hormigón:
• Si la biela de hormigón pertenece a una zona sometida a un estado
de compresión uniaxial (como es el caso del cordón comprimido de
una viga sometida a flexión), se tomará:
[
fck ] 2
f 1cd = 0,85 1 -
250
fcd con f c k en N/mm
• Cuando existan fisuras paralelas a las bielas, cuya abertura esté
controlada por armadura transversal suficientemente anclada (como
es el caso del alma de una viga sometida a esfuerzo cortante, así
como del ala de compresión de una viga T sometida a esfuerzo
rasante en su unión con el nervio), se tomará:
f 1cd =O, 60 f cd
• Cuando existan fisuras paralelas a las bielas de gran abertura (como
es el caso de elementos sometidos a tracción, así como del ala de
tracción de una viga T sometida a esfuerzo rasante), se tomará:
f 1cd =O, 4 O fcd
• En el caso particular del punzonamiento (ver Tema 6) se tomará:
f1cd= 0,30 f cd
Las limitaciones mencionadas responden al hecho de que la capacidad
resistente del hormigón se ve apreciablemente reducida a causa de su
estado tensional y, en especial, por la presencia de fisuras paralelas a
la dirección de las compresiones, tanto más cuanto mayor sea la
anchura de aquéllas (recuérdese el efecto de engranamiento de áridos,
tanto menor cuanto más ancha sea la fisura).
Tema 3. Mé1odo de bielas y tirantes. Aplicaciones](https://image.slidesharecdn.com/estructurasdehormigonarmado-150501175559-conversion-gate02/85/Estructuras-de-hormigon-armado-70-320.jpg)
























































![134 Álvaro García Meseguer
Se supone que las cargas crecen proporcionalmente, de forma que las
que actúan al producirse la rotura quedan fijadas por un único
parámetro incógnita, que llamaremos genéricamente carga de rotura.
Son también incógnitas la posición de los ejes de rotación de los n
trozós de placa y los giros de n - 1 de ellos (puesto que todo ello es lo
que fija la configuración de rotura, según se ha visto en el apartado
5. 1.3), así como las reacciones de los apoyos de la placa (ya que los
momentos flector y torsor en las líneas de rotura son conocidos en
función de las armaduras de la placa).
En un trozo de placa apoyada según un lado recto, el eje de rotación es
conocido, pero se desconoce el valor de la resultante de las reacciones
de apoyo y su punto de paso. Si el trozo está apoyado en un punto, el
eje de apoyo y la resultante pasarán por dicho punto, pero se
desconoce la dirección del eje y el valor de la resultante. Si el trozo no
está apoyado, no es necesario calcular la resultante de las reacciones
de apoyo, pero se desconoce por completo la posición del eje de
rotación .
Resumiendo, las incógnitas son: la carga de rotura (1); los giros (n-1),
y los ejes de giro y reacciones apoyo de los trozos (2 •n). En total 3 · n,
es decir, tantas como ecuaciones.
Es posible, por tanto, al menos teóricamente, determinar la
configuración de rotura y la carga de rotura, aunque el cálculo resulta,
en la práctica, muy laborioso. En muchos casos, sin embargo, se
simplifica por la existencia de simetrías en la placa.
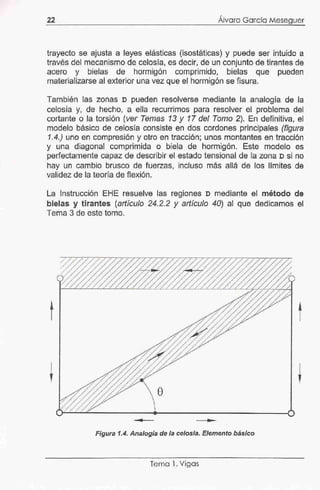
Como ejemplo, sea una placa rectangular (figura 5. 12) apoyada en tres
bordes y libre en el cuarto, sometida a una carga uniforme q y con
armadura isótropa (es decir, armaduras iguales en dos direcciones
perpendiculares). En este caso la configuración de rotura ha de ser la
indicada, ya que los ejes de rotación son los bordes. Debido a la
simetría, dicha configuración queda definida en función de un único
parámetro x. Las líneas de rotura son todas positivas.
Para no tener que calcular las reacciones de apoyo, como ecuación de
equilibrio del trozo A se elige la de momentos alrededor de su eje de
apoyo:
m , b - q . r(b - x) a . a + ~ , X . ~]
- 2 4 2 2 6
Tema 5. Método de laslíneas de rotura](https://image.slidesharecdn.com/estructurasdehormigonarmado-150501175559-conversion-gate02/85/Estructuras-de-hormigon-armado-127-320.jpg)
















![152 Álvaro García Meseguer
6.3.
PLACAS SIN ARMADURA DE
PUNZONAMIENTO
6.3.1 . Comprobación
Una placa sometida a una carga o reacción concentrada actuando en
una pequeña zona no necesita armadura de punzonamiento si se
verifica la siguiente condición:
"!;' • =
!'ª
[1]
con los siguientes significados:
'tsd tensión nomihal de cálculo en el perímetro crítico.;
Fsd esfuerzo de punzonamiento de cálculo (carga o reacción menos la
carga dentro de un perímetro situado a h/2 de la sección del
soporte o área cargada. En zapatas, dentro del perímetro crítico);
coeficiente que tiene en cuenta la excentricidad de la carga, si
existe (si no existe, 13 =1):
para soportes interiores: f3 =1, 1.5
para soportes de borde: f3 =1, 4 o
para soportes de esquina~ f3 = 1, 5 o
para soportes de borde
o esquina con perímetro
u 1* (figura 6.4): f3 =1, oo;
u 1 perímetro crítico, definido en el apartado 6.2;
d canto útil medio
de la losa: d = (<ixc + dy) / 2;
Tema 6. !punzonamiento](https://image.slidesharecdn.com/estructurasdehormigonarmado-150501175559-conversion-gate02/85/Estructuras-de-hormigon-armado-144-320.jpg)


















































































































































































































































![,
HORMIGON ARMADO. Elementos estructurales
Peso propio +peso
1err~no.
cr.max = 13.7
El esfuerzo cortante vale:
f T
-¡
0:5
,'!---.--.---,----' J
'~
' l--'---'-
0.30 _J
~------- 1.00 -------
Figura 16.29
403
Peso. pr0pio + peso
térreno
Vd = 1,6 · 0,5 (13,7 - 1,2 - 0,9) = 9,28 t
Finalmente, para el talón, si trabajamos con la distribución
triangular de tensiones, sale un poquito latoso. Es mejor trabajar
con la rectangular que, según vimos, conduce a cr = 10, 3 t/m2
extendida en 1, 3 o m a partir del borde A (en realidad, la puntera
podía haberse calculado con esta cr también, en vez de la máxima
triangular). En el otro sentido actúa el peso del relleno y el peso
propio, que pueden más.
- 1,6
1 2
• o,s· . 2,4
2
1 2
. 3,5 . 1 8
+ - -- --'- - 0,3 . 10,3 . 0,15
2
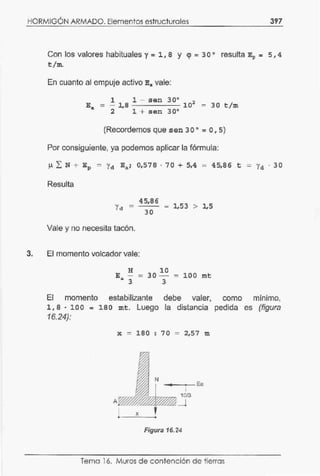
Md - 1,6 · 3,29 - 5;27 mt
Vd = 1,6 · (1 · 0,5 · 2,4 + 1 · 3,5 · 1,8 - 0,3 · 10,3] -
= 1,6 . 4,4 = 7,04 t
Tema 16. Muros de contención de tierras](https://image.slidesharecdn.com/estructurasdehormigonarmado-150501175559-conversion-gate02/85/Estructuras-de-hormigon-armado-389-320.jpg)