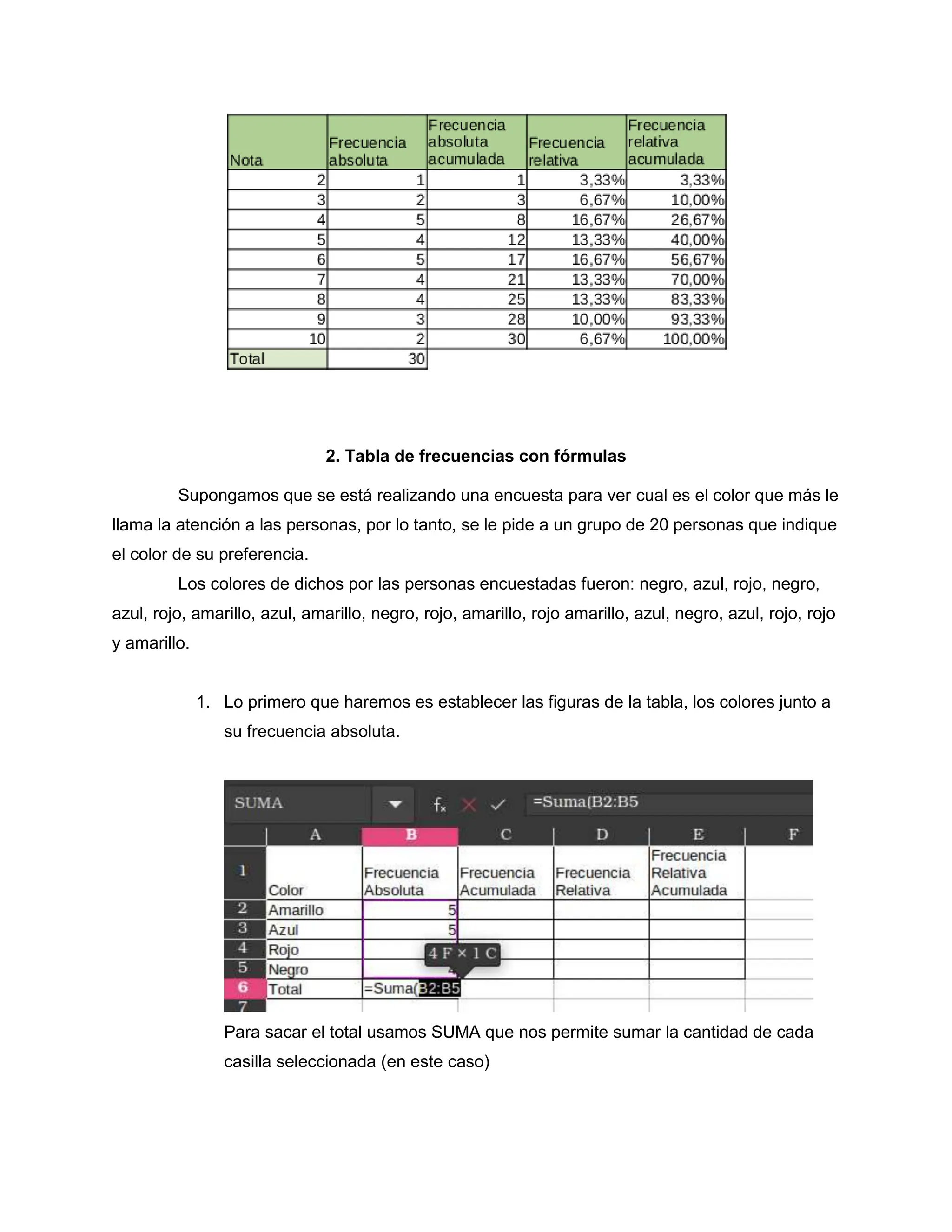
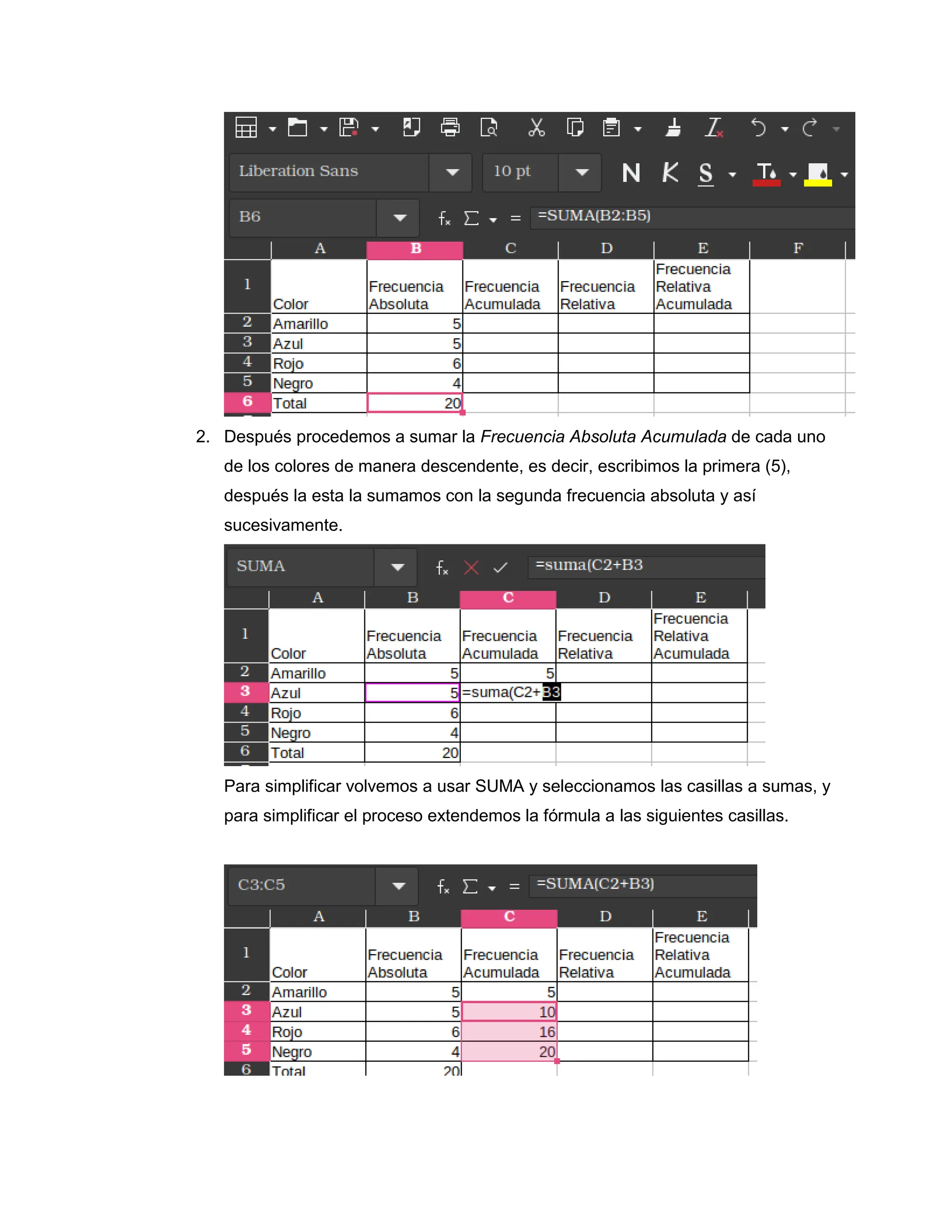
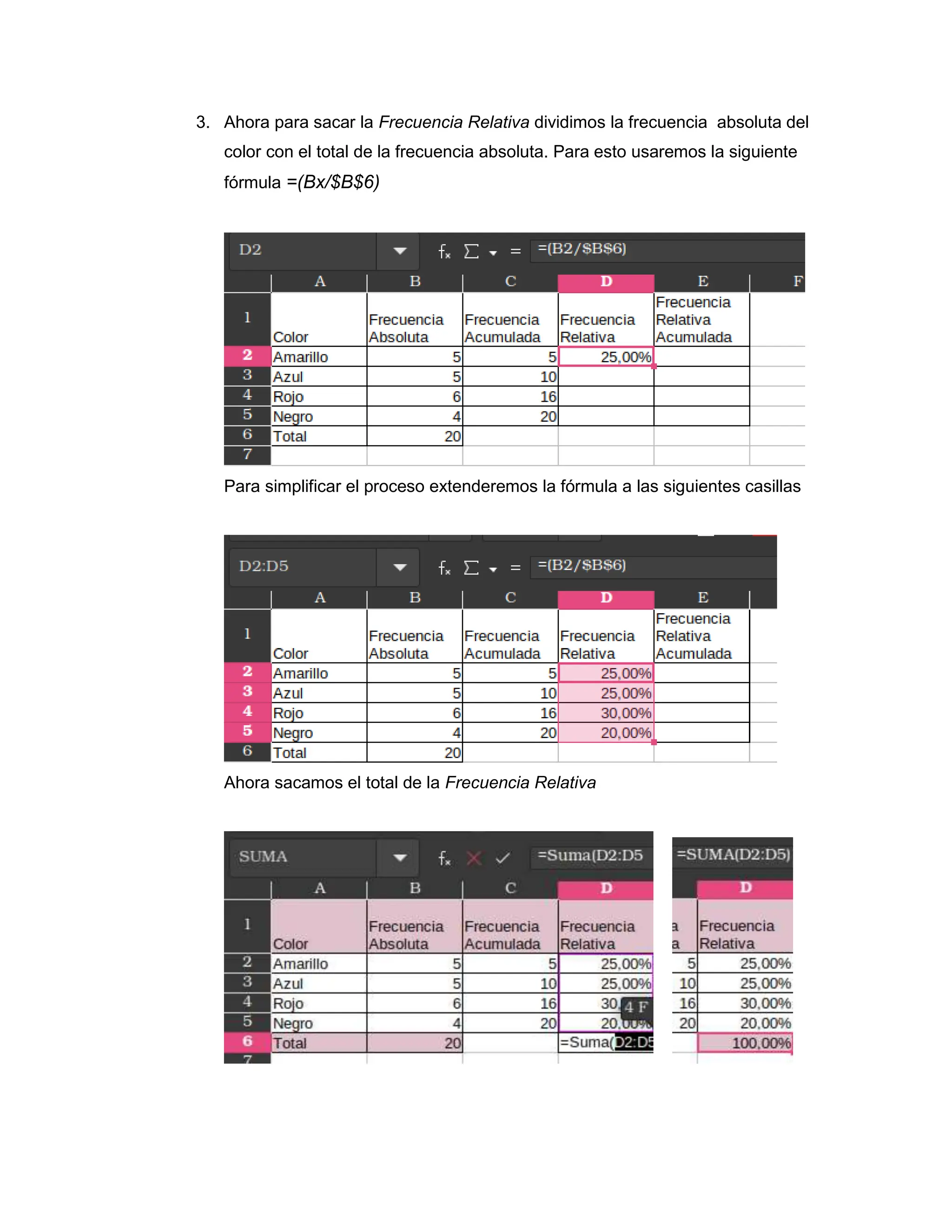
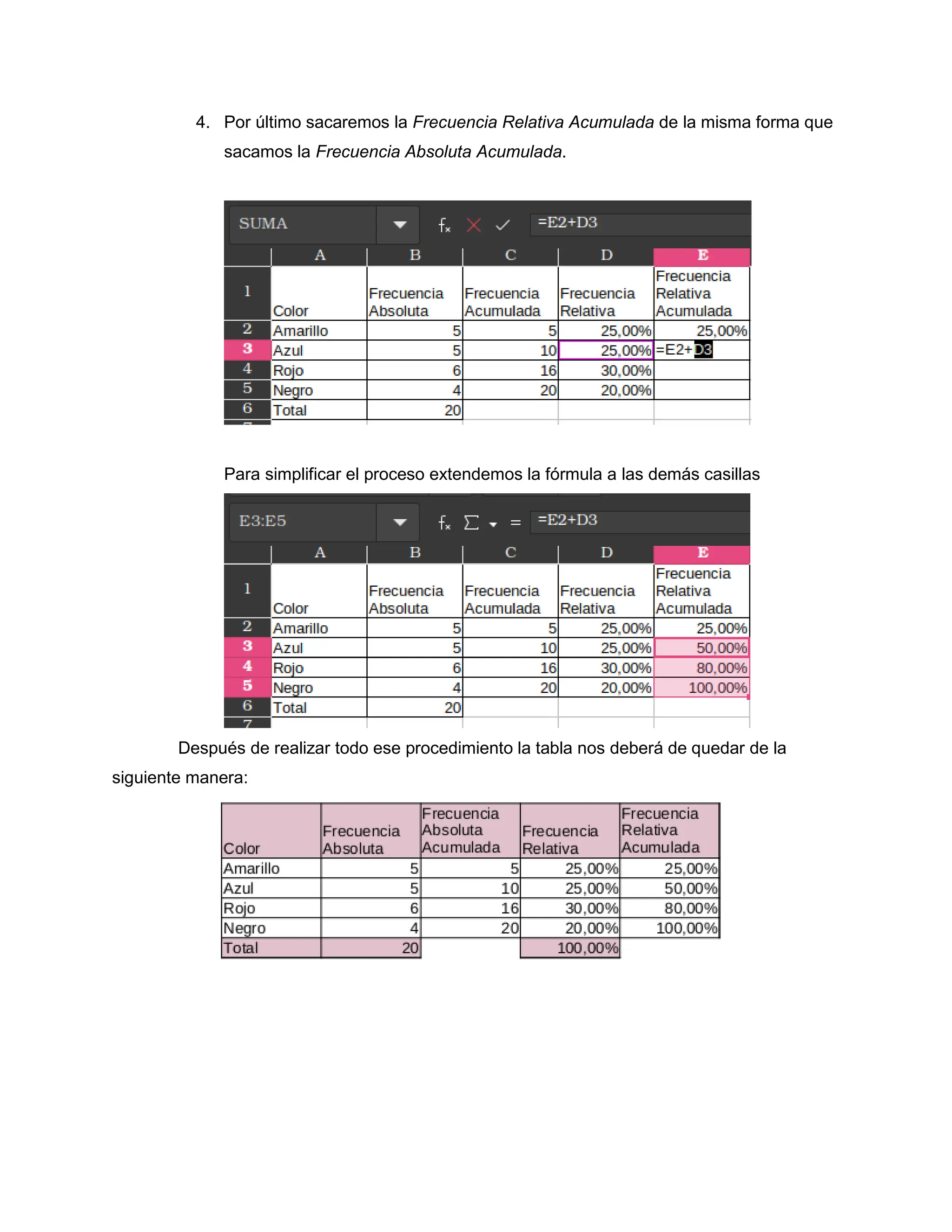
El documento aborda conceptos básicos de estadística, la ley de Sturges y la elaboración del diagrama de Pareto, herramientas fundamentales para el análisis de datos y la toma de decisiones. Se presentan explicaciones detalladas sobre cómo crear tablas de frecuencias, aplicar la ley de Sturges para histogramas, y utilizar el diagrama de Pareto para priorizar problemas. Las conclusiones destacan la importancia de estas metodologías en diversos campos, incluyendo la gestión de calidad y la eficiencia en la toma de decisiones.