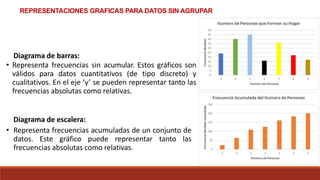
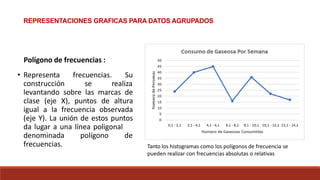
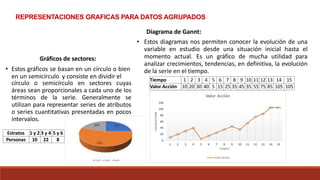
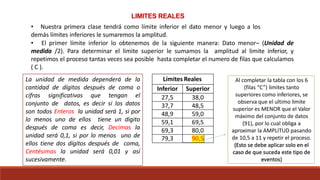
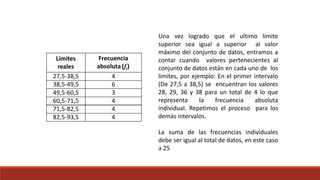
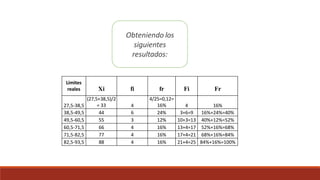
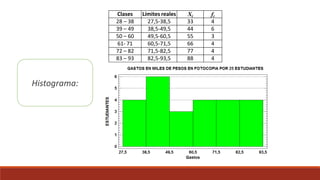
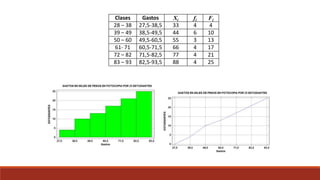
Este documento describe diferentes tipos de representaciones gráficas de datos, incluyendo diagramas de barras, diagramas de escalera, polígonos de frecuencias e histograma para datos sin agrupar. También describe gráficos de sectores y diagramas de Gantt para datos agrupados, así como los pasos para construir una tabla de frecuencias agrupadas.

1. REPRESENTACIONES GRAFICAS DE LA INFORMACIÓN
• Las representaciones gráficas
de los datos ofrecen una
idea más intuitiva y más fácil
de interpretar de un
conjunto de datos sometidos
a investigación. Por ello las
representaciones gráficas se
convierten en un medio muy
eficaz para el análisis ya que
las regularidades se
recuerdan con más facilidad
cuando se observan
gráficamente.
gráficas para datos sin
gráficas para datos
Se divide en dos:
• Representaciones
agrupar
• Representaciones
agrupados
ad 1

2. REPRESENTACIONES GRAFICAS PARA DATOS SIN AGRUPAR
Diagrama de barras:
• Representa frecuencias sin acumular. Estos gráficos son
válidos para datos cuantitativos (de tipo discreto) y
cualitativos. En el eje ‘y’ se pueden representar tanto las
frecuencias absolutas como relativas.
Diagrama de escalera:
• Representa frecuencias acumuladas de un conjunto de
datos. Este gráfico puede representar tanto las
frecuencias absolutas como relativas.

3. Polígono de frecuencias :
• Representa frecuencias. Su
construcción se realiza
levantando sobre las marcas de
clase (eje X), puntos de altura
igual a la frecuencia observada
(eje Y). La unión de estos puntos
da lugar a una línea poligonal
denominada polígono de
frecuencias. Tanto los histogramas como los polígonos de frecuencia se
pueden realizar con frecuencias absolutas o relativas
REPRESENTACIONES GRAFICAS PARA DATOS AGRUPADOS

4. Gráficos de sectores:
• Estos gráficos se basan en un círculo o bien
en un semicírculo y consiste en dividir el
círculo o semicírculo en sectores cuyas
áreas sean proporcionales a cada uno de los
términos de la serie. Generalmente se
utilizan para representar series de atributos
o series cuantitativas presentadas en pocos
intervalos.
ad 1
Diagrama de Gannt:
• Estos diagramas nos permiten conocer la evolución de una
variable en estudio desde una situación inicial hasta el
momento actual. Es un gráfico de mucha utilidad para
analizar crecimientos, tendencias, en definitiva, la evolución
de la serie en el tiempo.
Tiempo 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
Valor Acción 10 20 30 40 5 15 25 35 45 35 55 75 85 105 105
Estratos 1 y 2 3 y 4 5 y 6
Personas 10 22 8
REPRESENTACIONES GRAFICAS PARA DATOS AGRUPADOS

5. TABLA DE FRECUENCIAS DE DATOS
AGRUPADOS
Otra posibilidad de organizar datos es agruparlos en intervalos (llamados intervalos de clase o,
simplemente, clases). Los datos que organizados en tablas de frecuencias agrupadas se denominan
generalmente datos agrupados.
• Este es un ejemplo de una tabla de frecuencias
agrupada y 10-14 y 15-19 son ejemplos de clases.
En ella se presentan las distribuciones de
frecuencia para los datos de tiempo de auditorias
de fin de año.
TIEMPO DE AUDITORIA EN
DIAS
FRECUENCIA
10 - 14 4
15 - 19 8
20 - 24 5
25 - 29 2
30 - 34 1

6. CONCEPTOS BÁSICOS A UTILIZAR
INTERVALOS DE CLASE: Son grupos pequeños de datos de igual tamaño.
Se puede construir intervalos de clase, cerrados o intervalos de clase
semi abiertos. Un intervalo cerrado es cuando el limite superior de una
clase no es el límite superior de una clase es el limite inferior de una
clase siguiente.
LIMITE DE CLASES: Los intervalos de clase tienen límites: un límite
inferior y un límite suoerior.
AMPLITUD O ANCHO DE CLASE: es la distancia entre el límite superior o
inferior.
N= Número de datos de la muestra o de la población.
MARCA DE CLASE: es el punto medio de cada uno de los intervalos de
clase.
Límite inferior
Límite superior
Intervalo cerrado
Intervalos semi-abiertos

7. Las clases de frecuencias agrupadas poseen límites de clase.
En nuestro ejemplo anterior, en la clase 10-14, a 10 se le llama límite inferior de clase y a 14,
límite superior de clase. La distancia entre cualquiera de dos límites superiores consecutivos o
entre cualquiera de dos límites inferiores consecutivos es llamada amplitud de clase. La amplitud
de cada clase en la tabla anterior es 5. Una posible forma de construir la tabla de datos agrupados
seria la siguiente: (A continuación veremos como se elabora)

8.  Ordenar losdatosde menor amayor.
 Determinar el valormínimo yelvalormásalto de los datos.
 Calcular el Rango(R): se obtiene restando el valor máximo menos el valor mínimo de los
datos.
R=valormáximo-valor mínimo.
 Calcular el número de clases o intervalo (K):el número de clases debe estar expresado en el
enunciado del ejercicio, de no ser así se debe calcular mediante alguna de las siguientes
fórmulas:
K=1+3.332(log.N)
REGLA DE STURGES
N es el número de datos
K=√N
PASOS PARA CONSTRUIR UNA DISTRIBUCIÓN DE FRECUENCIAS CON DATOS
AGRUPADOS

9. EJEMPLO
Los datos anotados representan los totales, en miles de pesos, gastados en fotocopias por
una muestra de 25 estudiantes durante un semestre.
29 91 77 72 39 47 64 84 88 57 28 63 38
42 36 72 69 68 41 52 39 84 45 52 72
Solución
Clases: 𝑐 = 1 + 3,322 log 𝑛 = 1 + 3,322 log 25 = 5,61 ≈ 6
Amplitud: A = 𝑅
= 63
= 10,5
𝑐 6
Construya una tabla de frecuencias agrupadas usando la regla de Sturges.
1. Determinar el rango R, que es la diferencia entre las medidas mayor y menor. (En
nuestro ejemplo son el 91 y el 28)
2. Aplicar la regla de Sturges para determinar el numero de filas de la tabla de
frecuencias o del numero de clases. (Siempre se aproxima a su entero mas cercano)
3. Posteriormente determinamos la amplitud de clase A se encuentra como se muestra
en el siguiente recuadro.
Rango: R = Dato mayor – Dato menor = 91 – 28 = 63 La amplitud se aproxima
inicialmente al numero de dígitos
que tengan los limites (En este
ejemplo los limites tendrán
decimas por eso la A = 10,2)

10. • Nuestra primera clase tendrá como límite inferior el dato menor y luego a los
demás límites inferiores le sumaremos la amplitud.
• El primer límite inferior lo obtenemos de la siguiente manera: Dato menor– (Unidad de
medida /2). Para determinar el limite superior le sumamos la amplitud al limite inferior, y
repetimos el proceso tantas veces sea posible hasta completar el numero de filas que calculamos
( C ).
La unidad de medida dependerá de la
cantidad de dígitos después de coma o
cifras significativas que tengan el
conjunto de datos, es decir si los datos
son todos Enteros la unidad será 1, si por
lo menos uno de ellos tiene un digito
después de coma es decir, Decimas la
unidad será 0,1, si por lo menos uno de
ellos tiene dos dígitos después de coma,
Centésimas la unidad será 0,01 y así
sucesivamente.
Al completar la tabla con los 6
(filas “C”) limites tanto
superiores como inferiores, se
observa que el ultimo limite
superior es MENOR que el Valor
máximo del conjunto de datos
(91), por lo cual obliga a
aproximar la AMPLITUD pasando
de 10,5 a 11 y repetir el proceso.
(Esto se debe aplicar solo en el
caso de que suceda este tipo de
eventos)
LIMITES REALES
Límites Reales
Inferior Superior
27,5 38,0
37,7 48,5
48,9 59,0
59,1 69,5
69,3 80,0
79,3 90,5

11. Una vez logrado que el ultimo limite
superior sea igual a superior al valor
máximo del conjunto de datos, entramos a
contar cuando valores pertenecientes al
conjunto de datos están en cada uno de los
limites, por ejemplo: En el primer intervalo
(De 27,5 a 38,5) se encuentran los valores
28, 29, 36 y 38 para un total de 4 lo que
representa la frecuencia absoluta
individual. Repetimos el proceso para los
demás intervalos.
La suma de las frecuencias individuales
debe ser igual al total de datos, en este caso
a 25
Límites
reales
Frecuencia
absoluta (fi)
27,5-38,5 4
38,5-49,5 6
49,5-60,5 3
60,5-71,5 4
71,5-82,5 4
82,5-93,5 4

12. • La marca de clase (Xi) es el punto medio de cada intervalo de clase
𝑋𝑖 = Limite inferior de clase + Limite superior de clase
2
• La frecuencia relativa (fri) de un dato o de una clase se encuentra
dividiendo la
frecuencia de dicho dato (o de la clase) entre el total de datos.
𝑟𝑖
𝑓𝑖
𝑓 =
𝑛
• La frecuencia acumulada (Fi) de cualquier dato o clase, es la suma de la
frecuencia de ese mismo dato o clase con las frecuencias de todos los
demás datos o clases anteriores
𝐹𝑖 = 𝐹𝑖−1 + 𝑓𝑖
• La frecuencia relativa acumulada (Fri) de un dato o de una clase se
obtiene dividiendo la frecuencia acumulada del dato o de la clase por el
número total de datos.
𝑟𝑖
𝐹𝑖
𝐹 =
𝑛
Otros valores a
calcular para
completar nuestra
tabla de frecuencias
son:

13. Límites
reales Xi fi fr Fi Fr
27,5-38,5
(27,5+38,5)/2
= 33 4
4/25=0,12=
16% 4 16%
38,5-49,5 44 6 24% 3+6=9 16%+24%=40%
49,5-60,5 55 3 12% 10+3=13 40%+12%=52%
60,5-71,5 66 4 16% 13+4=17 52%+16%=68%
71,5-82,5 77 4 16% 17+4=21 68%+16%=84%
82,5-93,5 88 4 16% 21+4=25 84%+16%=100%
Obteniendo los
siguientes
resultados:

14. Clases Límites reales Xi fi
28 – 38 27,5-38,5 33 4
39 – 49 38,5-49,5 44 6
50 – 60 49,5-60,5 55 3
61- 71 60,5-71,5 66 4
72 – 82 71,5-82,5 77 4
83 – 93 82,5-93,5 88 4
Histograma:

15. Clases Gastos Xi fi Fi
28 – 38 27,5-38,5 33 4 4
39 – 49 38,5-49,5 44 6 10
50 – 60 49,5-60,5 55 3 13
61- 71 60,5-71,5 66 4 17
72 – 82 71,5-82,5 77 4 21
83 – 93 82,5-93,5 88 4 25

16. Actividad 1: Los datos que se muestran a continuación representan el
costo (en miles de pesos) de la energía eléctrica durante un determinado
mes del año 2006 para una muestra aleatoria de 50 apartamentos
en cierta ciudad importante.
128 144 168 109 167 141 149 206 175 123
153 197 127 82 96 171 202 178 147 102
135 191 137 129 158 108 119 183 151 114
111 148 213 130 165 157 185 90 116 172
143 187 166 139 149 95 163 150 154 130
a) Obtenga una tabla de frecuencias con 7 intervalos de clase.
b) Grafique el correspondiente histograma de frecuencias, el polígono de
frecuencias
c) ¿Alrededor de qué cantidad parece concentrarse el costo mensual de
energía eléctrica?