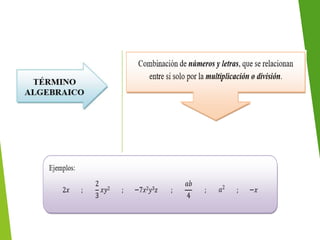
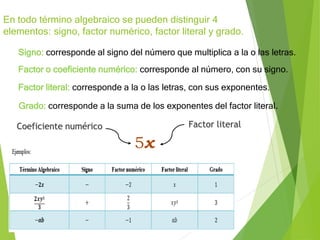
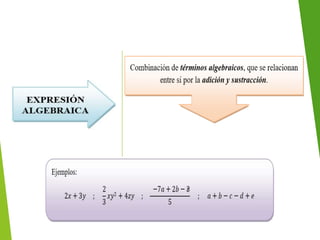
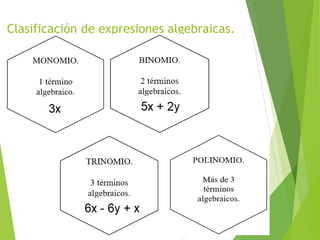
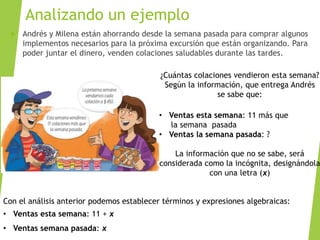
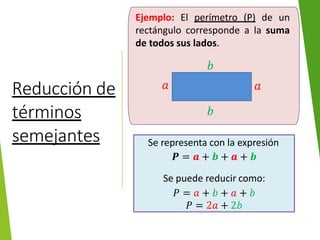
El documento explica los elementos de un término algebraico (signo, factor numérico, factor literal y grado) y cómo valorizar expresiones algebraicas asignándoles un valor numérico a las letras. También muestra ejemplos de cómo calcular el valor de expresiones algebraicas después de valorizar las letras con números conocidos.

1. TÉRMINOS Y
EXPRESIONES
ALGEBRAICAS
Profesor Esteban Vera
6° básico

3. En todo término algebraico se pueden distinguir 4
elementos: signo, factor numérico, factor literal y grado.
Signo: corresponde al signo del número que multiplica a la o las letras.
Grado: corresponde a la suma de los exponentes del factor literal.
Factor literal: corresponde a la o las letras, con sus exponentes.
Factor o coeficiente numérico: corresponde al número, con su signo.
5x
Factor literal
Coeficiente numérico

5. Clasificación de expresiones algebraicas.

6. VALORIZAR
EXPRESIONES
ALGEBRAICAS
Valorizar una
expresión algebraica
consiste en
asignarle un valor
numérico a la letra
(literal o incógnita)
para poder
desarrollar las
operaciones.

7. Analizando un ejemplo
 Andrés y Milena están ahorrando desde la semana pasada para comprar algunos
implementos necesarios para la próxima excursión que están organizando. Para
poder juntar el dinero, venden colaciones saludables durante las tardes.
¿Cuántas colaciones vendieron esta semana?
Según la información, que entrega Andrés
se sabe que:
• Ventas esta semana: 11 más que
la semana pasada
• Ventas la semana pasada: ?
La información que no se sabe, será
considerada como la incógnita, designándola
con una letra (x)
Con el análisis anterior podemos establecer términos y expresiones algebraicas:
• Ventas esta semana: 11 + x
• Ventas semana pasada: x

8. Valorizando…
 Si según el caso anterior, Milena le dice a Andrés que la cantidad
vendida la semana anterior es de 23 colaciones.
 Entonces, para saber cuántas colaciones se vendieron en esta semana
se debe valorizar la expresión que estableció Andrés.
Ventas esta semana: 11 + x
Valorizamos la expresión con x = 23 colaciones de la semana anterior.
11 + x
11 + 23
34
Por lo tanto, esta semana se han vendido 34
colaciones.

9. Ahora tú… en tu cuaderno.
 ¿Según el ejercicio anterior, cual es la expresión
algebraica que representa lo recaudado en la venta del
total de colaciones si se venden a x pesos?
Expresión: _________________
 Si se vende cada colación a $500. ¿Cuánto fue lo
recaudado?
Respuesta: _________________
• Ventas esta semana: 11 + x
• Ventas semana pasada: x

10. Más ejemplos…
 Determina el valor del área del rectángulo que se
muestra a continuación considerando para sus medidas
x = 5
 Valorizamos:
 Largo (base): 3x cm
3∙5
15 cm
 Ancho (alto): 2x cm
2∙5
10 cm
Recuerda que el área
se expresa en unidades
de medida al
cuadrado. (𝑢2
)
El área del rectángulo son 150𝑐𝑚2
Utilizando la fórmula para el cálculo del área del rectángulo
A = base ∙ altura
A = 15cm ∙ 10cm
A = 150𝑐𝑚2

11. REDUCCIÓN DE
EXPRESIONES
ALGEBRAICAS
(términos semejantes)
Profesor Esteban Vera
Profesora Franchesca Vallejos
7° básico

12. Reducción de
términos
semejantes
Si en una expresión algebraica hay
términos semejantes, sus
coeficientes numéricos se pueden
sumar o restar. Después de realizar
estas operaciones, la expresión
algebraica obtenida tiene menos
términos, por lo que este proceso
es conocido como reducción de
términos semejantes.
Cuando se reducen los términos
semejantes, se suman o se restan
sus coeficientes numéricos y se
conserva el factor literal.

13. Reducción de
términos
semejantes
Ejemplo: El perímetro (P) de un
rectángulo corresponde a la suma
de todos sus lados.
𝑎 𝑎
𝑏
𝑏
Se representa con la expresión
𝑷 = 𝒂 + 𝒃 + 𝒂 + 𝒃
Se puede reducir como:
𝑃 = 𝑎 + 𝑏 + 𝑎 + 𝑏
𝑃 = 2𝑎 + 2𝑏

14. RECUERDA:
Cuando se reducen
lostérminos
semejantes, se
suman o se
restan sus coeficientes
numéricos y se
conserva el factor
literal.
Ejemplo 1
𝟒𝒙 + 𝟏𝟐𝒙𝒚 + 𝟑𝒙 + 𝟏𝟔𝒙𝒚 + 𝒙
𝟒𝒙 + 𝟏𝟐𝒙𝒚 + 𝟑𝒙 + 𝟏𝟔𝒙𝒚 + 𝒙
(𝟒𝒙 + 𝟑𝒙 + 𝒙) + (𝟏𝟐𝒙𝒚 + 𝟏𝟔𝒙𝒚)
𝟖𝒙 + 𝟐𝟖𝒙𝒚
Agrupas los números con
X y los sumas, cuando
una letra está sola como
la X vale 1 en este caso
4x +3x + x =8x
En el caso de los números con XY
haces lo mismo, sumas
12xy + 16xy = 28xy

15. RECUERDA:
Cuando se reducen
lostérminos
semejantes, se
suman o se
restan sus coeficientes
numéricos y se
conserva el factor
literal.
Ejemplo 2
𝟏𝟒𝒙𝒚 + 𝟓𝒙 − 𝟐𝒙𝒚 − 𝟑𝒙
𝟏𝟒𝒙𝒚 + 𝟓𝒙 − 𝟐𝒙𝒚 − 𝟑𝒙
(𝟏𝟒𝒙𝒚 − 𝟐𝒙𝒚) + (𝟓𝒙 − 𝟑𝒙)
𝟏𝟐𝒙𝒚 + 𝟐𝒙