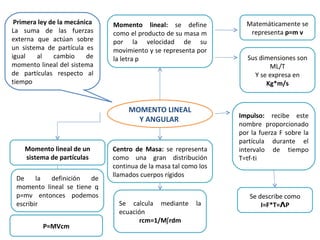
Este documento trata sobre el momento lineal y angular en física. Define el momento lineal como el producto de la masa y la velocidad de una partícula, y el momento angular como el producto vectorial entre el vector posición de una partícula y su momento lineal. Explica que la primera ley de la mecánica establece que la suma de las fuerzas externas sobre un sistema es igual al cambio en su momento lineal, mientras que la segunda ley indica que el cambio en el momento angular de un sistema es igual al momento de torsión externo sobre él. También

1. Instituto Universitario Politécnico
Santiago Mariño
MOMENTO LINEAL Y
ANGULAR
Materia: Física I Alumno:
Prof.: Malek El Masri TSU Martín Vegas
18858312
Escuela 46

2. Primera ley de la mecánica Momento lineal: se define Matemáticamente se
La suma de las fuerzas como el producto de su masa m representa p=m v
externa que actúan sobre por la velocidad de su
un sistema de partícula es movimiento y se representa por
igual al cambio de la letra p Sus dimensiones son
momento lineal del sistema ML/T
de partículas respecto al Y se expresa en
tiempo Kg*m/s
MOMENTO LINEAL
Impulso: recibe este
Y ANGULAR
nombre proporcionado
por la fuerza F sobre la
partícula durante el
Momento lineal de un Centro de Masa: se representa intervalo de tiempo
sistema de partículas como una gran distribución T=tf-ti
continua de la masa tal como los
llamados cuerpos rígidos
De la definición de
momento lineal se tiene q
p=mv entonces podemos Se describe como
escribir Se calcula mediante la I=F*T=ɅP
ecuación
rcm=1/Mʃ rdm
P=MVcm

3. Matemáticamente se
Momento Angular: se define representa
Momento de inercia es la como el producto vectorial del L =r*p o
resistencia de un objeto a vector posición instantánea r de L=mr*v
los cambios en su estado de la partícula y su momento lineal
movimiento rotacional. p=mv
Las unidades del
la inercia rotacional momento angular son
depende de la distribución Kg*m2/s
de la masa.
I=mr2
Donde m es la masa de la MOMENTO LINEAL La magnitud del
partícula y r es su distancia Y ANGULAR momento angular esta
al eje de rotación. El dado por
momento de inercia I es L=mrv senφ
una cantidad escalar, y sus
unidades en el sistema Inercia: es la propiedad que Donde φ es el angulo
internacional (SI) son tienen los cuerpos de entre r y p
Kg.m2. permanecer en su estado de
reposo o movimiento, O también L=mr2w
mientras no se aplique sobre Donde V=rw es la
ellos alguna fuerza, o la velocidad angular de
Vectorialmente el momento
resistencia que opone la rotación.
angular se puede expresar por
materia al modificar su estado
L=lw
de reposo o movimiento

4. El momento de
Momento de torsión: producido por la fuerza torsión y el momento
F, está dado por τ=Fb. Donde b es el brazo de angular deben
fuerza. De la figura se tiene b=rsenθ Entonces evaluarse respecto al
τ =rF senθ En forma vectorial, el momento de mismo origen de un
torsión es expresado por τ =r×F sistema de referencia
inercial
MOMENTO LINEAL
PRINCIPIO DE CONSERVACIÓN
DEL MOMENTO ANGULAR Y ANGULAR
nos indica que si “el
momento de torsión neto 2a ley de la Mecánica: la cual nos
sobre un sistema de dice que “el momento de torsión
partículas es cero, el externo que actúa sobre un sistema
momento angular se de partículas es igual a la razón de
mantiene constante”. Esto cambio respecto al tiempo del
constituye el Principio de momento angular total del
Conservación del sistema”.
Momento Angular.