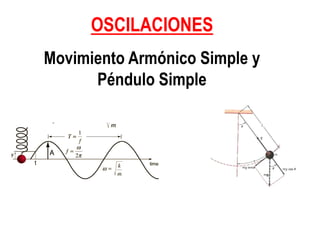
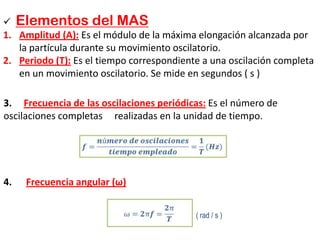
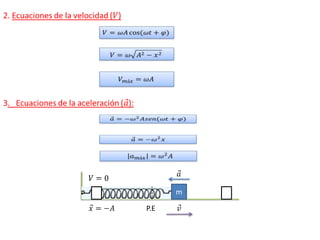
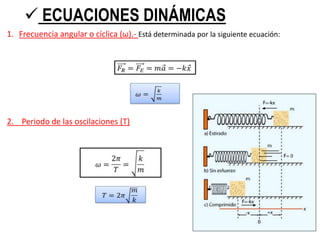
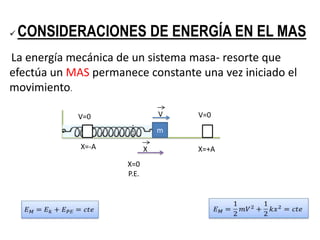
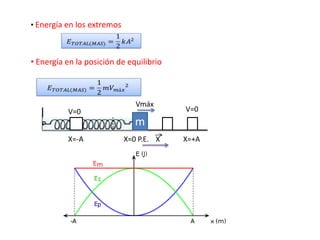
Este documento describe el movimiento armónico simple y el péndulo simple. Explica conceptos como amplitud, periodo, frecuencia, ecuaciones cinemáticas y dinámicas para el movimiento armónico simple. También cubre consideraciones de energía, leyes del péndulo como la del isocronismo y de las longitudes, y presenta ejemplos de problemas sobre péndulos.

1. OSCILACIONES
Movimiento Armónico Simple y
Péndulo Simple

2. Conceptos básicos
• Movimiento oscilatorio: Es todo
movimiento o cambio de estado físico que
se repite en el tiempo, según su naturaleza
física de las oscilaciones pueden ser:
mecánicas, electromagnéticas, atómicas, etc
.
• Movimiento periódico: Es aquel cuyos
valores variables de sus magnitudes físicas
se repiten en cierto intervalo de tiempo
constante llamado periodo (T)
• Movimiento Armónico Simple (MAS): Es
un movimiento oscilatorio y periódico que
presenta una trayectoria recta.

3.  Elementos del MAS
1. Amplitud (A): Es el módulo de la máxima elongación alcanzada por
la partícula durante su movimiento oscilatorio.
2. Periodo (T): Es el tiempo correspondiente a una oscilación completa
en un movimiento oscilatorio. Se mide en segundos ( s )
3. Frecuencia de las oscilaciones periódicas: Es el número de
oscilaciones completas realizadas en la unidad de tiempo.
4. Frecuencia angular (ω)
( rad / s )

4. ECUACIONES CINEMÁTICAS
1. Ecuación de la posición o elongación (x):
A
x
m
V=0
X

5. mm
P.E

6. 1. Frecuencia angular o cíclica (ω).- Está determinada por la siguiente ecuación:
2. Periodo de las oscilaciones (T)
 ECUACIONES DINÁMICAS

7. 3. Frecuencia de las oscilaciones (f)
Nota:
La frecuencia angular (ω), el periodo (T) y la
frecuencia de las oscilaciones(f) solo dependen
de las características físicas del
resorte(constante de electricidad) y de la masa
del cuerpo oscilante y no depende de la
amplitud ni de la forma como se inicia el
movimiento.

8.  CONSIDERACIONES DE ENERGÍA EN EL MAS
La energía mecánica de un sistema masa- resorte que
efectúa un MAS permanece constante una vez iniciado el
movimiento.
m
X=0
P.E.
V=0 V=0V
X=-A X X=+A

9. • Energía en los extremos
• Energía en la posición de equilibrio
m
V=0 V=0
X=0 P.E.X=-A
Vmáx
X X=+A

13. • Un relojero fue el primero en despertar el
interés del físico y astrónomo italiano Galileo
por la mecánica .Dos características lo
fascinaron: que el periodo parecía
independiente de la amplitud de la
oscilación, y que también parecía
independiente de la masa de la lenteja.

14. • Por medio de mediciones cuidadosas Galileo
encontró que el péndulo dependía de la
longitud de la cuerda L .Esta dependencia se
ha utilizado durante siglos para ajustar los
relojes de péndulo.

15. • El péndulo es un sistema físico
constituido de un hilo
inelástico fijo por un extremo,
sosteniendo por el otro a una
lenteja ,que al oscilar lo hace
con M.A.S.

16. Longitud pendular (L)
Masa pendular (m)
Oscilación (BOA+AOB)
Periodo (T= t(BOA) + t(AOB) )
Amplitud angular (
Amplitud lineal (A)
α< 10 )

17. • LEY DEL ISOCRONISMO:
• Establece que el movimiento pendular tiene un periodo independiente de la
amplitud, siempre que este no exceda los 10°
•LEY DE LAS ACELERACIONES DE LAS
GRAVEDADES:
La aceleración de la gravedad ejerce una acción primordial que influye en el
tiempo de oscilación del péndulo.

18. • LEY DE LONGITUDES:
A menor longitud menor
periodo de oscilación y a
mayor longitud mayor periodo
de oscilación.
En símbolos:
T1 y T2: tiempos de oscilación;
l1 y l2 : longitudes.
Para nuestro caso es:
T1= 1 oscilación y l1= 1dm
T2 = 2 oscilaciones y l2 =4 dm.

19. • LEY DE MASAS:
Las tres masas de la figura son distintas entre si, pero el
periodo (T) de oscilación es el mismo. (T1=T2=T3)
Los tiempos de oscilación
de varios péndulos de igual
longitud son
independientes de sus
masas y de su naturaleza.

20. FÓRMULA DEL PERIODO
• El periodo de un péndulo es directamente proporcional a la
longitud pendular e inversamente con la aceleración de la
gravedad. Su valor esta dado por:
• Por tanto la frecuencia será:

21. PROBLEMA 1:
• Un péndulo oscila con un péndulo de 2s y una longitud
de 9m. ¿Qué longitud deberá tener para que su periodo
se duplique?
2T1 = T2 T1=2s
(T1 / 2 T1 )2 = 3/ L2
L2 = 36m

22. PROBLEMA 2:
• Un péndulo de 40 oscilaciones en 5s, y un segundo da 60
oscilaciones en 6s. ¿En que relación se encontrara la longitud
del primero respecto de la del segundo?
f1 = 8 osc/s f2 = 10 osc/s
f1 / f2 = 4/5
(4/5)2 = L1 / L2
L1 / L2 = 16/25

23. PROBLEMA 3:
• Un péndulo de 0,8 m oscila armónicamente con una
amplitud de 8cm. ¿Cuál es la máxima velocidad y
aceleración que posee la masa pendular durante su
movimiento oscilatorio?