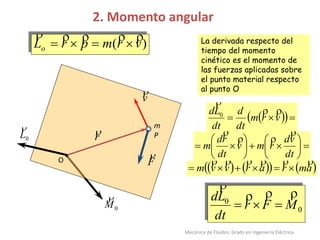
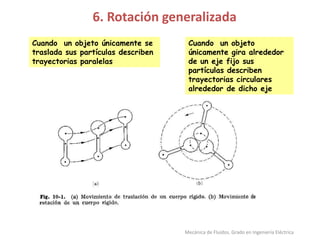
Este documento presenta los conceptos fundamentales de la teoría de momentos y rotación en mecánica de fluidos. Explica el momento de un vector, momento angular, momento de inercia, teorema de Steiner, momento de las fuerzas externas, rotación de un sólido rígido, conservación del momento angular y la segunda ley de Newton aplicada a la dinámica de rotación. Finaliza con una tabla resumen de las analogías entre la dinámica de traslación y rotación.

1. UNIVERSITAT POLITÈCNICA DE VALÈNCIA
CURSO: MECÁNICA DE FLUIDOS
TEMA 3. Conceptos previos:
Teoría de Momentos y Rotación

2. 1. Momento de un vector respecto a un punto
2. Momento angular o cinético
2.1 Ecuación fundamental de la dinámica de rotación
3. Momento de inercia
4. Teorema de Steiner
5. Momento de las fuerzas exteriores
6. Rotación de un sólido rígido alrededor de un eje
7. Conservación del momento angular
7.1. Segunda ley de Newton en la dinámica de rotación
8. Tabla resumen
Índice
Mecánica de Fluidos. Grado en Ingeniería Eléctrica

3. v

Momento de un vector
respecto a un punto O
vOPM



M

O
P
   


zyx
zyx
zyxzyx
bbb
aaa
kji
kbjbibkajaiaba


     kbabajbabaibaba xyyxzxxzyzzy


Mecánica de Fluidos. Grado en Ingeniería Eléctrica
1. Momento de un vector

4. 2. Momento angular
Mecánica de Fluidos. Grado en Ingeniería Eléctrica
)( vrmprLo


Momento angular o
cinético de un punto
material respecto de un
punto O es el momento
de la cantidad de
movimiento respecto a
dicho punto O
r

v

m
P
O
Propiedades de 0L
r
0L


5. 2. Momento angular
   vrm
dt
d
dt
Ld 

0
La derivada respecto del
tiempo del momento
cinético es el momento de
las fuerzas aplicadas sobre
el punto material respecto
al punto O
)( vrmprLo


0
0
MFr
dt
Ld 















dt
vd
rmv
dt
rd
m



      amrarvvm


0M

v

O
r

m
P0L

F

Mecánica de Fluidos. Grado en Ingeniería Eléctrica

6. 3. Momento de Inercia
El momento de inercia I en dinámica de rotación, es el análogo a
la masa en dinámica de traslación
Para un sistema de discreto de n partículas:
Para un sistema de partículas continuo:
2
1
n
i i
i
I m r


2
I r dm
Mecánica de Fluidos. Grado en Ingeniería Eléctrica

7. 3. Momento de Inercia
l=dm/dl
dm=l·dl
s=dm/ds
dm=s·ds
=dm/dV
dm=·dV
Densidad lineal l
Densidad superficial s
Densidad volumétrica 
Mecánica de Fluidos. Grado en Ingeniería Eléctrica

8. 3. Momento de Inercia
Momentos de inercia
de cuerpos rígidos
homogéneos con
diferentes formas
geométricas
Mecánica de Fluidos. Grado en Ingeniería Eléctrica

9. 4. Teorema de Steiner
Este teorema permite calcular
el momento de inercia de un
sólido respecto a un eje
paralelo a uno que pase por el
centro de masas (CM) de dicho
sólido
Matemáticamente
2
·E CMI I M h 
El momento de inercia IE respecto a un eje E paralelo al eje que pasa
por el centro de masas es igual al momento de inercia respecto al
centro de masas ICM más el producto de la masa M por la distancia de
separación entre ambos ejes al cuadrado
E
Copyright (c) 2000 by W. H. Freeman and Company and Worth
Publishers (Freeman/Worth).
Tipler Physics textbook
Mecánica de Fluidos. Grado en Ingeniería Eléctrica

10. 5. Momento de las fuerzas exteriores:
caso particular de la presión
   

 dALsendAyLAy
sen
D
M Goo
2

Teorema de Varignon: En un sistema de vectores deslizantes paralelos el
momento Resultante de las fuerzas es igual al momento de la Resultante
G
G
G
G
G
G
G
oo
Ay
I
seny
Ay
A
sen
y
I
sen
Ay
I
senD
























2
2
2
2
2
Mecánica de Fluidos. Grado en Ingeniería Eléctrica
R
D
G
y
dA
G
yG

o
L
Teorema de SteinerR=resultante =pGA =yGA
dF
dF=ydA

11. 6. Rotación generalizada
El movimiento más general de un sólido rígido en el espacio se puede
analizar estudiando dos tipos de movimiento simultáneos:
a) Traslación del centro de masas (CM) del sólido
b) Rotación del sólido alrededor de un eje que pasa por el centro de
masas
Mecánica de Fluidos. Grado en Ingeniería Eléctrica

12. 6. Rotación generalizada
Cuando un objeto únicamente se
traslada sus partículas describen
trayectorias paralelas
Cuando un objeto
únicamente gira alrededor
de un eje fijo sus
partículas describen
trayectorias circulares
alrededor de dicho eje
Mecánica de Fluidos. Grado en Ingeniería Eléctrica

13. 6. Rotación generalizada
En dinámica de traslación se
cumple que p mv
Al ser el momento cinético L el
análogo a p, en rotación se
cumplirá que
L I
Traslación Rotación
m (masa) I (momento de inercia)
v (velocidad lineal) ω (velocidad angular)
p (momento lineal o
cantidad de movimiento)
L (momento angular o
cinético)
Copyright (c) 2000 by W. H. Freeman and
Company and Worth Publishers
(Freeman/Worth).
Tipler Physics textbook
La velocidad angular ω es un
vector dirigido a lo largo del
eje de giro
Mecánica de Fluidos. Grado en Ingeniería Eléctrica

14. 7. Conservación del Momento angular
0
externo
dL
M
dt

r
r
Ecuación fundamental en la dinámica de rotación para un sistema de
partículas o sólido rígido
Si el sistema está aislado o Mexterno = 0 se cumple que
0
00 constanteexterno
dL
M L
dt
   
r
r r
Por tanto, en un sistema aislado el momento angular o cinético
permanece constante (no varía con el tiempo)
inicial finalL L
r r
Mecánica de Fluidos. Grado en Ingeniería Eléctrica

15. 7.1. Segunda Ley de Newton en rotación
En dinámica de traslación se tiene que
F ma
r r
En dinámica de rotación se ha de cumplir que
M I
r r
Traslación Rotación
m (masa) I (momento de inercia)
v (velocidad lineal) ω (velocidad angular)
a (aceleración lineal) α (aceleración angular)
p (momento lineal o cantidad de
movimiento)
L (momento angular o cinético)
F (fuerza) M (momento de una fuerza)
Mecánica de Fluidos. Grado en Ingeniería Eléctrica

16. 8. Tabla resumen
Traslación Rotación
x (desplazamiento lineal) θ ( desplazamiento angular)
v (velocidad lineal) ω (velocidad angular)
a (aceleración lineal) α (aceleración angular)
m (masa) I (momento de inercia)
p = mv (momento lineal o cantidad de
movimiento)
L = I ω (momento angular o cinético)
F (fuerza) M (momento de una fuerza)
F = dp/dt
F = ma (2ª ley de Newton)
M = dL/dt
M = I α (2ª ley de Newton)
pincial= pfinal (conservación de la
cantidad de movimiento)
Lincial= Lfinal (conservación del
momento angular o cinético)
Mecánica de Fluidos. Grado en Ingeniería Eléctrica