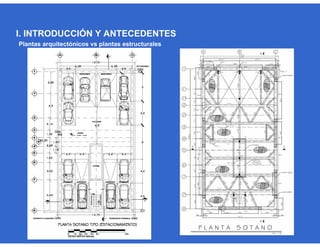
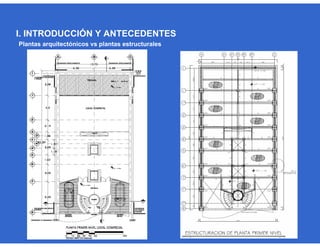
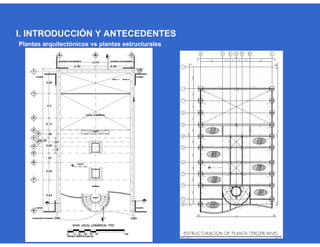
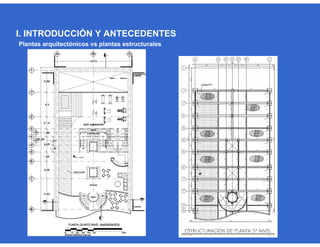
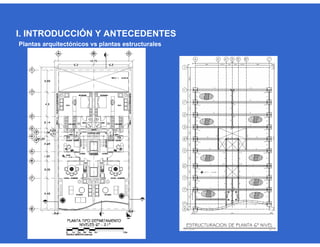
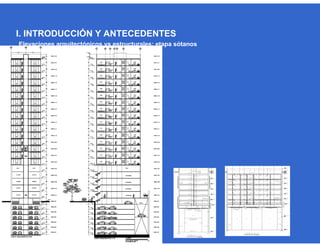
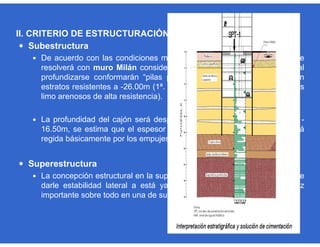
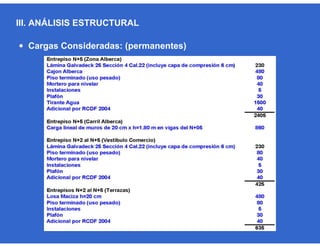
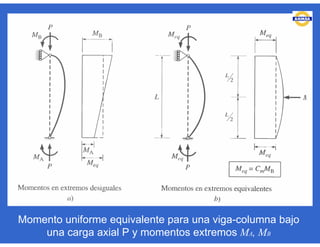
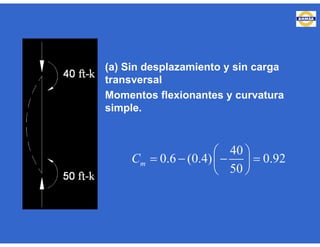
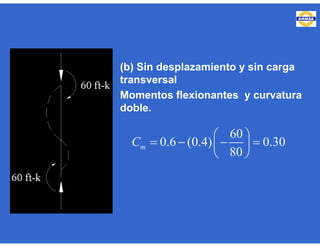
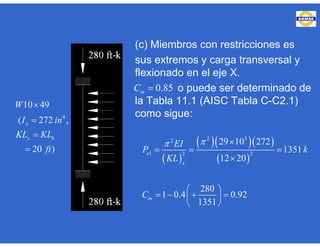
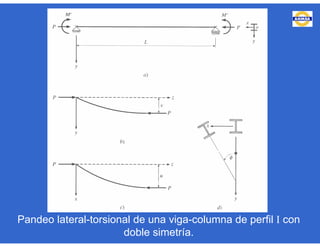
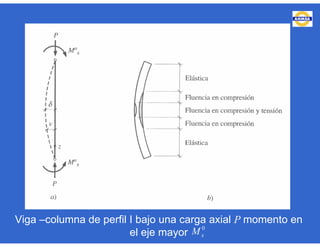
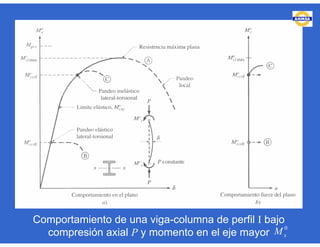
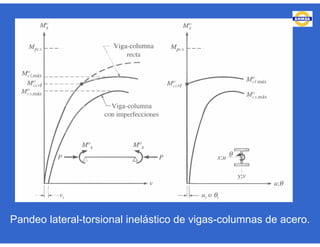
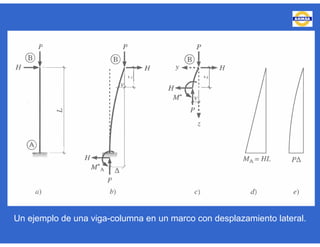
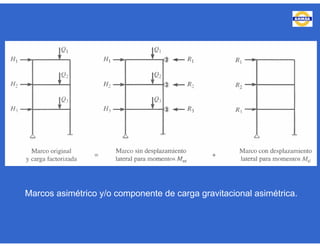
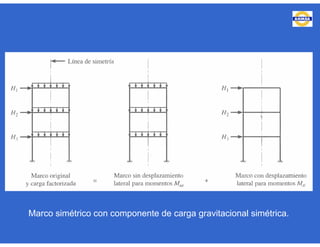
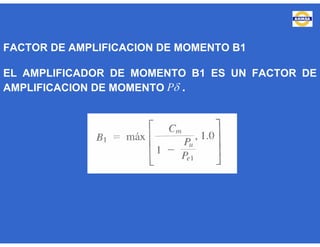
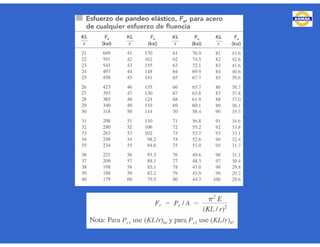
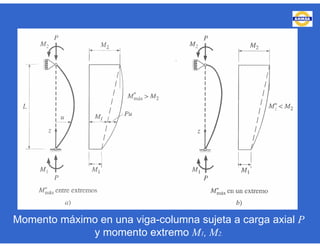
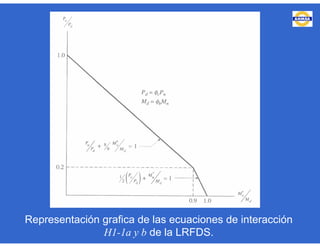
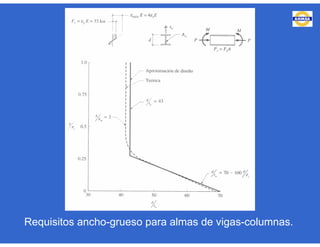
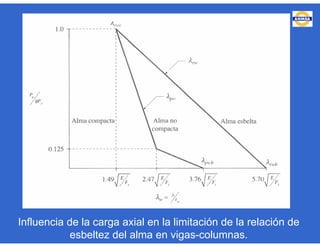
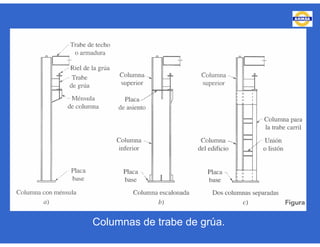
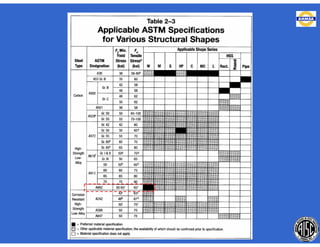
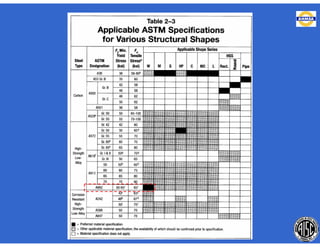
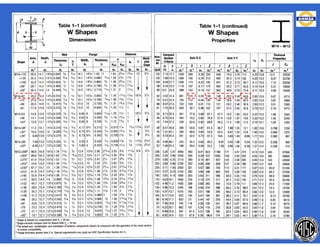
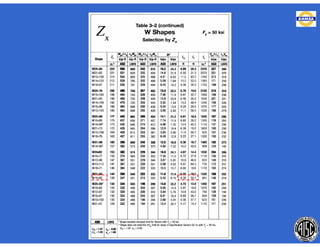
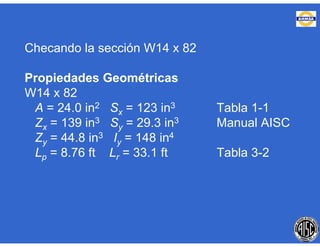
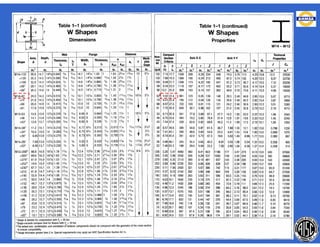
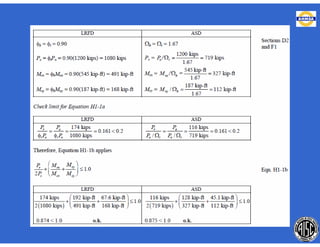
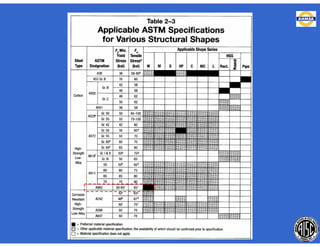
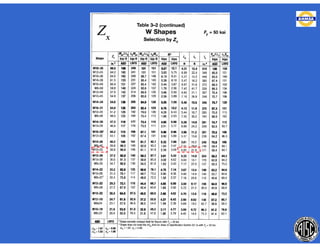
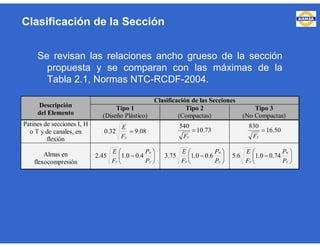
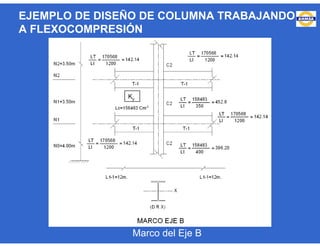
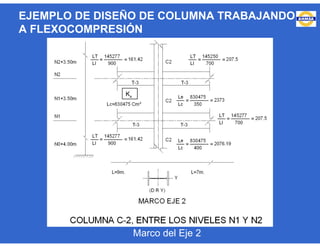
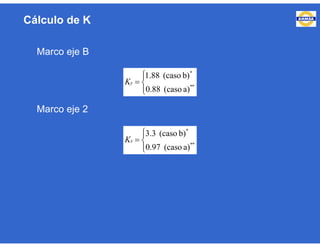
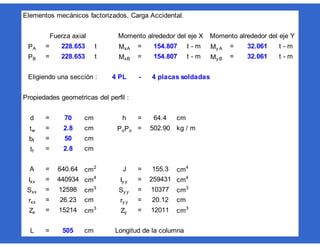
Este documento trata sobre el diseño, fabricación y montaje de estructuras de acero para edificios de acuerdo con las especificaciones AISC 2005. Explica conceptos como vigas-columnas, parámetros que afectan el comportamiento de columnas, miembros bajo fuerzas combinadas, resistencia a secciones sujetas a cargas combinadas, momentos de segundo orden en vigas-columnas, pandeo elástico y pandeo lateral-torsional de vigas-columnas. También incluye ejemplos de cálculo de resistencia de vigas-





















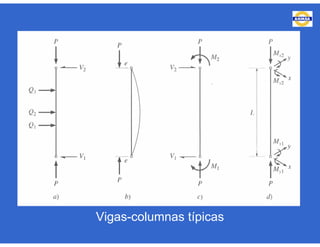
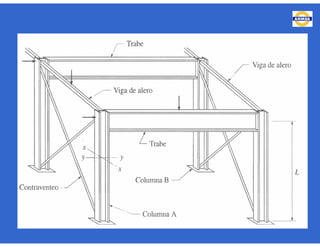
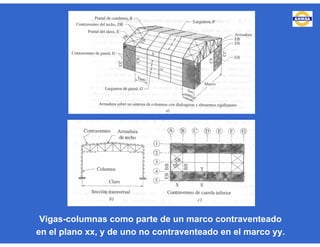


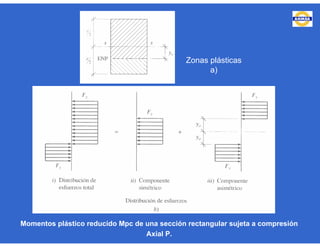









































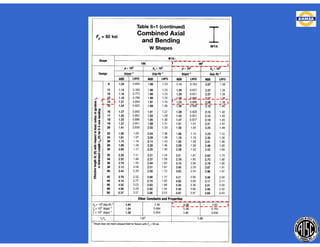
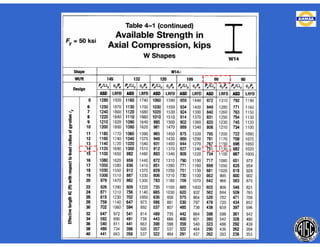




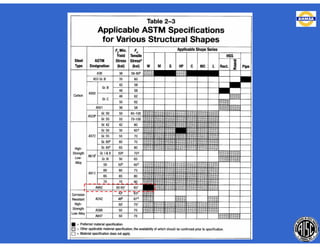
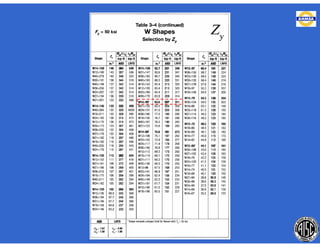
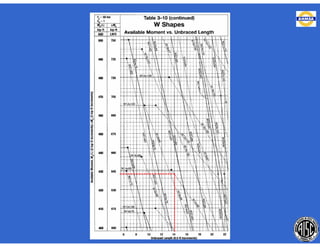
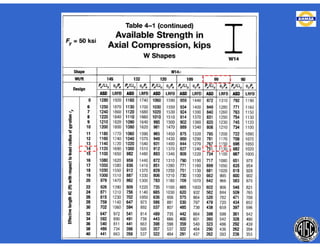




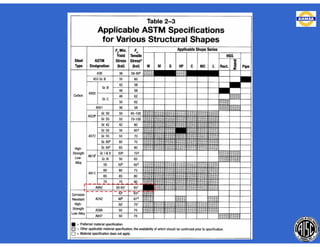

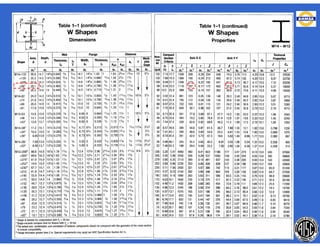





























































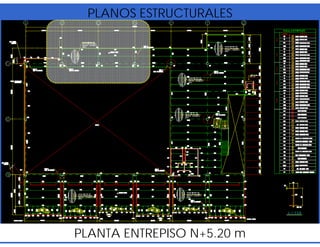
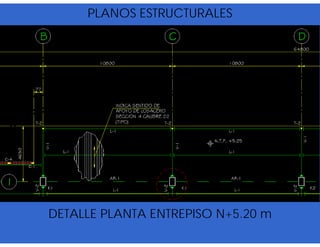
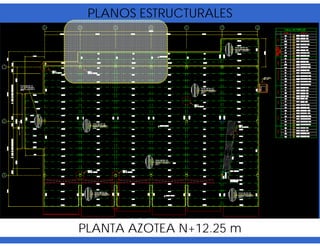
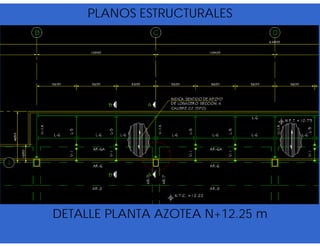

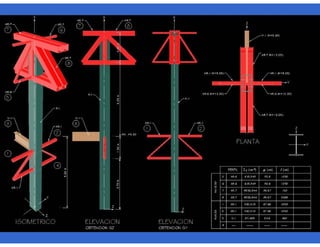
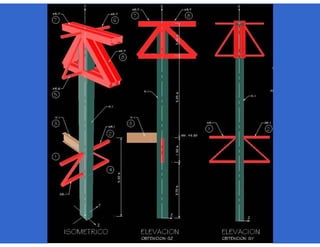









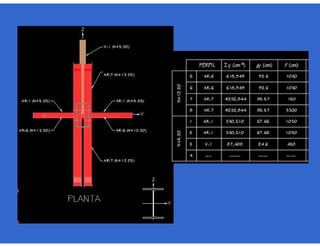
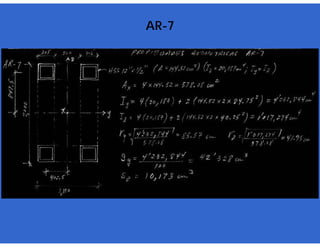

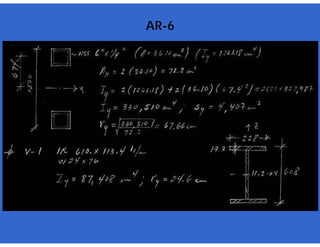




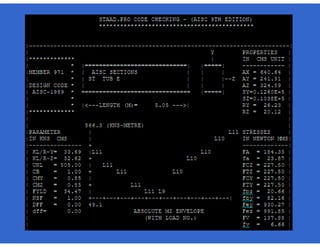
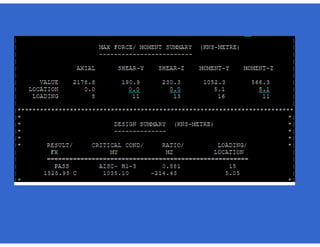




![- Resistencia de diseño a flexión.
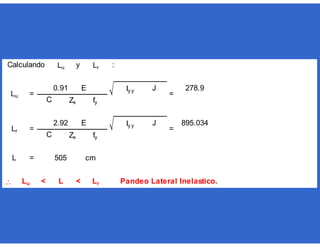
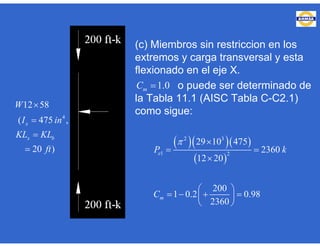
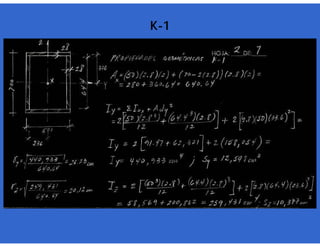
Calculando Ca
=
Calculando y
= + = +
= =
=
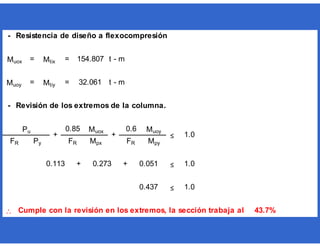
Calculando Mu
= * * 2
*
= t - m
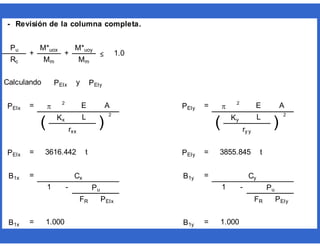
Ca 0 cm6
Mu 499.271
+ (
) Ca
]L
Mu E
Iy y [ J
C L 2.6
Cx 1.00 Cy 1.00
C 1.00
Cy 0.6 0.4 M1
M2 M2
Cx Cy
Cx 0.6 0.4 M1](https://image.slidesharecdn.com/flexocompresion-muycompleto-180224145919/85/Flexocompresion-muy-completo-223-320.jpg)