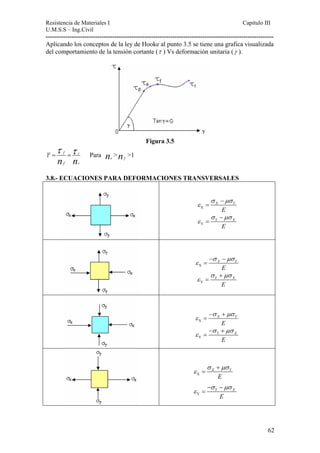
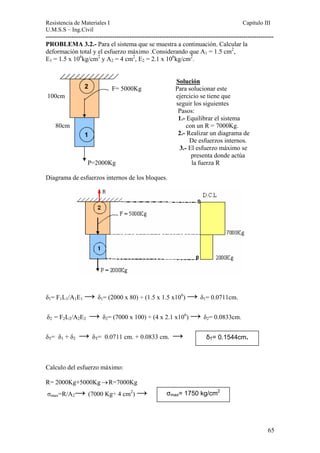
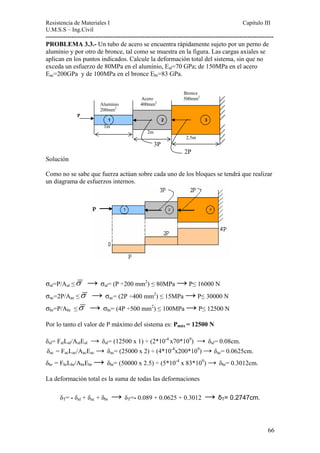
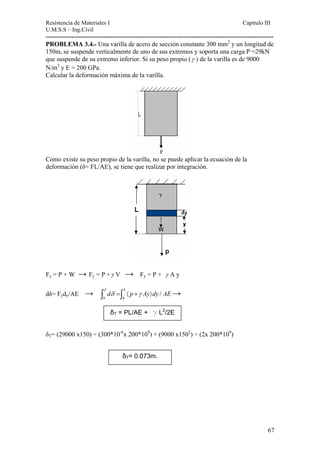
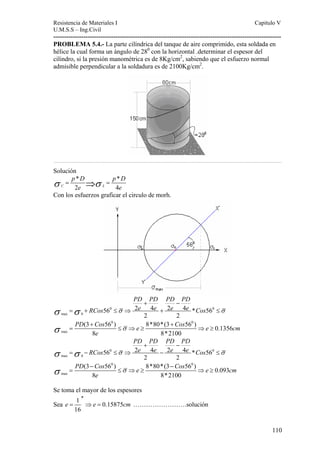
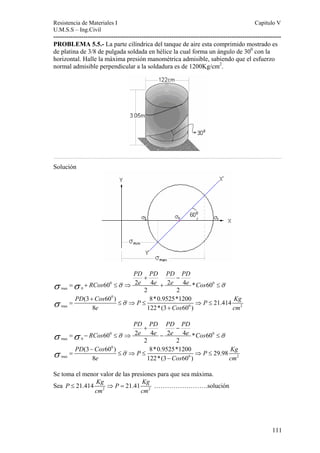
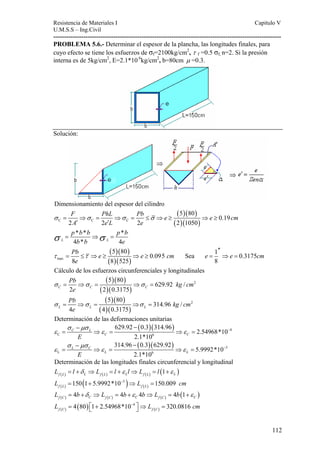
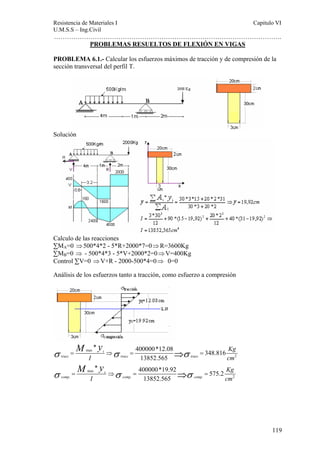
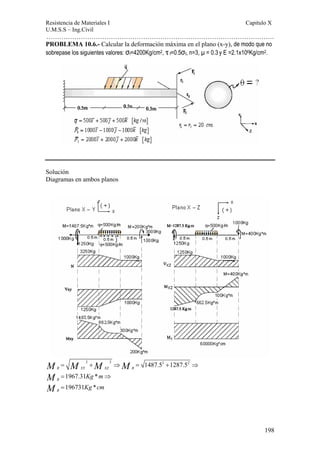
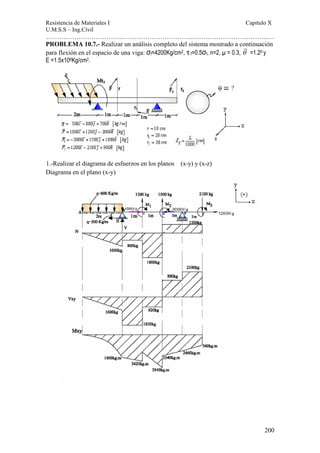
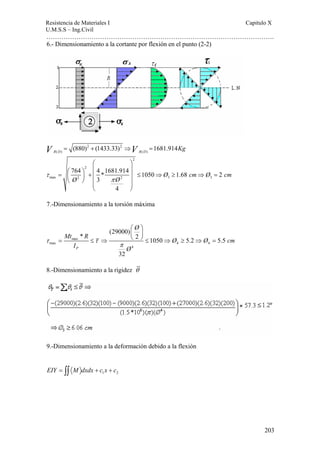
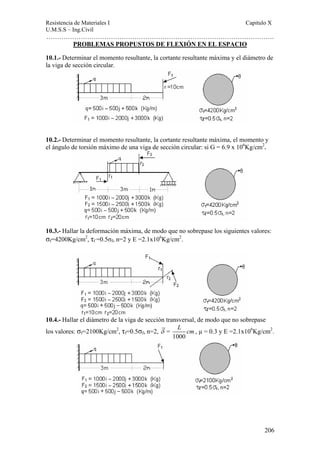
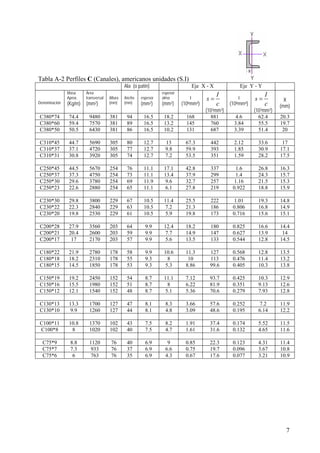
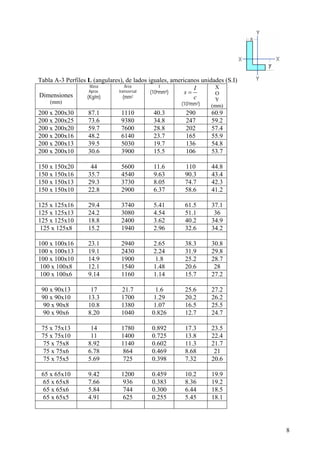
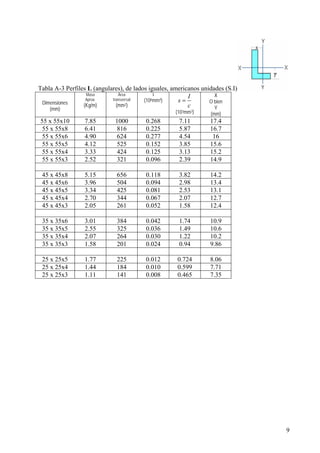
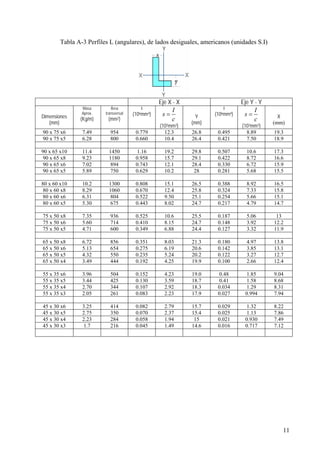
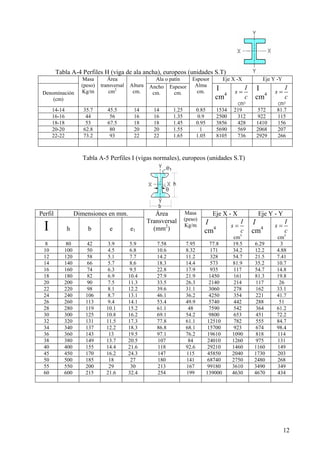
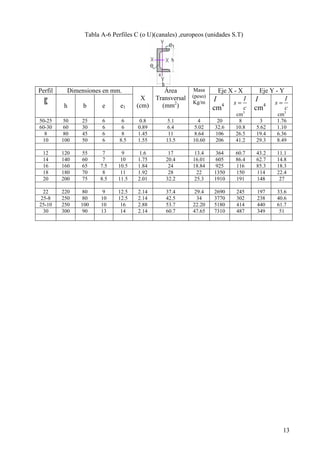
Este documento presenta un material de apoyo didáctico para la asignatura de Resistencia de Materiales I de la carrera de Ingeniería Civil de la Universidad Mayor de San Simón en Cochabamba, Bolivia. El documento está estructurado en dos partes principales que cubren conceptos básicos y capítulos sobre diferentes tipos de tensiones y su aplicación a elementos como vigas y cilindros. Incluye objetivos, contenido teórico, problemas resueltos y propuestos para cada capítulo, así como tablas de referencia sobre perfiles e