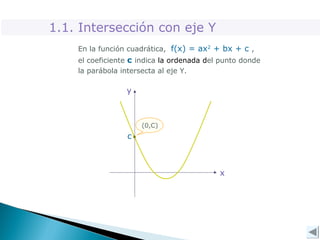
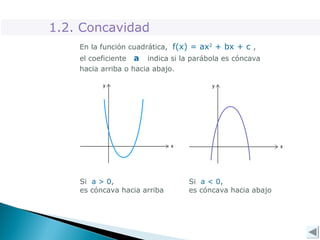
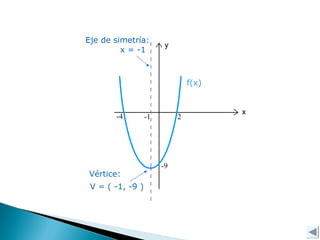
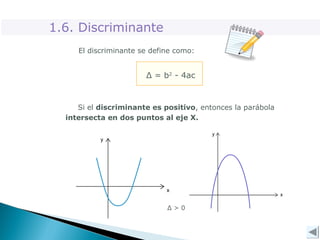
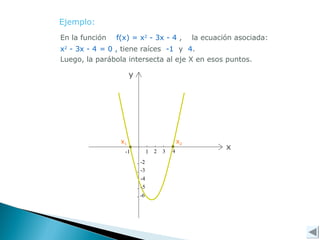
Este documento explica conceptos clave de las funciones cuadráticas y ecuaciones de segundo grado. Explica que una función cuadrática tiene la forma f(x)=ax^2 + bx + c y describe cómo los coeficientes a, b y c determinan la intersección con los ejes, la concavidad y el vértice. También cubre cómo resolver ecuaciones de segundo grado usando la fórmula de las raíces y el discriminante, el cual indica si las raíces son reales o complejas.

1. Profesora: MeryProfesora: Mery
MartínezMartínez

2. Contenidos
1.Función cuadrática
2.Ecuación de 2º grado
1.1 Intersección con el eje Y
1.2 Concavidad
1.3 Eje de simetría y vértice
2.1 Raíces de una ecuación cuadrática
2.2 Propiedades de las raíces
2.3 Discriminante
1.4 Discriminante

3. 1. Función Cuadrática
Es de la forma:
f(x) = ax2
+ bx + c
Ejemplos:
y su gráfica es una parábola.
a) Si f(x) = 2x2
+ 3x + 1
b) Si f(x) = 4x2
- 5x - 2
a = 2, b = 3 y c = 1
a = 4, b = -5 y c = -2
⇒
⇒
con a =0; a,b,c ∈ IR

4. 1.1. Intersección con eje Y
En la función cuadrática, f(x) = ax2
+ bx + c ,
el coeficiente c indica la ordenada del punto donde
la parábola intersecta al eje Y.
x
y
x
y
c
(0,C)

5. 1.2. Concavidad
En la función cuadrática, f(x) = ax2
+ bx + c ,
el coeficiente a indica si la parábola es cóncava
hacia arriba o hacia abajo.
Si a > 0,
es cóncava hacia arriba
Si a < 0,
es cóncava hacia abajo

6. Si f(x) = ax2
+ bx + c , entonces:
b) Su vértice es:
a) Su eje de simetría es:
2a 2a
V =
-b , f -b
4a
-b , 4ac – b2
2a
V =
-b
2a
x =

7. f(x)
V = ( -1, -9 )
x = -1
Eje de simetría:
Vértice:

8. El discriminante se define como:
Δ = b2
- 4ac
Si el discriminante es positivo, entonces la parábola
intersecta en dos puntos al eje X.
Δ > 0
1.6. Discriminante

9. x2
x1
2. Ecuación de segundo grado
Una ecuación cuadrática o de segundo grado es
de la forma:
ax2
+ bx + c = 0, con a ≠ 0
Toda ecuación de segundo grado tiene 2 soluciones o
raíces. Si éstas son reales, corresponden a los puntos
de intersección de la parábola f(x) = ax2
+ bx + c
con el eje X.

10. x2
x
y
x1
Ejemplo:
En la función f(x) = x2
- 3x - 4 , la ecuación asociada:
x2
- 3x - 4 = 0 , tiene raíces -1 y 4.
Luego, la parábola intersecta al eje X en esos puntos.

11. 2.1. Raíces de una ecuación de 2° grado
Fórmula para determinar las soluciones (raíces)
de una ecuación de segundo grado:
- b ± b2
– 4ac
2a
x =
Ejemplo:
Determinar las raíces de la ecuación: x2
- 3x - 4 = 0
-(-3) ± (-3)2
– 4·1(- 4)
2
x =
3 ± 9 + 16
2
x =

12. 3 ± 25
2
x =
2
x = 3 ± 5
2
x = 8
2
x = -2
x1 = 4 x2 = -1
También se puede obtener las raíces de la ecuación
factorizando como producto de binomios:
x2
- 3x - 4 = 0
(x - 4)(x + 1) = 0
(x - 4)= 0 ó (x + 1)= 0
x1 = 4 x2 = -1
⇒

13. 2.2. Propiedades de las raíces
Si x1 y x2 son las raíces de una ecuación de segundo
grado de la forma ax2
+ bx + c = 0, entonces:
-b
a
x1 + x2 =
c
a
x1 · x2 =
Δ
a
x1 - x2 = ±
1)
2)
3)
Dadas las raíces o soluciones de una ecuación de segundo
grado, se puede determinar la ecuación asociada a ellas.
a(x – x1)(x – x2) = 0

14. En una ecuación de segundo grado, el discriminante
Δ = b2
- 4ac
a) Si el discriminante es positivo, entonces la ecuación
cuadrática tiene dos soluciones reales x1, x2 y distintas.
La parábola intersecta
en dos puntos al eje X.
Δ > 0
2.3. Discriminante
permite conocer la naturaleza de las raíces.
x1, x2 son reales y
x1 ≠ x2
x2
x1