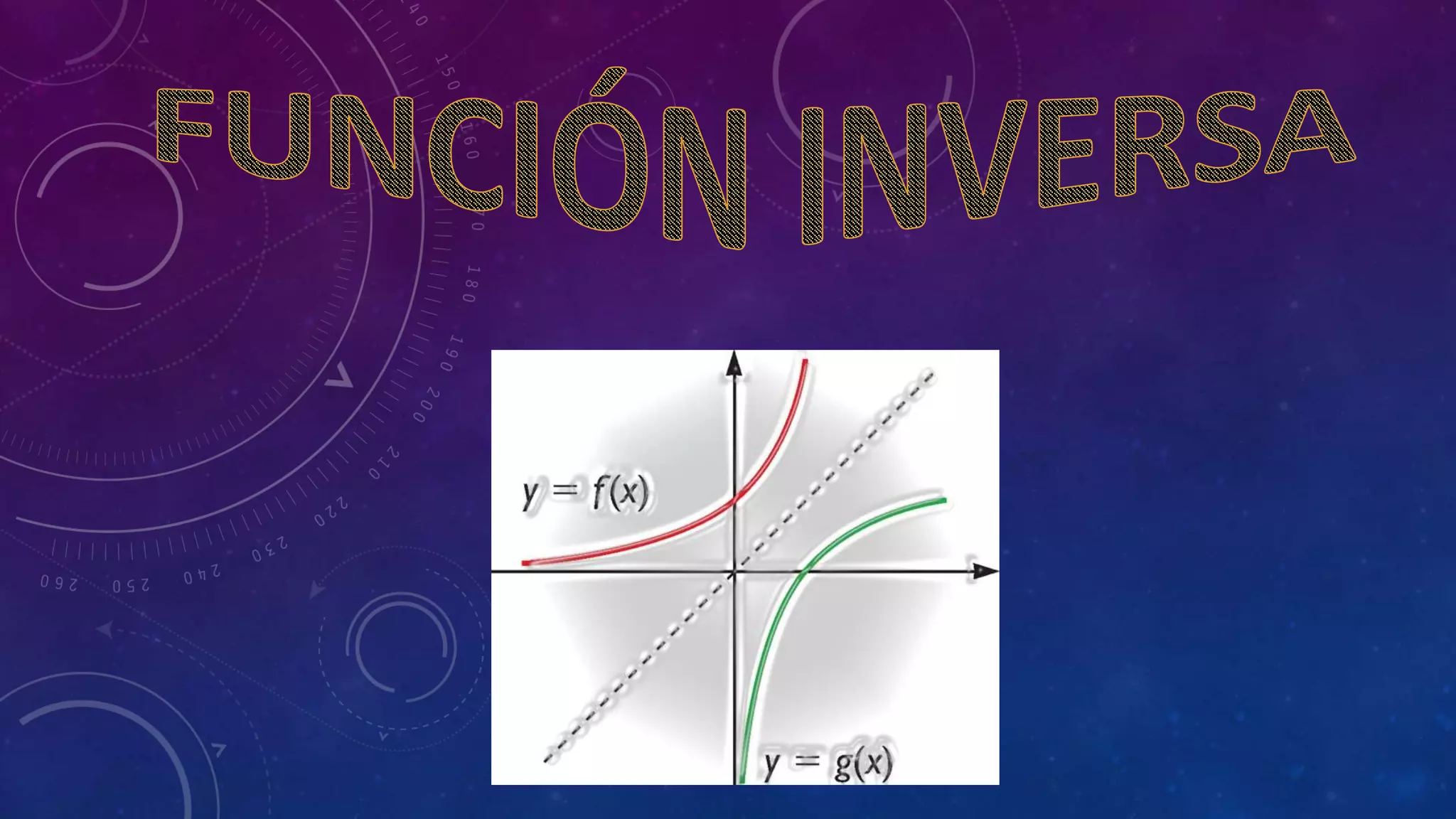
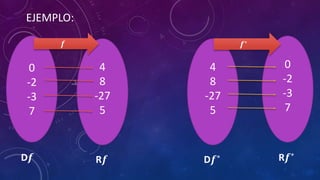
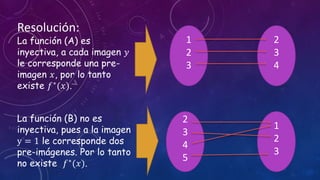
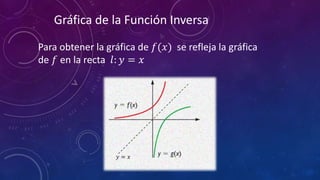
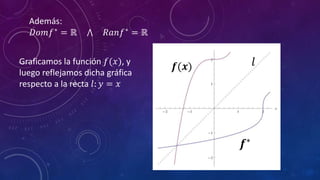
Este documento explica cómo calcular e graficar funciones inversas. Define una función inversa como aquella que intercambia la primera y segunda componente de cada par ordenado de una función biyectiva. Muestra cómo calcular una función inversa despejando la variable y de la función original y luego intercambiando x e y. También explica que para graficar una función inversa se refleja la gráfica de la función original sobre la línea y=x.

2. OBJETIVOS….
Comprender como se obtiene la inversa de las funciones
a partir de la definición.
Saber graficar la función inversa.

3. DEFINICIÓN:
Sea 𝑓 una función biyectiva, entonces 𝑓 posee inversa
denotada por 𝑓−1
o 𝑓∗
y se define de la siguiente manera:
𝑓∗
= 𝑦; 𝑥 𝑦 ∈ 𝑓 𝑥 ; 𝑥 ∈ 𝐷𝑜𝑚𝑓
Establecieno que: 𝐷𝑜𝑚 𝐹∗ = 𝑅𝑎𝑛 𝐹 = 𝑦
𝑅𝑎𝑛 𝐹∗ = 𝐷𝑜𝑚 𝐹 = 𝑥
La inversa de 𝑓 es la función que se obtiene al intercambiar la
primera y segunda componente en cada par ordenado de 𝑓.

4. EJEMPLO:
0
-2
-3
7
4
8
-27
5
4
8
-27
5
0
-2
-3
7
D𝒇 R𝒇 R𝒇∗
D𝒇∗
𝒇∗𝒇

5. Cálculo de la Función Inversa
Si 𝑓 es una función: y = 𝑓(x) biyectiva
I. Se despeja 𝑥 𝑥 = 𝑔(𝑦)
II. Se reemplaza 𝑦 por 𝑥
¿Cuáles de las siguientes funciones tienen inversa?
A. 𝑓 = 1; 2 , 2; 3 , (3; 4)
B. 𝑓 = 2; 1 , 3; 2 , 4; 1 , (5; 3)

6. Resolución:
La función (A) es
inyectiva, a cada imagen 𝑦
le corresponde una pre-
imagen 𝑥, por lo tanto
existe 𝑓∗(𝑥).
1
2
3
2
3
4
La función (B) no es
inyectiva, pues a la imagen
y = 1 le corresponde dos
pre-imágenes. Por lo tanto
no existe 𝑓∗(𝑥).
2
3
4
5
1
2
3

7. Hallar la función inversa de 𝑓 𝑥 = 𝑥 + 3
Resolución:
Comprobamos que 𝑓 𝑥 es
inyectiva:
𝑓 𝑎 = 𝑓(𝑏)
𝑎 + 3 = 𝑏 + 3
𝑎 = 𝑏
Entonces, 𝑓 𝑥 es inyectiva.
𝑎 = 𝑏
Ahora despejamos 𝑥 de la
función:
𝑦 = 𝑥 + 3
𝑥 = 𝑦 − 3
𝑥 = (𝑦 − 3)2
Ahora intercambiamos 𝑥 con 𝑦:
𝑦 = (𝑥 − 3)2
Entonces:
𝑓∗
= (𝑥 − 3)2

8. Gráfica de la Función Inversa
Para obtener la gráfica de 𝑓(𝑥) se refleja la gráfica
de 𝑓 en la recta 𝑙: 𝑦 = 𝑥
𝑦 = 𝑥

9. Ejemplo:
Determinar la función inversa de 𝑓 𝑥 = 𝑥3 + 2 y grafique.
Resolución:
Primero comprobamos si 𝑓(𝑥) es
inyectiva:
𝑓 𝑎 = 𝑓(𝑏)
𝑎3
+ 3 = 𝑏3
+ 3
𝑎3
= 𝑏3
𝑎 = 𝑏
la función 𝑓(𝑥) es inyectiva,
por lo que posee inversa.
Ahora despejamos 𝑥 de la
función:
𝑦 = 𝑥3 + 2
𝑥3 = 𝑦 − 2
𝑥 = 3
𝑦 − 2
Ahora intercambiamos 𝑥 con
𝑦:
y =
3
𝑥 − 2
Entonces:
𝑓∗
=
3
𝑥 − 2

10. Además:
𝐷𝑜𝑚𝑓∗
= ℝ 𝑅𝑎𝑛𝑓∗
= ℝ
Graficamos la función 𝑓(𝑥), y
luego reflejamos dicha gráfica
respecto a la recta 𝑙: 𝑦 = 𝑥
𝒇(𝒙)
𝒇∗
𝑙