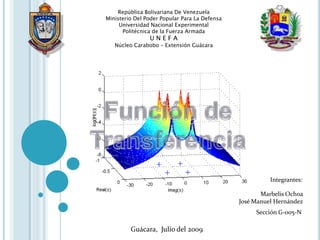
El documento describe las funciones de transferencia, que son modelos matemáticos que relacionan la salida de un sistema con su entrada. Explica que una función de transferencia se define como la transformada de Laplace de la respuesta dividida por la transformada de Laplace de la entrada. También describe formas gráficas de representar funciones de transferencia como diagramas de polos y ceros, diagramas logarítmicos de Bode, y diagramas de Black.

1. República Bolivariana De VenezuelaMinisterio Del Poder Popular Para La DefensaUniversidad Nacional Experimental Politécnica de la Fuerza Armada U N E F ANúcleo Carabobo – Extensión GuácaraFunción deTransferenciaIntegrantes: Marbelis OchoaJosé Manuel HernándezSección G-005-NGuácara, Julio del 2009

2. FUNCIÓN DE TRANSFERENCIAUna función de transferencia es un modelo matemático que a través de un cociente relaciona la respuesta de un sistema (modelado) a una señal de entrada o excitación (también modelado).Por definición una función de transferencia se puede determinar según la expresión:Donde H (s) es la función de transferencia (también notada como G (s) ); Y (s) es la transformada de Laplace de la respuesta y U (s) es la transformada de Laplace de la señal de entrada.Por ejemplo, en análisis de circuitos eléctricos, la función de transferencia se representa como:

3. FUNCIÓN DE TRANSFERENCIAOtro ejemplo de funciones de transferencia es una admitancia o una impedancia:

4. FUNCIÓN DE TRANSFERENCIALa función de transferencia de un sistema:Se usa extensivamente en el análisis y diseño de sistemas lineales invariantes en el tiempo.Es un modelo matemático del sistema, en el sentido de que expresa la ecuación diferencial que relaciona la variable de salida con respecto a la variable de entrada.Es una propiedad del sistema, completamente independiente de la señal de entrada.Relaciona las variables de entrada y de salida, pero no proporciona información sobre la estructura física del sistema.Puede definirse también como la transformada de Laplace de la respuesta al impulso del sistema.Si la función de transferencia de un sistema es conocida, puede estudiarse el comportamiento del sistema para diferentes funciones de entrada.

5. FUNCIÓN DE TRANSFERENCIAREPRESENTACIÓN GRAFICAFormas de representación graficas más usuales de la función de transferencia cuando se trabaja en el dominio de la frecuenciaDIAGRAMA DE POLOS Y CEROS: CASO RACIONALSea la función de transferenciaSe puede representar G(s) indicando la posición de sus ceros –ci y de sus polos –pi en el plano de la variable complejas

6. FUNCIÓN DE TRANSFERENCIAREPRESENTACIÓN GRAFICADIAGRAMA LOGARÍTMICO O DE BODEEn este caso, la función de transferencia G(s) se representa mediante el conjunto de las dos curvas siguientes: Curva de amplitud: Curva de fase:El empleo de logaritmos para representar los módulos permite facilitar la combinación de funciones de transferencia en serie, ya que en tal caso el producto de los módulos se convierte en la suma de sus logaritmos.

7. FUNCIÓN DE TRANSFERENCIAREPRESENTACIÓN GRAFICADIAGRAMA LOGARÍTMICO O DE BODEEste conjunto de curvas, es el más utilizado en la práctica para representar gráficamente la función de transferencia.

8. FUNCIÓN DE TRANSFERENCIAREPRESENTACIÓN GRAFICADIAGRAMA DE BLACKEn este diagrama se representa la función de transferencia G(s) mediante una curva parametrizadaen un plano cuyos ejes de coordenadas están definidos por y

9. FUNCIÓN DE TRANSFERENCIAREPRESENTACIÓN GRAFICADIAGRAMA DE BODELa expresión de la forma de bode es una expresión compleja en función de w. Es decir, para cada valor de tomara un valor complejo y, por tanto, tendrá un modulo y un argumento. El módulo será tal que si tomamos su logaritmo se podrá escribirMientras que el argumento será

10. FUNCIÓN DE TRANSFERENCIAREPRESENTACIÓN GRAFICADIAGRAMA DE BODELa descomposición de las expresión anteriores junto con la que se da de una manera natural para el argumento, permite que se obtenga la representación grafica en el diagrama de Bode a partir de la representación grafica de cada uno de los elementos que aparecen en la expresión de la forma de bodeDIAGRAMA DE BODE DE UNA CONSTANTE

11. FUNCIÓN DE TRANSFERENCIAREPRESENTACIÓN GRAFICADIAGRAMA DE BODEDIAGRAMA DE BODE DE UNA INTEGRACIÓN PURAEl diagrama de Bode de una integración puraViene dada por una recta de pendiente -20 decibelios por década (o -6 decibelios por octava) y con un desfase constante igual a -90 grados

12. FUNCIÓN DE TRANSFERENCIAREPRESENTACIÓN GRAFICADIAGRAMA DE BODEDIAGRAMA DE BODE DE UNA DIFERENCIACIÓN PURAEl diagrama de Bode de un diferenciador puroSe obtiene de forma similar al de un integrador puro. En la figura se representa el diagrama correspondiente. En este caso la curva de amplitud tiene pendiente positiva y la de fase es positiva.

13. FUNCIÓN DE TRANSFERENCIAREPRESENTACIÓN GRAFICADIAGRAMA DE BODEDIAGRAMA DE BODE DEL TERMINO ASOCIADO A UN CEROEl termino asociado a un ceroConduce, por consideraciones análogas a las que se han hecho para un sistema de primer orden (asociado a un polo), tiene la forma que se muestra en la figura