Incrustar presentación
Descargar para leer sin conexión


1. Una función tiene una función inversa si es una función uno a uno, donde el dominio de la función original es igual al rango de la función inversa y viceversa, y ambas cumplen que la composición es la identidad.
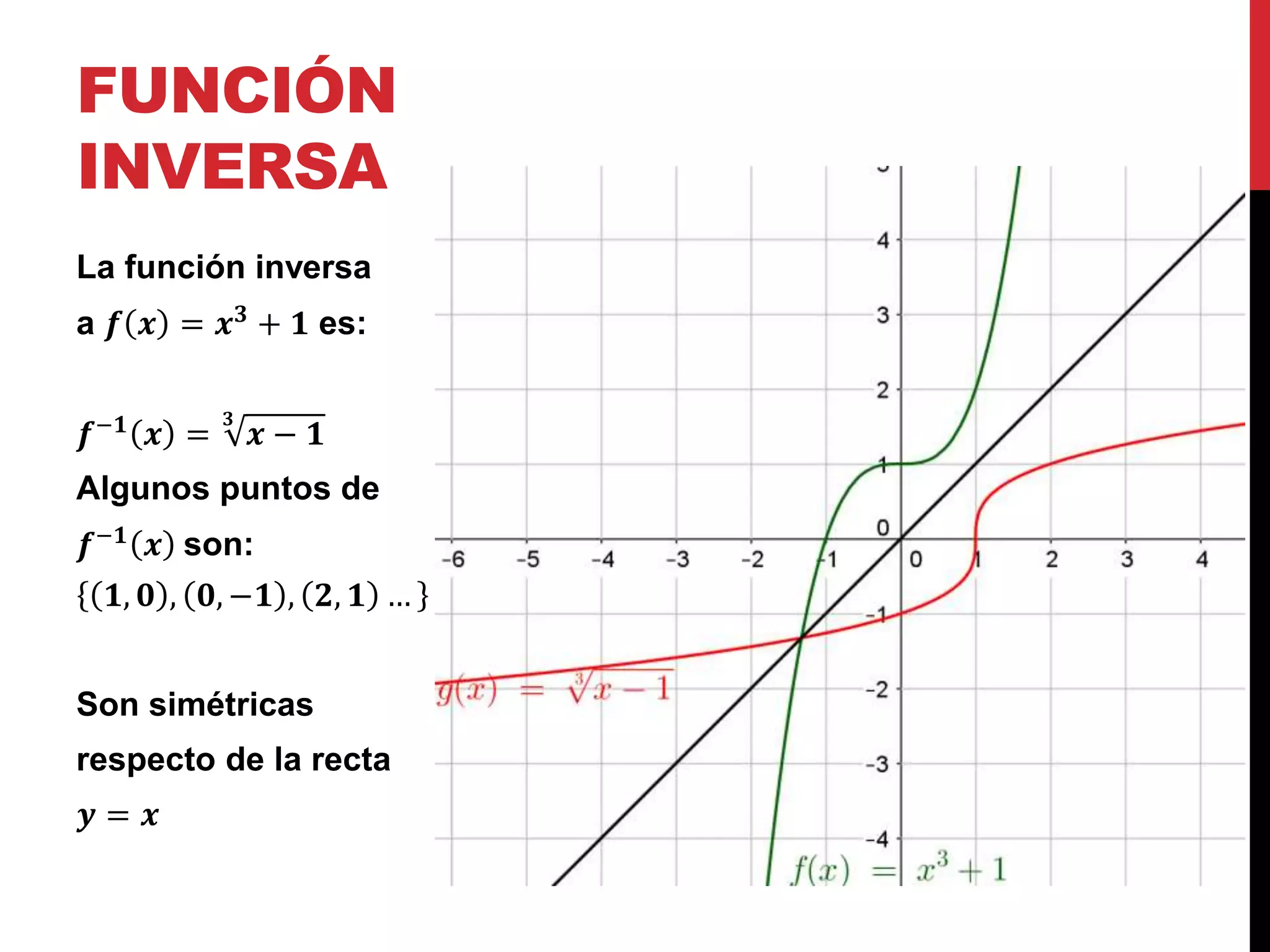
Explora las funciones inversas, características como la simetría respecto a y=x y condiciones para su existencia.
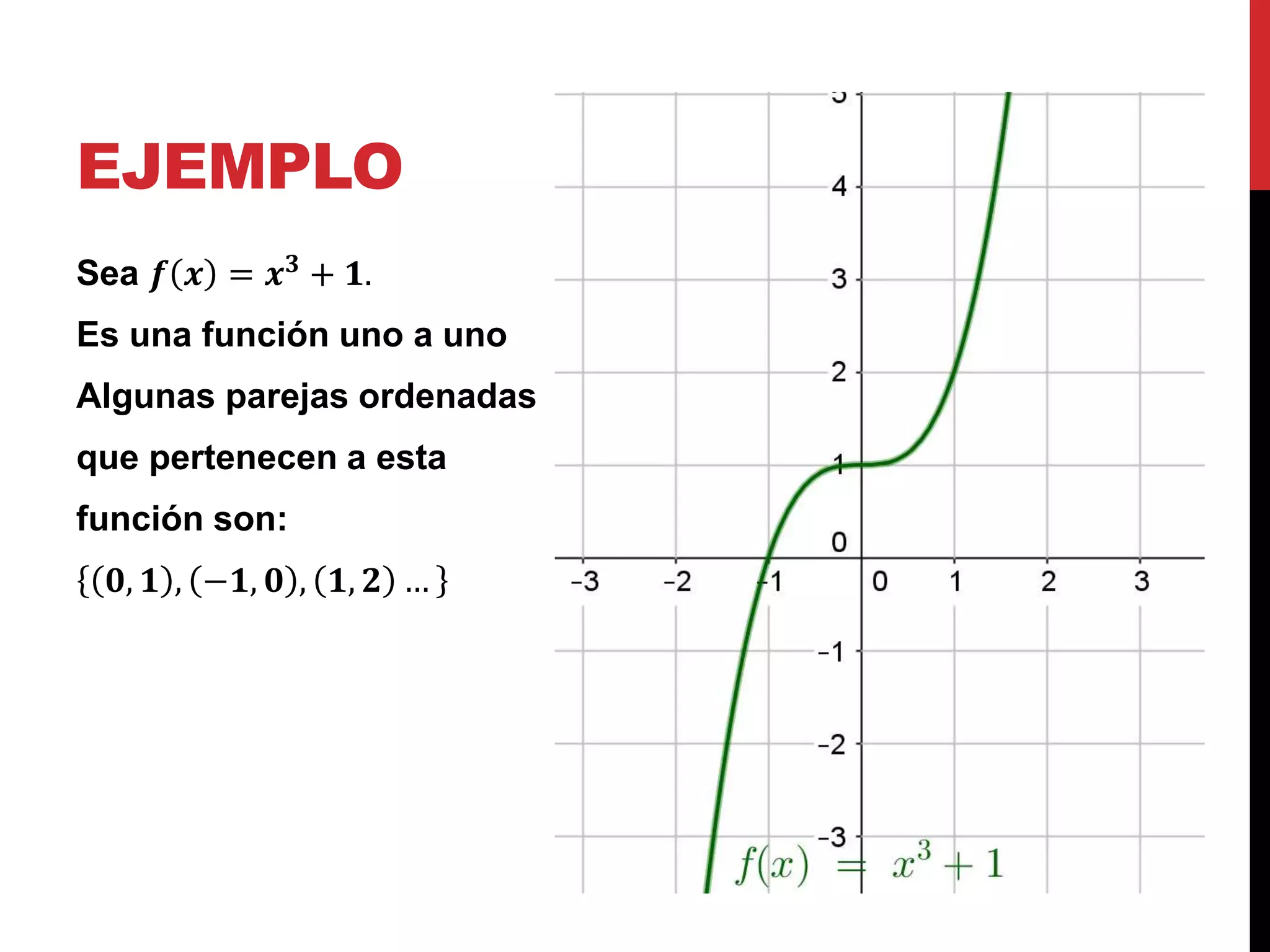
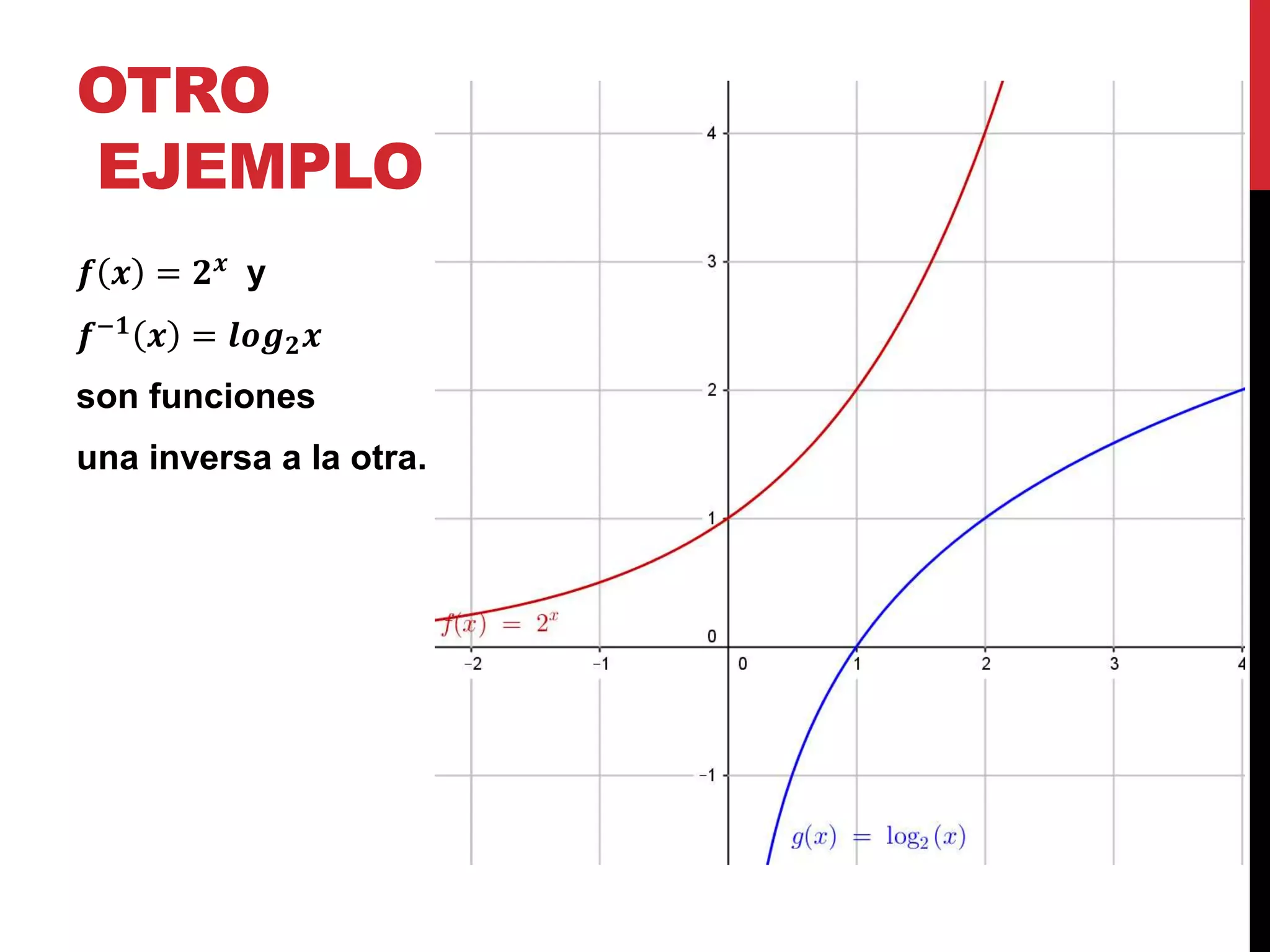
Presenta ejemplos de funciones uno a uno y sus respectivas funciones inversas, mostrando puntos correspondientes.
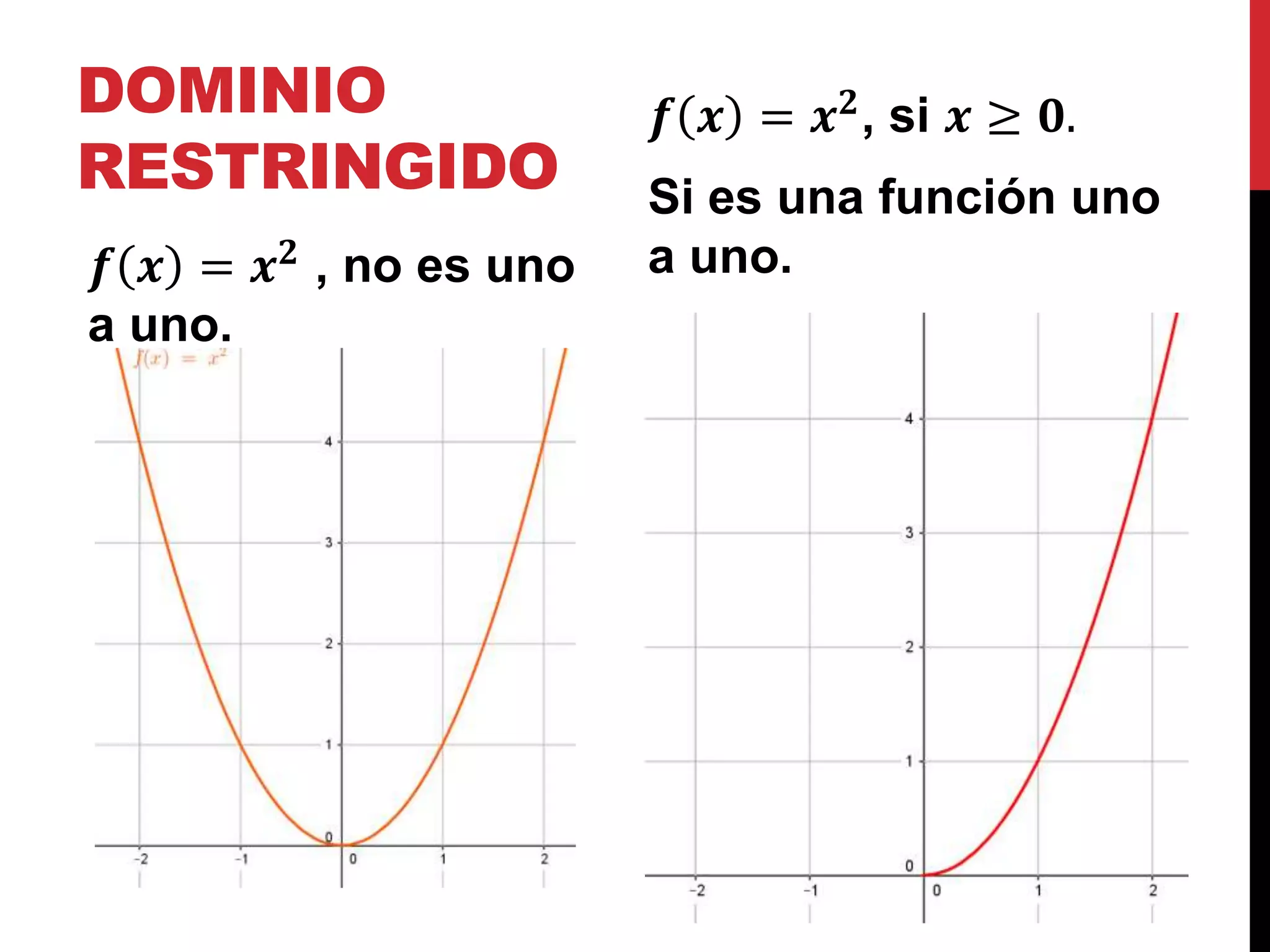
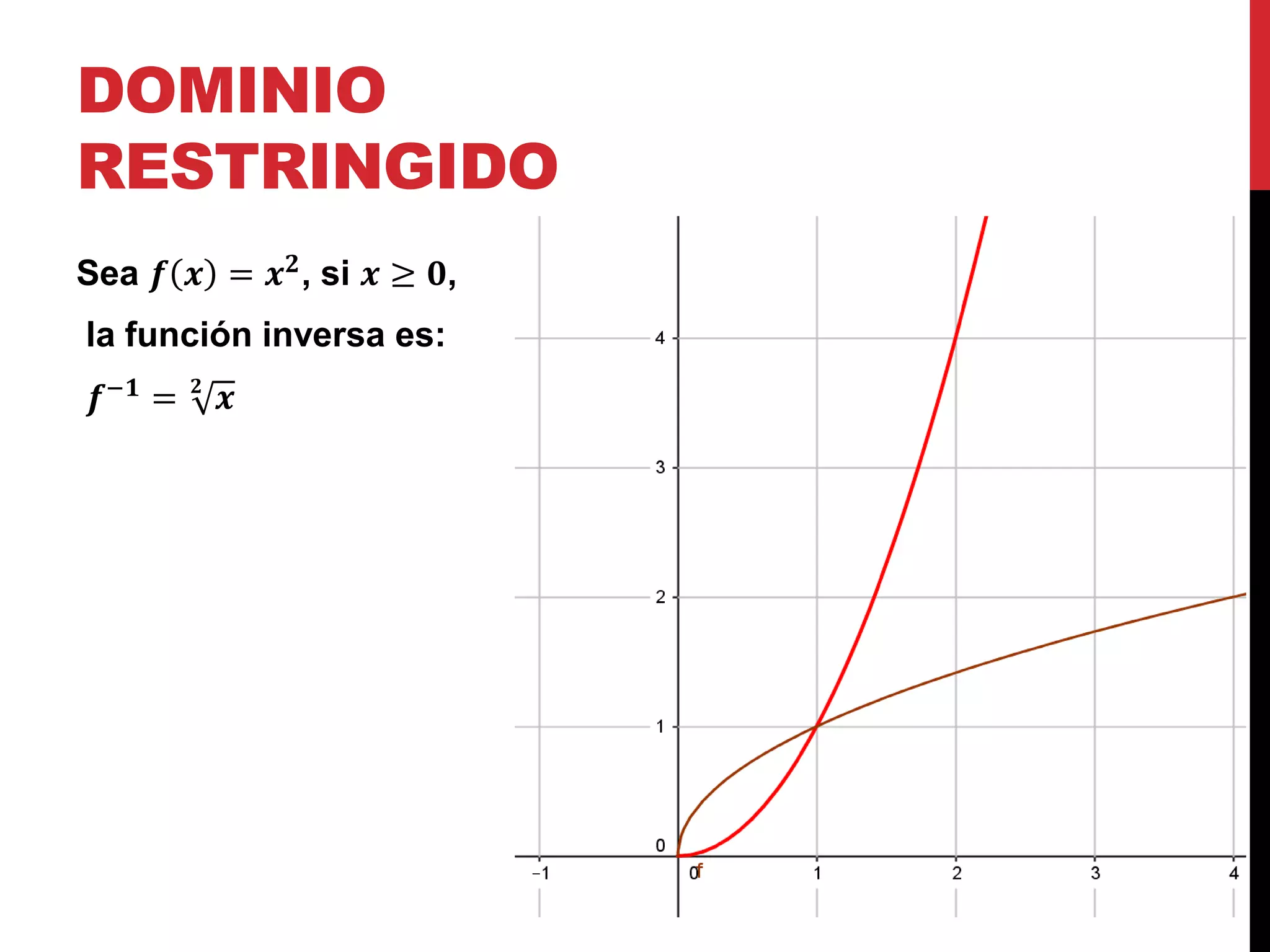
Discute la restricción del dominio en funciones cuadráticas y how se convierte en una función uno a uno.






