El documento aborda la composición de funciones, introduciendo conceptos como (f o g)(x) y (g o f)(x) con ejemplos ilustrativos de diferentes funciones. Además, trata sobre la función inversa, definiéndola y mostrando cómo calcularla con varios ejemplos, y resaltando la simetría de las gráficas de funciones inversas respecto a la bisectriz. Se presentan ejemplos específicos para demostrar la aplicabilidad del concepto y la condición necesaria para que existan funciones inversas.

1. COMPOSICIÓN DE
FUNCIONES
DÍA 33 * 1º BAD CT

2. COMPOSICIÓN DE FUNCIONES
• Sea f(x) y g(x) dos funciones reales de variable real.
• Llamamos función COMPUESTA a alguna de las siguientes expresiones:
• (f o g)(x) = f [ g (x) ]
• (g o f)(x) = g [ f (x) ]
• Ejemplo_1
• Sea f(x) = 1 / x ,, g(x) = x2
- 1
• (f o g)(x) = f [ g (x) ] = 1 / (x2
– 1)
• (g o f)(x) = g [ f (x) ] = (1 / x) 2
– 1 = (1 / x2
) – 1 = ( 1 - x2
) / x2
• Como se ve es muy diferente (f o g)(x) que (g o f)(x)

3. • Ejemplo_2
• Sea f(x) = √ x ,, g(x) = x2
• (f o g)(x) = f [ g (x) ] = √ x2
= x
• (g o f)(x) = g [ f (x) ] = (√ x)2
= x
• Son muy pocas las funciones en que se cumpla (f o g)(x) = (g o f)(x)
• Ejemplo_3
• Sea f(x) = sen x ,, g(x) = x2
– 1
• (f o g)(x) = f [ g (x) ] = sen (x2
– 1)
• (g o f)(x) = g [ f (x) ] = (sen x) 2
– 1
• Como se ve es muy diferente (f o g)(x) que (g o f)(x)

4. • Ejemplo_4
• 3
• Sea f(x) = √ x ,, g(x) = √ x2
• 3 6 3
• (f o g)(x) = f [ g (x) ] = √ (√ x2
) = √ x2
= √ x
• 3 3
• (g o f)(x) = g [ f (x) ] = √ (√ x)2
= √ x
• Son muy pocas las funciones en que se cumpla (f o g)(x) = (g o f)(x)
• Ejemplo_5
• Sea f(x) = sen x ,, g(x) = x2
– 1 ,, h(x) = √x
• (f o g o h)(x) = f [ g (h(x)) ] = sen ((√ x)2
– 1) = sen (x – 1)
• (g o f o h)(x) = g [ f (h(x)) ] = (sen √ x) 2
– 1
• A veces entran en juego tres o más funciones para la composición de las
mismas. Se han hecho dos de los seis ejemplos posibles.

5. FUNCIÓN INVERSA DE OTRA
• Sea y = f(x) una función real de variable real.
• Llamamos función INVERSA a la expresión y = f -1
(x)
• Condición:
• Si f(a) = b  f-1
(b) = a
• Relaciones entre una función y su inversa:
• (f-1
o f )(x) = f-1
[ f (x)] = x
• (f o f-1
)(x) = f [ f-1
(x) = x
• Es decir, que (f-1
o f )(x) = (f o f-1
)(x) = x
•
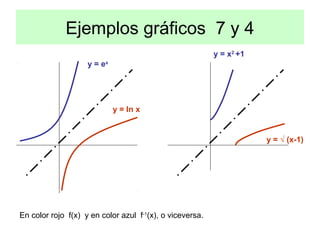
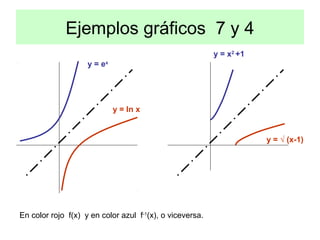
• Las gráficas de dos funciones inversas son simétricas respecto a la
bisectriz del primer cuadrante, o sea respecto a la recta y = x

6. • Para hallar la función inversa, si la tiene, se despeja la variable x en la
ecuación y= f(x) y después se intercambian las x por las y.
• Ejemplo 1
• Sea f(x) = x2
- 1
• y = x2
– 1  x = y2
– 1  y2
= x + 1  y = +/- √(x+1)
• La función resultante No es función, por lo tanto la función dada no tiene
inversa.
• Ejemplo 2
• Sea f(x) = 1 / (x – 2)
• y = 1 / (x – 2)  x = 1 / (y – 2)  x.y – 2.x = 1  y = (1 + 2.x) / x
• Luego f -1
(x) = (1 + 2.x) / x es la inversa de la función dada.
• Comprobemos: (f o f -1
)(x) = 1 / ([(1 + 2.x) / x] – 2) = x
• (f -1
o f)(x) = (1 + 2.[ 1 / (x – 2)]) / [1 / (x – 2)] = x

7. • Ejemplo 3
• Sea f(x) = sen x - 1
• y = sen x – 1  x = sen y – 1  sen y = x + 1  y = arc sen (x + 1)
• Luego f -1
(x) = arc sen (x + 1 )
• Comprobemos: (f o f -1
)(x) = sen [arc sen (x+1)] – 1 = (x + 1) – 1 = x
• (f -1
o f)(x) = arc sen (sen x – 1 + 1) = arc sen (sen x) = x
• Ejemplo 4
• Sea f(x) = √ (x – 1)
• y = √ (x – 1)  x = √ (y – 1)  x 2
= y – 1  y = x2
+ 1
• Luego f -1
(x) = x2
+ 1
• Comprobemos: (f o f -1
)(x) = √ (x2
+ 1 – 1) = √ x2
= x
• (f -1
o f)(x) = [√ (x – 1)] 2
+ 1 = x – 1 + 1 = x

8. Ejemplos gráficos 5 y 6
En color rojo f(x) y en color azul f-1
(x), o viceversa.
y = - 2.x
y = - x / 2
y = 2.x + 1
y = (1/2).x - 2

9. Ejemplos gráficos 7 y 4
En color rojo f(x) y en color azul f-1
(x), o viceversa.
y = ln x
y = ex
y = x2
+1
y = √ (x-1)

10. Ejemplos gráficos 7 y 4
En color rojo f(x) y en color azul f-1
(x), o viceversa.
y = ln x
y = ex
y = x2
+1
y = √ (x-1)