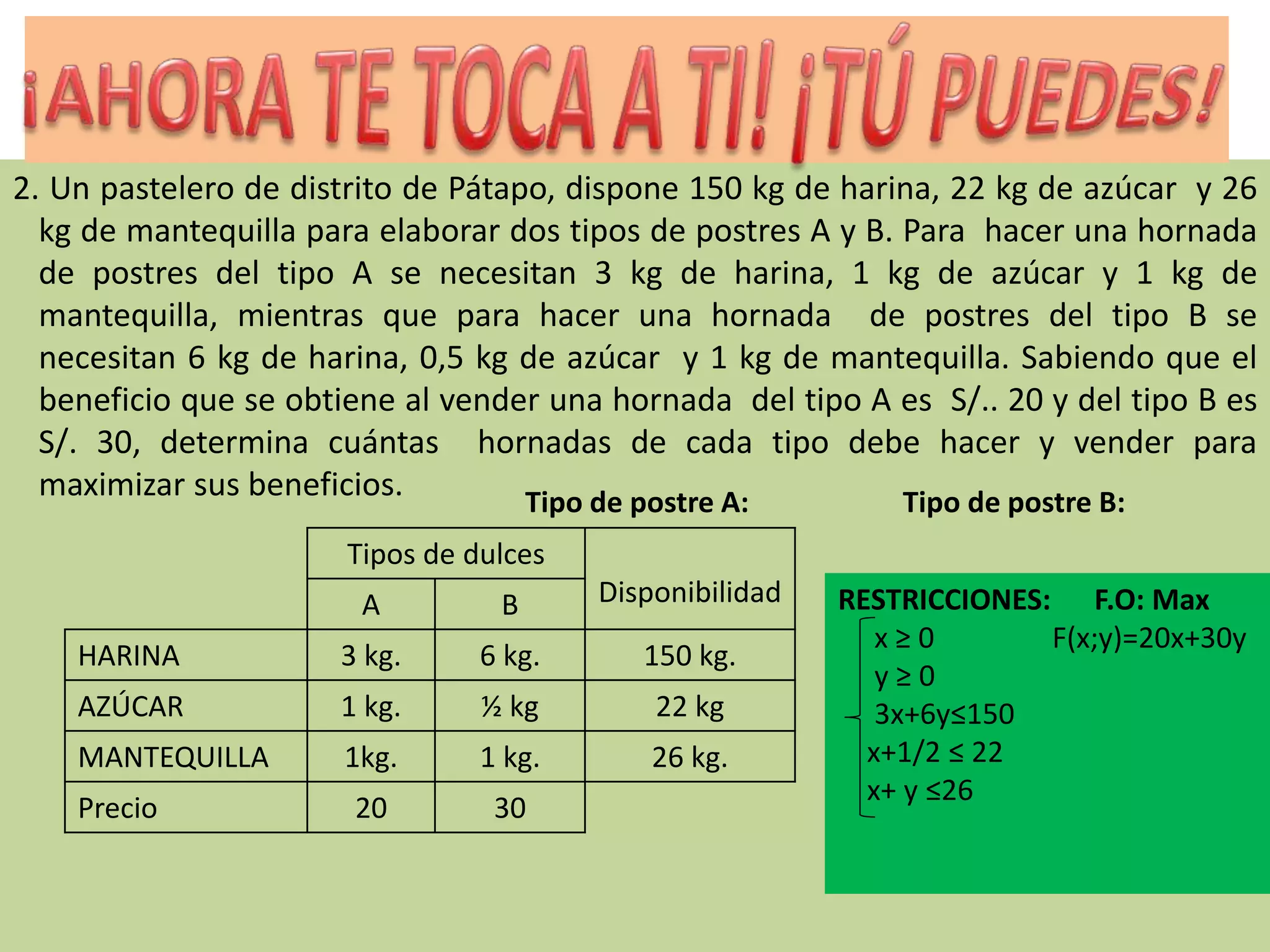
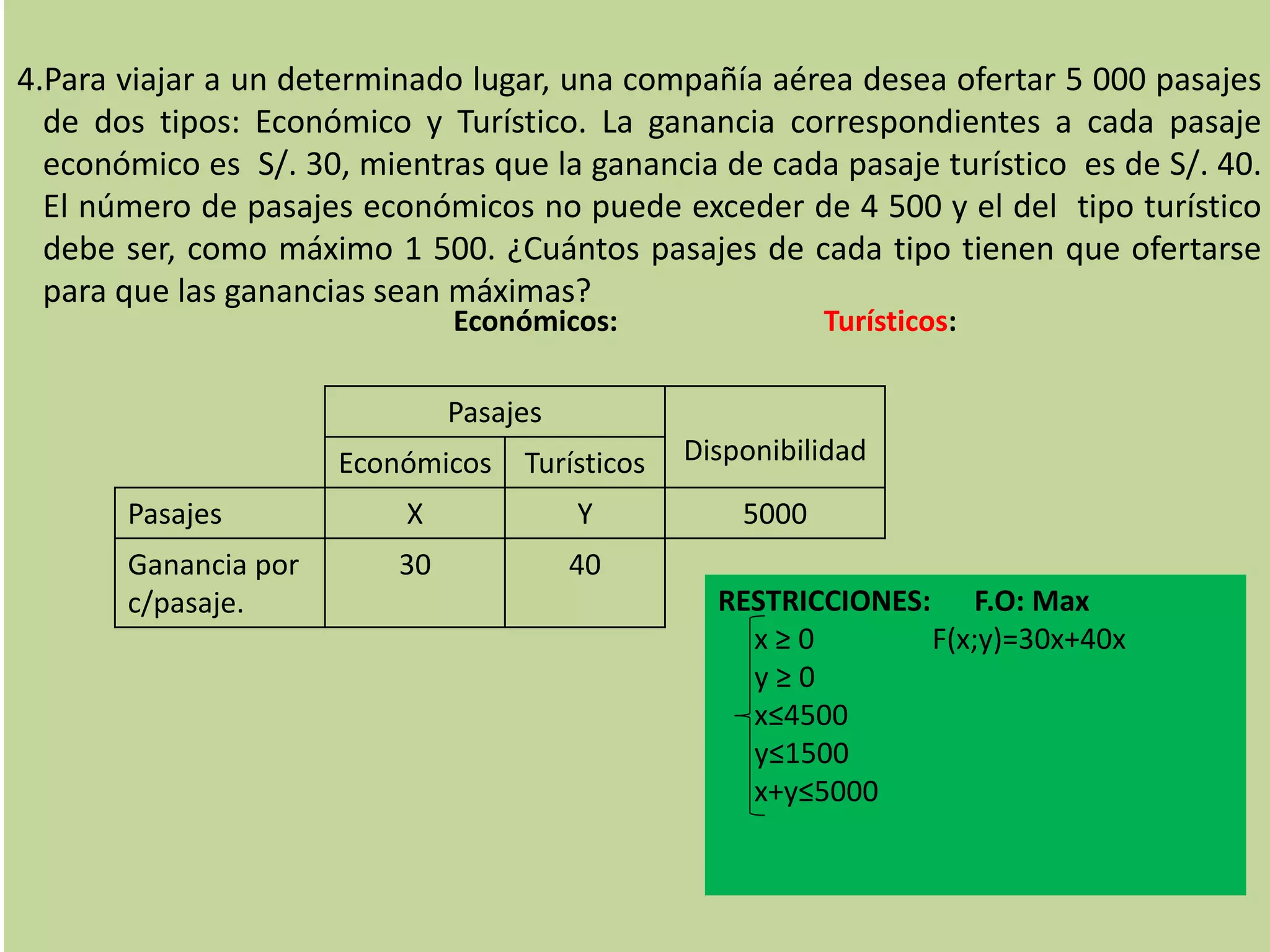
Un pastelero dispone de ingredientes para hacer dos tipos de postres A y B. Para maximizar ganancias, debe determinar cuántas hornadas de cada tipo hacer considerando la disponibilidad de ingredientes y el beneficio por hornada. Se modela el problema como de programación lineal para resolverlo usando Geogebra.

1. DOCENTE: Mag. Zulmy c. López Malahber

2. PROGRAMACIÓN LINEAL CON GEOGEBRA
INGRESO A GEOGEBRA:
1) Clic en el icono que se encuentra en el
escritorio.

3. 2) Leer, comprender, organizar los datos de la situación problemática
en una tabla, definir restricciones y Función Objetivo:
SITUACIÓN PROBLEMÁTICA :
“En la Pastelería “SHADAI” del distrito de Pátapo, se elaboran dulces de fresa y manzana. Cada
dulce de fresa se vende a S/. 12 y requiere 1/2kg. de azúcar y 8 huevos; y cada dulce de
manzana se vende a S/. 15 y requiere 1 kg de azúcar y 6 huevos. En la despensa quedan 10 kg
de azúcar y 120 huevos. ¿Cuántos dulces de cada tipo se deben hacer si pretendemos que los
ingresos por la venta sean máximos?.»
Dulces de Fresa: x Dulces de Manzana: y
Tipos de dulces
DisponibilidadFresa Manzana
Azúcar ½ kg. 1 kg. 10 kg.
Huevos 8 6 120
Precio S/. 12 S/. 15
RESTRICCIONES: F.O: Max
x ≥ 0 F(x;y)=12x + 15y
y ≥ 0
1/2x + 1y ≤ 10
8x + 6y ≤ 120

4. 3) Insertar texto en barra de herramientas (décimo comando),
hacer clic en vista gráfica e insertar las restricciones y la función
objetivo.
4° Desglosar vista gráfica, opción cuadrícula: la vista gráfica aparece
cuadriculado.

5. 5) Insertar en barra de entrada la primera inecuación pero en forma de
ecuación para graficar la recta que la contiene. Luego ir a la vista
algebraica, ubicar el cursor sobre la ecuación, hacer clic derecho, ir a
propiedades de objeto y le damos color. Lo mismo haremos para la
otra inecuación.

6. 6) Insertar en barra de entrada
regfac:(x≥0)˄(y≥0) ˄(1/2x+y≤10)˄(8x+6y≤120), para determinar la
región factible.

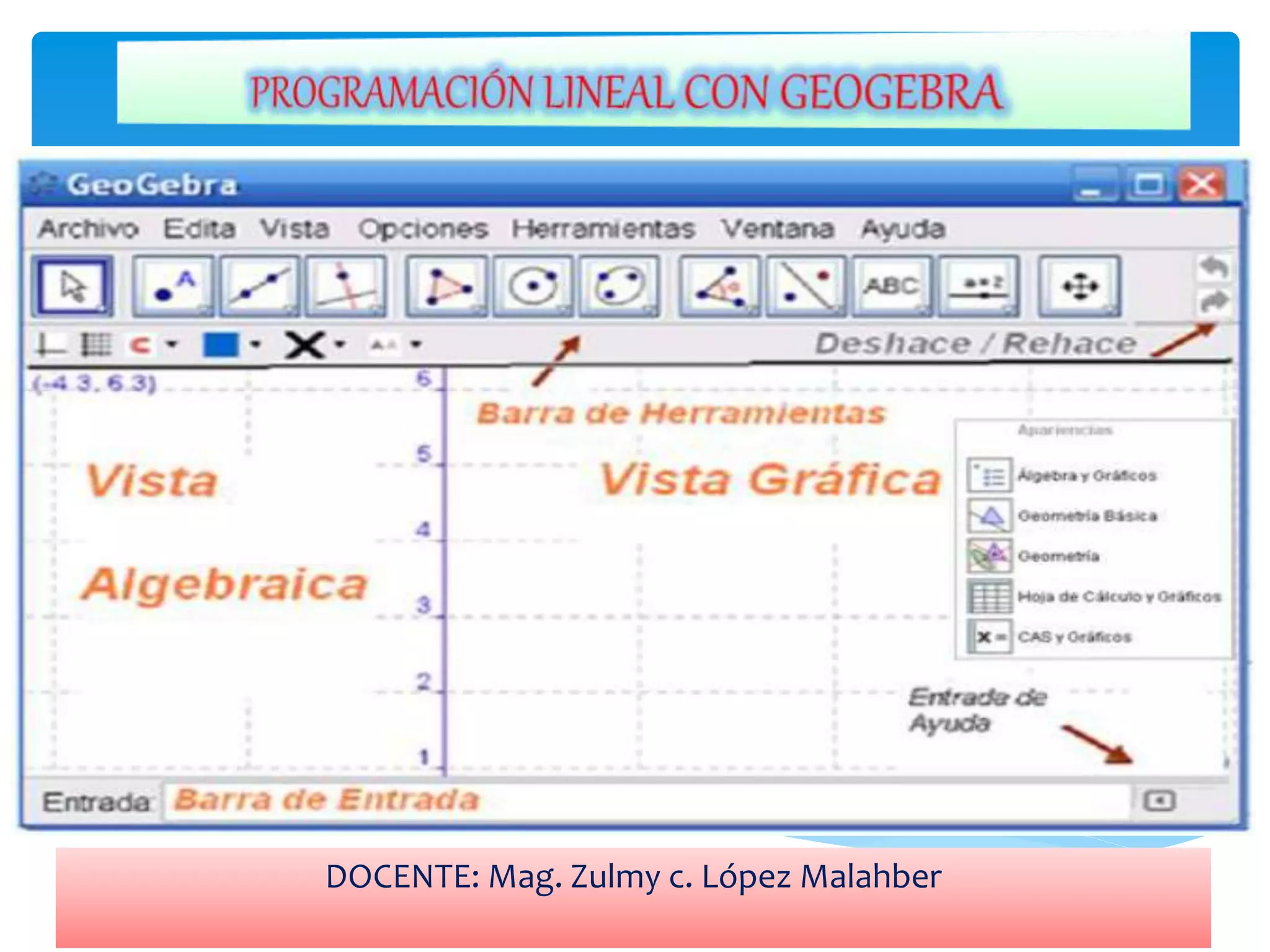
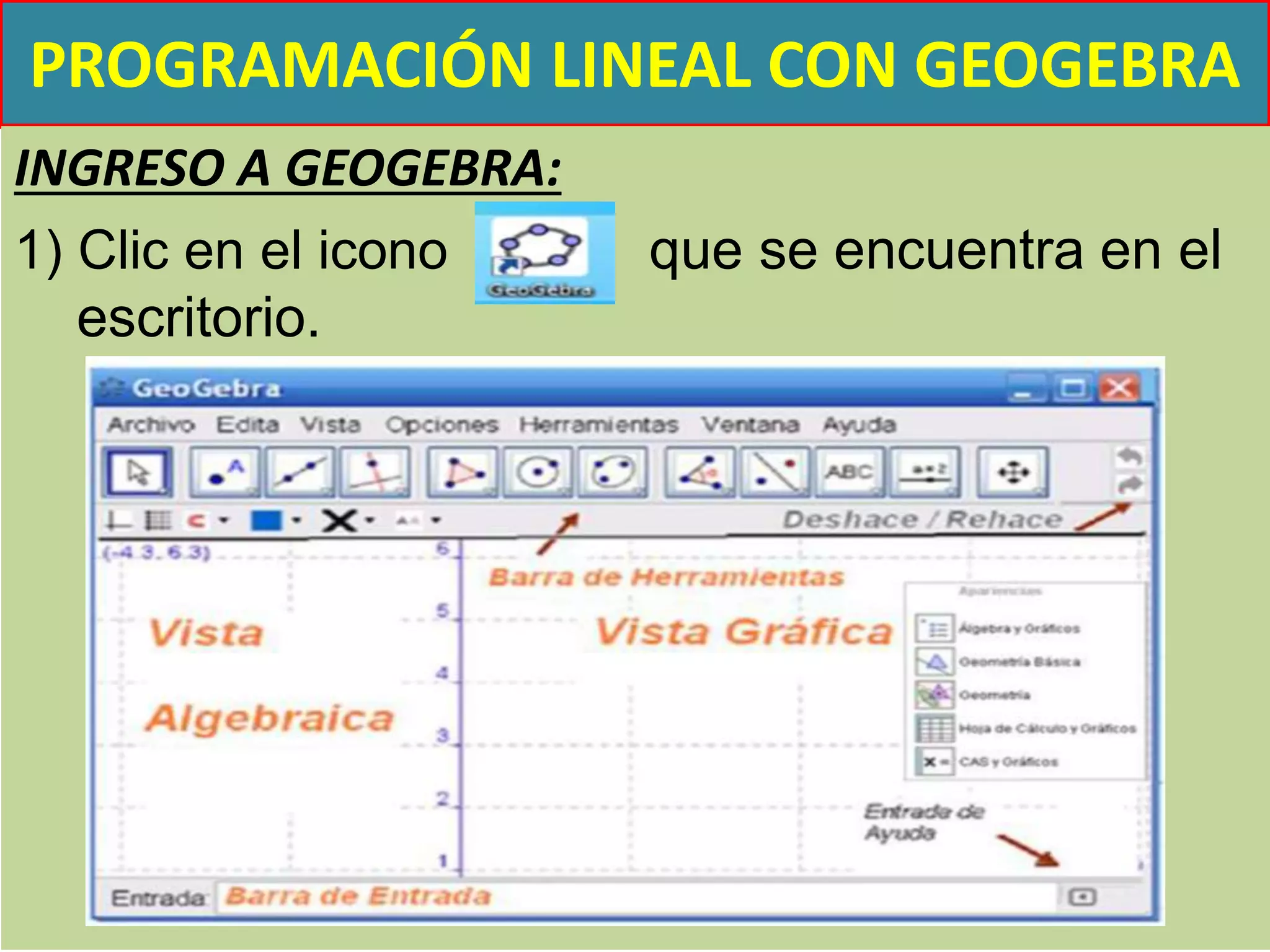
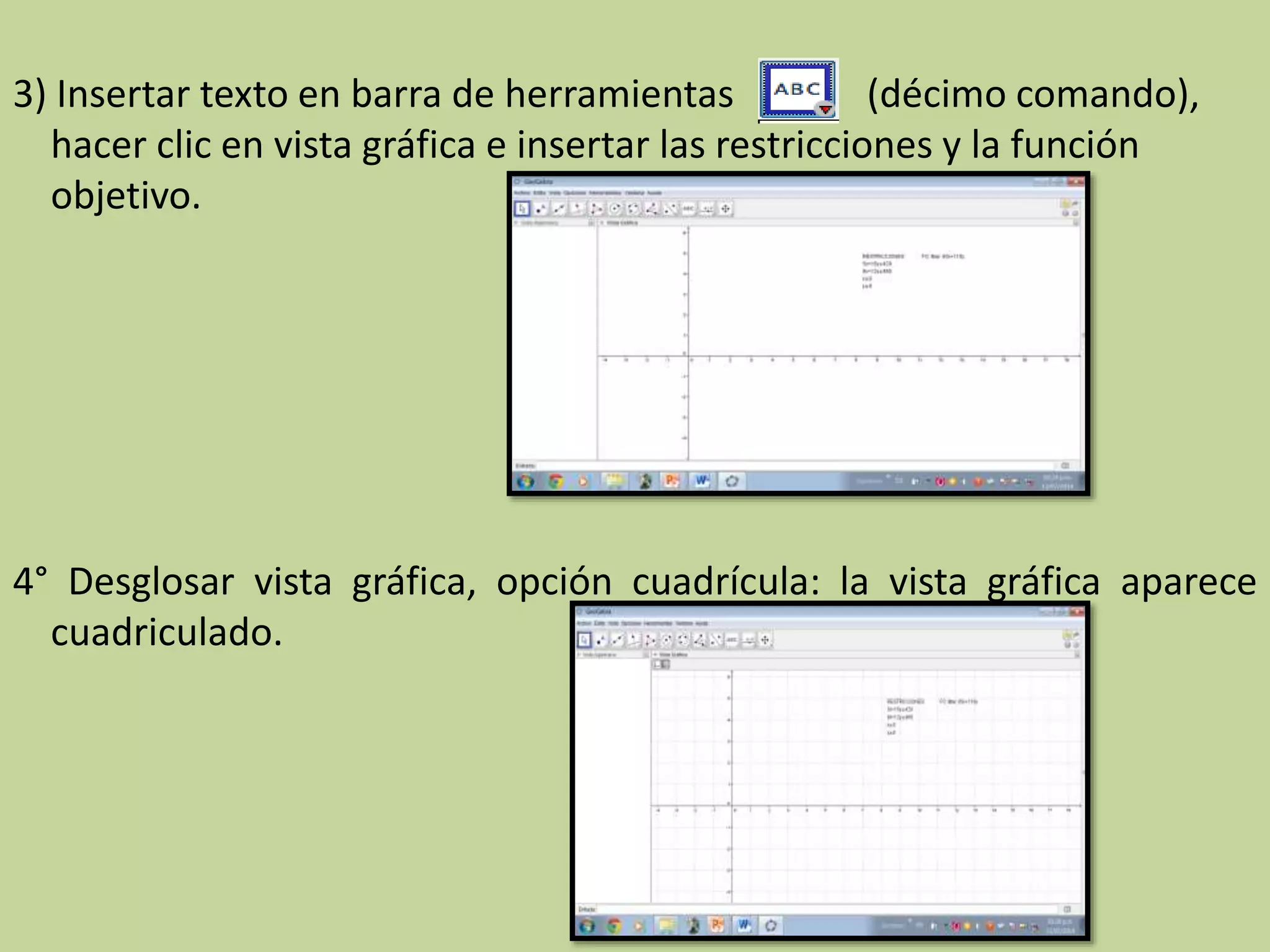
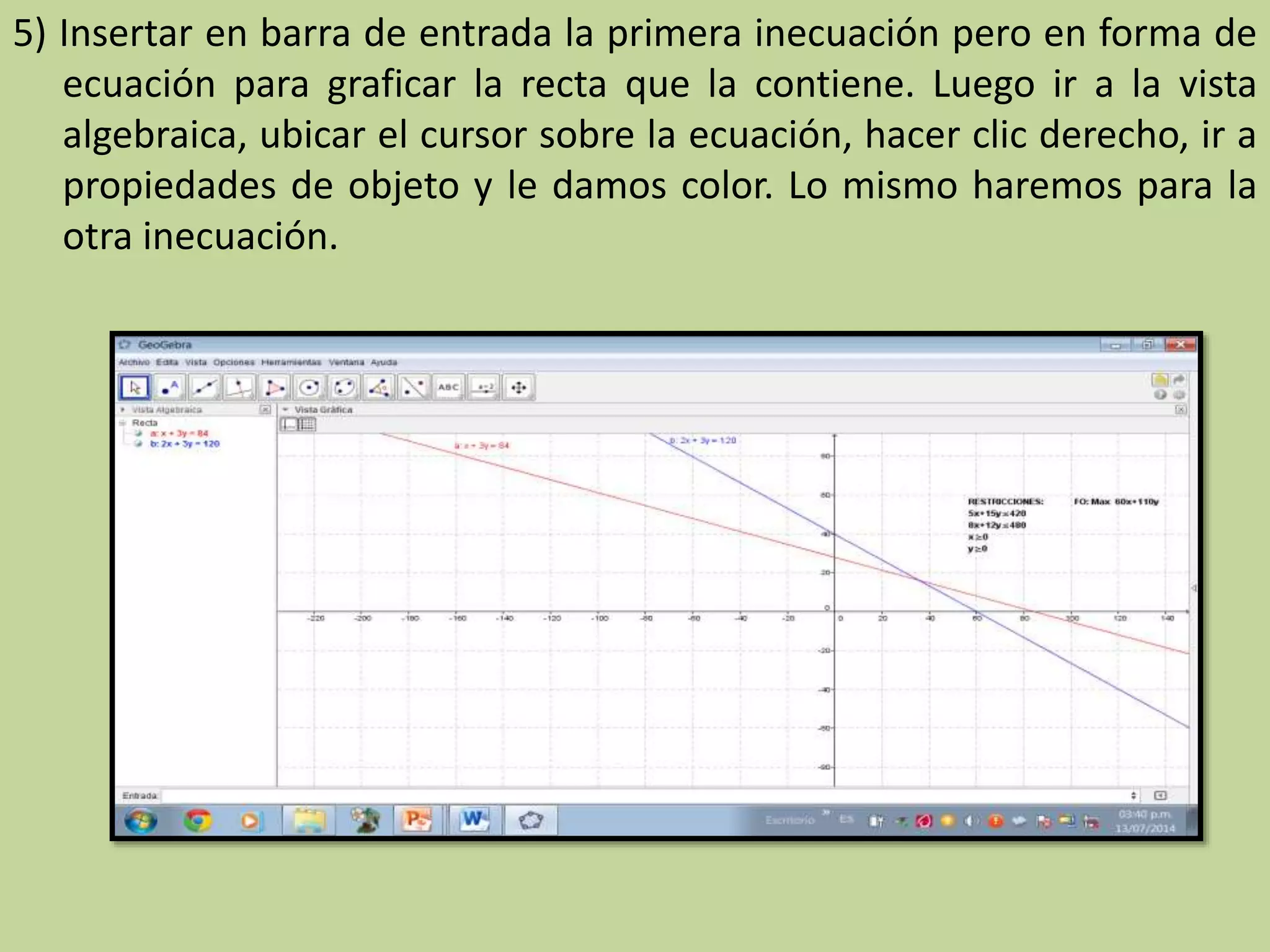
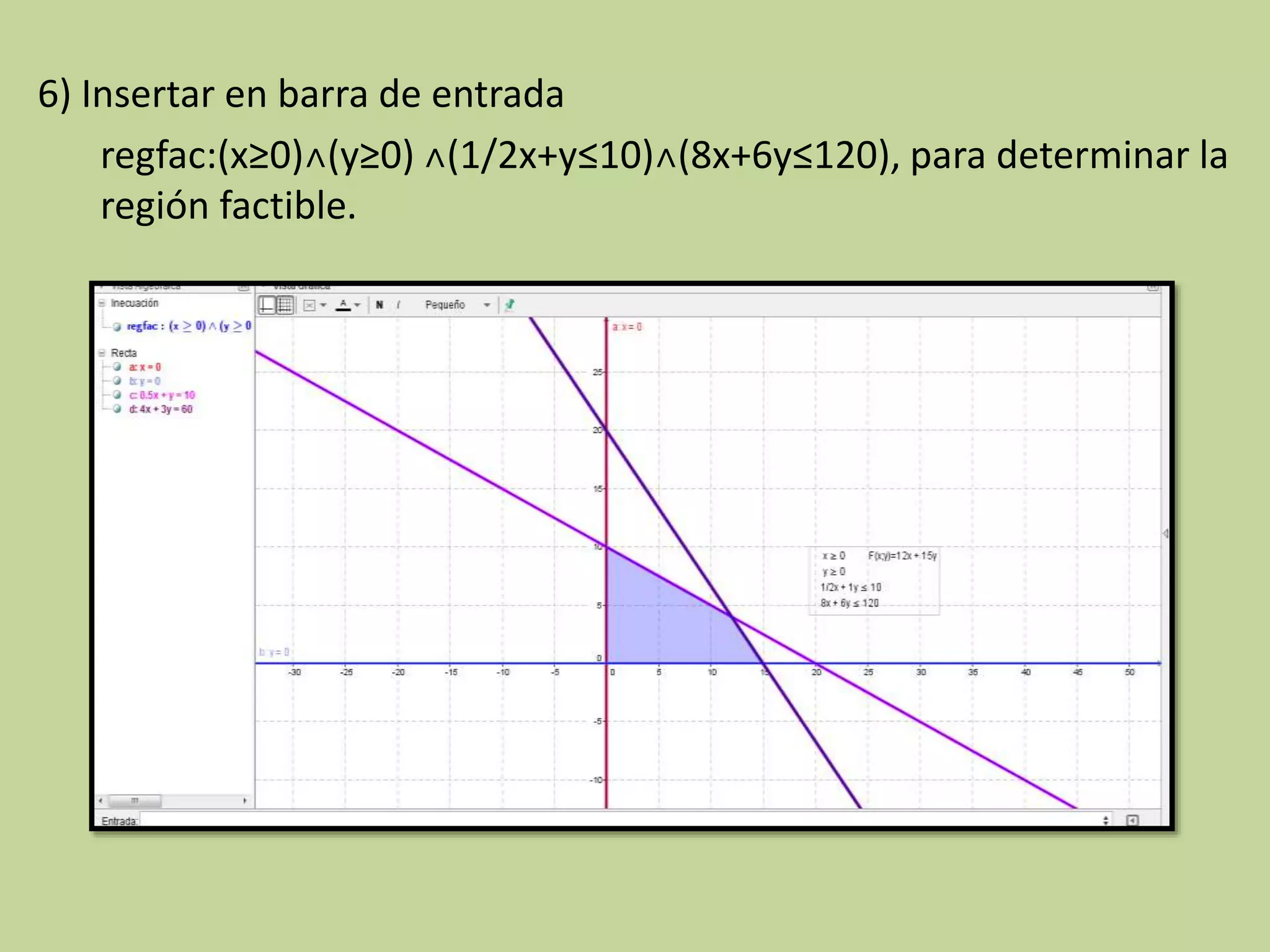
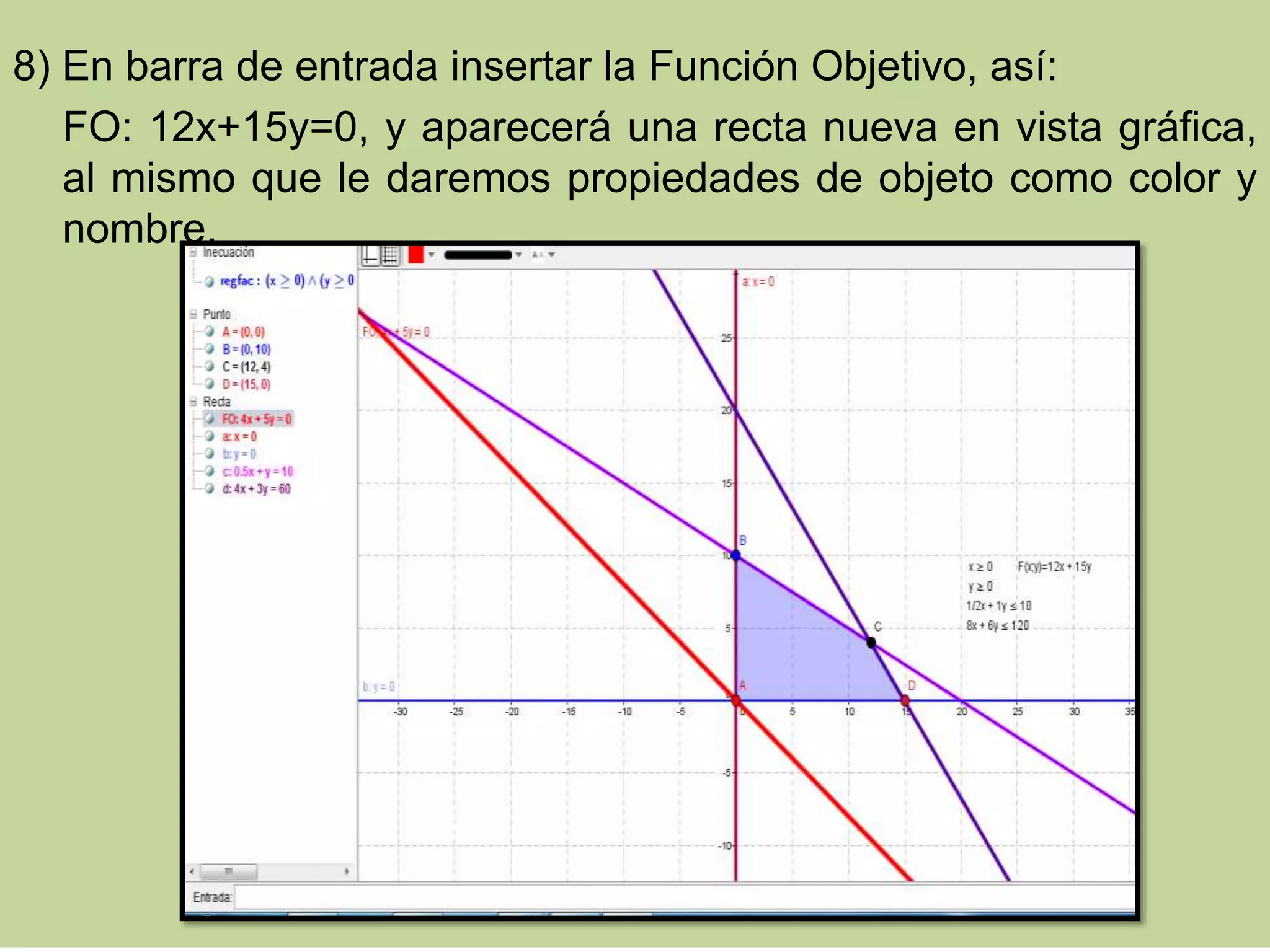
7. 7) Insertar en barra de entrada:
Interseca[a,b], Interseca[a,c], Interseca[c,d],Interseca[b,d]. Para
ubicar los vértices que forman parte de la región factible:

8. 8) En barra de entrada insertar la Función Objetivo, así:
FO: 12x+15y=0, y aparecerá una recta nueva en vista gráfica,
al mismo que le daremos propiedades de objeto como color y
nombre.

9. 9) Ir a barra de herramientas, específicamente al 11avo
comando: deslizador y luego hacer clic en vista gráfica, aparecerá una
tabla, en el nombre escribiremos ValorFO y como Intervalo
consideremos como mínimo 0, como máximo 400 y como incremento
1.

10. 10) Conectar o ligar el deslizador con la función objetivo, haciendo clic
en FO de vista algebraica e ir a propiedades de objeto, en básico
específicamente en definición igualar a ValorFO

11. 11) Haciendo clic en el deslizador notamos que el vértice C es el punto
máximo de nuestra Función Objetivo concluyendo que para obtener
una ganancia máxima se deben fabricar 36 estantes y 16 escritorios.

12. 2. Un pastelero de distrito de Pátapo, dispone 150 kg de harina, 22 kg de azúcar y 26
kg de mantequilla para elaborar dos tipos de postres A y B. Para hacer una hornada
de postres del tipo A se necesitan 3 kg de harina, 1 kg de azúcar y 1 kg de
mantequilla, mientras que para hacer una hornada de postres del tipo B se
necesitan 6 kg de harina, 0,5 kg de azúcar y 1 kg de mantequilla. Sabiendo que el
beneficio que se obtiene al vender una hornada del tipo A es S/.. 20 y del tipo B es
S/. 30, determina cuántas hornadas de cada tipo debe hacer y vender para
maximizar sus beneficios. Tipo de postre A: Tipo de postre B:
Tipos de dulces
DisponibilidadA B
HARINA 3 kg. 6 kg. 150 kg.
AZÚCAR 1 kg. ½ kg 22 kg
MANTEQUILLA 1kg. 1 kg. 26 kg.
Precio 20 30
RESTRICCIONES: F.O: Max
x ≥ 0 F(x;y)=20x+30y
y ≥ 0
3x+6y≤150
x+1/2 ≤ 22
x+ y ≤26

13. 3. Un agricultor tienen 400 hectáreas para sembrar maíz o cebada y dispone de 1200
horas de trabajo durante la temporada. Los márgenes de utilidad para cada uno de
los productos son S/. 60 por hectárea y los requerimientos laborales para trabajar
en la siembra de maíz son 4 horas por hectárea y en la cebada 2 horas por hectárea.
¿Cuántas hectáreas de cada cultivo debe plantar para maximizar su utilidad?
Maíz: Cebada:
Especies
DisponibilidadMaíz Cebada
Cantidad de
hectáreas
X y 400
Horas 4 2 1200
Utilidad / Ha. 60 60
RESTRICCIONES: F.O: Max
x ≥ 0 F(x;y)=60x+60y
y ≥ 0
x+y ≤400
4x+2y≤1200

14. 4.Para viajar a un determinado lugar, una compañía aérea desea ofertar 5 000 pasajes
de dos tipos: Económico y Turístico. La ganancia correspondientes a cada pasaje
económico es S/. 30, mientras que la ganancia de cada pasaje turístico es de S/. 40.
El número de pasajes económicos no puede exceder de 4 500 y el del tipo turístico
debe ser, como máximo 1 500. ¿Cuántos pasajes de cada tipo tienen que ofertarse
para que las ganancias sean máximas?
Económicos: Turísticos:
Pasajes
DisponibilidadEconómicos Turísticos
Pasajes X Y 5000
Ganancia por
c/pasaje.
30 40
RESTRICCIONES: F.O: Max
x ≥ 0 F(x;y)=30x+40x
y ≥ 0
x≤4500
y≤1500
x+y≤5000