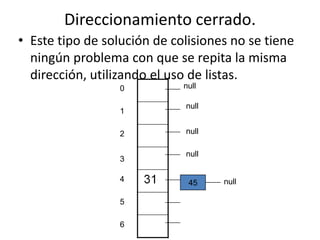
Este documento explica los algoritmos de hash y cómo se utilizan para almacenar y recuperar datos de forma eficiente en O(1). El hashing involucra una función que mapea claves a posiciones de una tabla. Pueden ocurrir colisiones cuando claves diferentes mapean a la misma posición, y existen varios métodos para manejar esto como exploración lineal, cuadrática o doble hash.