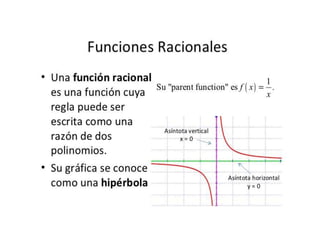
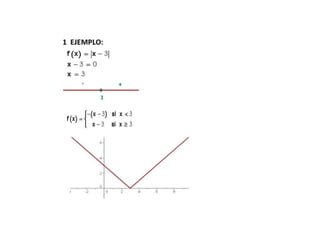
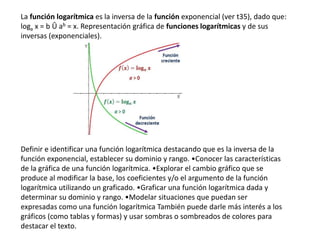
El documento explica las características fundamentales de las funciones, incluyendo que un dominio es el conjunto de valores de entrada y un rango es el conjunto de valores de salida. También describe los dominios y rangos específicos de varios tipos de funciones como funciones trigonométricas, funciones exponenciales y funciones logarítmicas.

1. Participante : Yocdelis Guerra
CI : 15678969

4. Las funciones son correspondencias entre dos conjuntos, llamados dominio
y el rango. Cuando defines una función, normalmente dices qué tipo de
números pueden tener el dominio (x) y el rango (f(x)). Pero incluso si dices
que son números reales, eso no significa que se pueden tomar todos los
números reales para x. Tampoco significa que todos los números reales
pueden ser valores de la función, f(x). Puede haber restricciones en el
dominio y en el rango. Las restricciones dependen parcialmente del tipo de
la función.
En este tema, todas las funciones estarán restringidas a valores de números
reales. Esto es, sólo los números reales pueden ser usados en el dominio y
sólo los números reales pueden estar en el rango. Ejemplo:

5. Las funciones trigonométricas son funciones cuyos valores son extensiones del
concepto de razón trigonométrica en un triángulo rectángulo trazado en una
circunferencia unitaria (de radio unidad).

7. El dominio de una función Trigonométrica : se compone de todos los valores
que se pueden utilizar como entrada a la regla de la función. El dominio es otra
de las características de esa función, porque diferentes funciones tienen
diferentes números que usted puede entrar y tener las salidas tienen ningún
sentido. imagen0.jpg es una función cuyo dominio no puede contener todos los
números negativos, debido a que la raíz cuadrada de un número negativo no es
un número real. La siguiente función tiene un dominio que no se puede incluir el
número -3: image1.jpg Cualquier otro número real está bien, pero no -3, porque
poner un -3 por X hace el denominador igual a 0, y no se puede dividir por 0. (.
Una fracción con un 0 en el denominador representa un número que no existe)
Con funciones trigonométricas, el dominio (valores de entrada) es medidas de
los ángulos - ya sea en grados o radianes. Algunas de las funciones
trigonométricas tienen restricciones en sus dominios, también. Por ejemplo, la
función tangente tiene un dominio que no se puede incluir de 90 grados o 270
grados, entre los muchos otros valores

8. Rango de una función trigonométrica : El rango de una función consiste en
todos sus valores de salida - el número que se obtiene al introducir números
de dominio en la función y realizar las operaciones de función en ellos. A
veces, una serie puede ser todos los posibles números reales - no tiene
límite. Esta situación ocurre en una función tal como h(X) = 3X + 2. En esta
ecuación, tanto el dominio y el rango son ilimitadas. Usted puede poner en
cualquier número real, y se puede obtener una potencia de cualquier
número real que puedas imaginar. Los rangos pueden llegar a ser
restringida, sin embargo. Por ejemplo, la función de k(X) = X2 + 6 siempre
tendrá resultados que son o bien el número 6 o algún número positivo
mayor que 6. Nunca se puede obtener un número negativo o un número
inferior a 6 como una salida. Los rangos de algunas funciones
trigonométricas están restringidas, también. Por ejemplo, la salida de la
función seno nunca excede de 1 o va más baja que -1.

9. Funciones de valor absoluto
Una función de valor absoluto es una función que contiene una
expresión algebraica dentro de los símbolos de valor absoluto.
Recuerde que el valor absoluto de un número es su distancia desde
0 en la recta numérica .
La función padre de valor absoluto, escrita como f ( x ) = | x |, está
definida como :

12. La función exponencial, es conocida formalmente como la función real ex,
donde e es el número de Euler, aproximadamente 2.71828.; esta función
tiene por dominio de definición el conjunto de los números reales, y tiene
la particularidad de que su derivada es la misma función.

13. Consideramos como (dominio y rango de una función exponencial) de igual manera a
aquellos dos conjuntos que definen la dependencia funcional entre valores, en el mismo
contexto que una función matemática común.
Es decir, si nosotros nos disponemos a asignar un valor cualesquiera en lo que se refiere a una
función dicho valor pertenece a un conjunto que hemos denominado como dominio, tal conjunto
es aquel que se encuentra conformado por todos aquellos valores que pueden ser asignados a
la función (o sea puestos en función sobre la misma) y que la función se encuentra definida.
Como conclusión de esa asignación obtenemos otro valor resultado cualesquiera, donde ese
valor obtenido pertenece a otro conjunto que hemos denominado como (rango, imagen o contra
dominio) siendo tal el conjunto conformado por todos aquellos valores resultado o (Producto)
obtenidos de la asignación de los elementos de un dominio.
A esto es lo que denominamos como dominio y rango en general.

14. La función logarítmica es la inversa de la función exponencial (ver t35), dado que:
loga x = b Û ab = x. Representación gráfica de funciones logarítmicas y de sus
inversas (exponenciales).
Definir e identificar una función logarítmica destacando que es la inversa de la
función exponencial, establecer su dominio y rango. •Conocer las características
de la gráfica de una función logarítmica. •Explorar el cambio gráfico que se
produce al modificar la base, los coeficientes y/o el argumento de la función
logarítmica utilizando un graficado. •Graficar una función logarítmica dada y
determinar su dominio y rango. •Modelar situaciones que puedan ser
expresadas como una función logarítmica También puede darle más interés a los
gráficos (como tablas y formas) y usar sombras o sombreados de colores para
destacar el texto.