Este documento presenta los contenidos del primer bimestre de lógica matemática para 5to grado de primaria. Introduce conceptos como teoría de conjuntos, determinación de conjuntos, representación de conjuntos, relación de pertenencia, diagramas de Venn, números naturales, fracciones y decimales. Incluye ejemplos y ejercicios sobre estos temas.



































![LOGICO MATEMATICO– 5º PRIMARIA
- I BIM.
38
I.E.P.
SANTO
TORIBIO
a) A – B b) C – B c) B – D
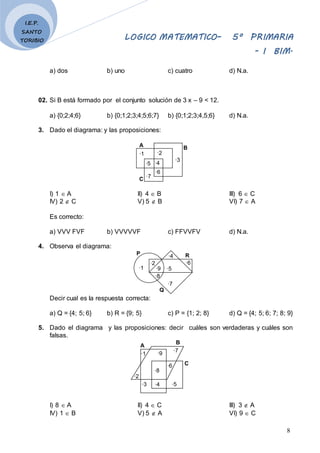
4. Dado el diagrama, escribe V o F:
M N
·c
·b
·d
S
·i
·a
·u
·o
·e
M – N = {b, d, c, e} .... ( ) N – S = {a, o, u} .... ( )
S – M = {b, c, d, e} ..... ( ) N – M = {a, o, u} .... ( )
5. Dado los conjuntos:
U = Universal = { x N / x < 10}
A = { x B / B = <3; 7] }
C = { x2 – 3 / x N 2 x 3 }
Hallar:
a) A b) CB c) (A B) d) [ (A B) – C ]
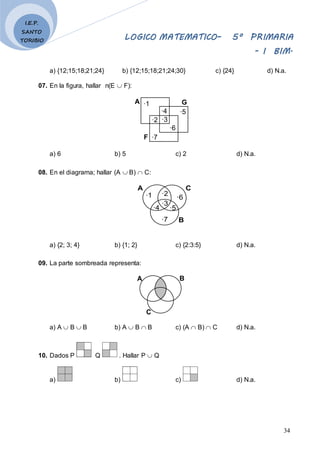
6. Dado el diagrama, efectuar:
·e
Q ·f
·g
·b
·c
·a
·d
M P
M P = P Q =
P M = Q P =](https://image.slidesharecdn.com/ibimestre-220606021628-1d272978/85/I-BIMESTRE-doc-38-320.jpg)






























































































































































































![LOGICO MATEMATICO– 5º PRIMARIA
- I BIM.
234
I.E.P.
SANTO
TORIBIO
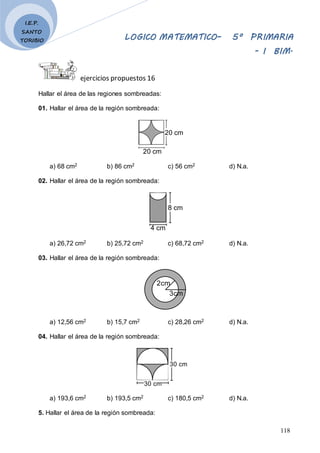
ejercicios propuestos n°14
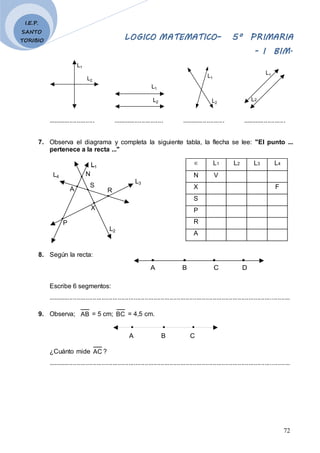
01. Resolver 25
,
0
15
2
x
4
3
a) 0,25 b) 0,35 c) 3,05 d) N.A.
02. En la sucesión 0,5; 1,2; 2; 2,9 .......... el número que sigue es:
a) 3 b) 3,8 c) 3,9 d) N.A.
03. Los 0,75 de 0,05 de 0,2 de 0,3 de 400 es:
a) 0,9 b) 900 c) 9 d) N.A.
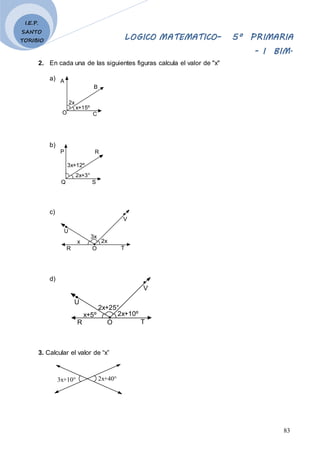
04. Si es a como es a ...
a) b) c) d) N.A.
05. Sea suma = 2375, El valor de (s + u + m + a) es :
a) 15 b) 16 c) 17 d) N.A.
TAREADOMICILIARIA
Resolver las operaciones combinadas.
a) (5,94 - 0,87) x 16
b) 7,06 x (12,94 + 24,06)
c) (25,6 + 5,447) x (3,81 + 3,19)
d) (18,4 x 5) : (36,4 x 2)
e) [1,8 + (5,6 : 7) - 0,6] : 10
f)
4
,
0
:
16
,
1
x
10
1
2
1
g)
8
,
0
7
,
1
7
,
0
25
,
0
:
4
1 2
2
](https://image.slidesharecdn.com/ibimestre-220606021628-1d272978/85/I-BIMESTRE-doc-234-320.jpg)




















