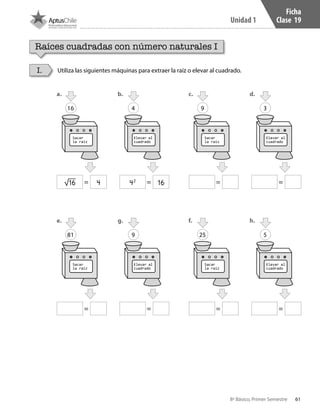
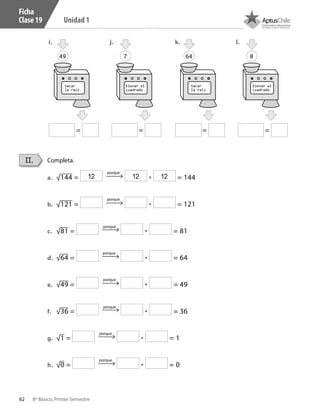
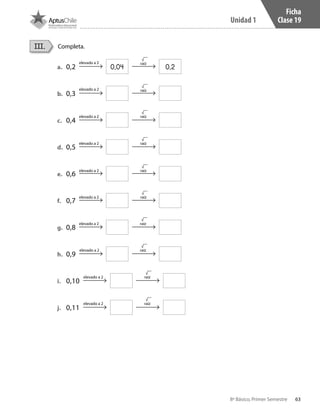
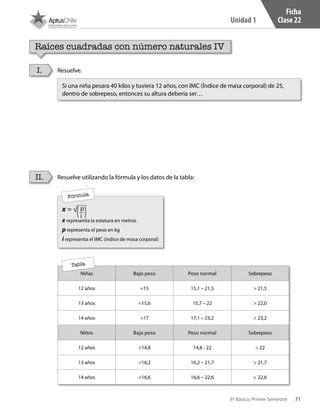
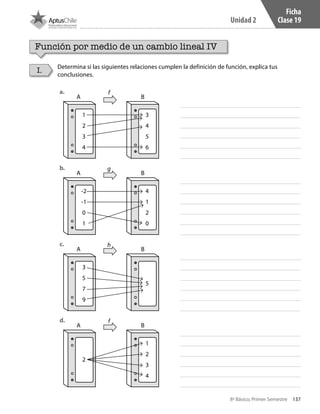
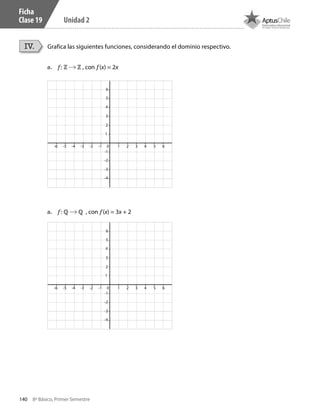
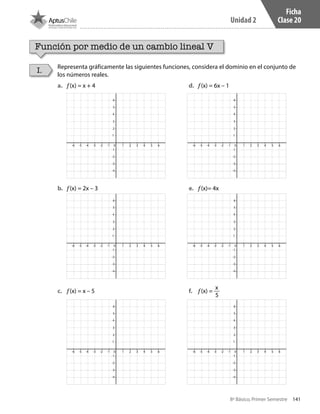
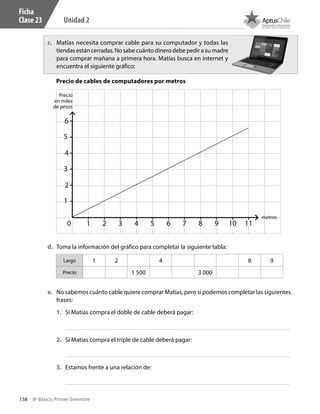
Este documento presenta un cuaderno de trabajo de matemáticas para estudiantes de 8° básico en Chile. Incluye 5 unidades con ejercicios de multiplicación y división de números enteros resueltos usando la recta numérica. El documento contiene créditos de la imagen de portada y no presenta más información relevante en 3 oraciones o menos.
















![16 8º Básico, Primer Semestre
Unidad 1
Ficha
Clase 5
Usando el orden de operatorias, resuelve los siguientes ejercicios.
Resuelve los siguientes ejercicios, considerando el orden de las operatorias.
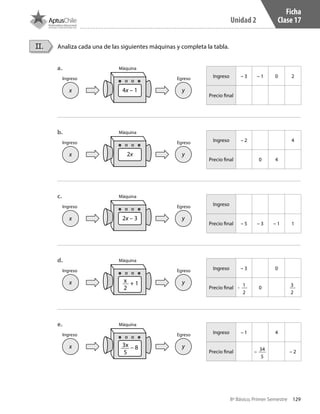
II.
III.
a. 18 + (–12 – 3) =
b. 18 + (– 5) • (18 – 6) =
c. 20 + (– 4) • (3 – 6) =
d. –19 + (7 • 4) =
e. –19 – (–3) + (–2) • (8 – 4) =
f. – 3 + 2 • (– 6 : 3) =
a. 7 + [– 12 • (– 1)] – 8 =
b. 8 – (– 7) + (– 13 + 3) =
c. 5 – (– 8) : 2 =
d. 17 – (-3)
-2
=
e. – 8 • (– 2) – (2) =
f. [(– 8) + 5] + (12 – 18) =
CT 8º I SEM 2017.indb 16 20-10-16 17:25](https://image.slidesharecdn.com/cuadernodetrabajo-primersemestre-191003212734/85/Matematica-8-Basico-tomo-1-18-320.jpg)





![22 8º Básico, Primer Semestre
Unidad 1
Ficha
Clase 6
Determina el valor de [2x : y –(y)], dados los siguientes valores. Considera el orden de las
operatorias.
¿Dónde se deben poner los paréntesis para obtener el resultado indicado?
IV.
V.
a. x = (– 4 + 2), y = (+ 1 + 6 : (– 2))
b. x = (– 4 • 2), y = (+ 2 • (– 2))
c. x = (– 4 – 2), y = (– 2 + 1)
d. x = (18 : (– 2)), y = (– 9 : (– 3))
a. - 15 + 5 • 3 = – 30
b. 400 – 80 : 20 + 12 =10
c. 12 – 3 • 49 – 4 • 9 =117
CT 8º I SEM 2017.indb 22 20-10-16 17:25](https://image.slidesharecdn.com/cuadernodetrabajo-primersemestre-191003212734/85/Matematica-8-Basico-tomo-1-24-320.jpg)




![29
Unidad 1
8º Básico, Primer Semestre
Ficha
Clase 8
Resuelve los siguientes ejercicios utilizando la regla punto antes que línea o bien respetando
el uso de paréntesis.
Determina la incógnita que permite obtener el resultado indicado.
III.
IV.
a. (– 3) • – – – =
b. [3 • – ] – – =
c. [(– 1) • – ] + [1 • ] =
d. (-2) : – – =
a. 2
7
5 – 2
7
= 8
7
b. (-2) : – – = 2
c. 3 1
2
– 1
2
= 1
d. + 3
5
– 3 + 9
5
= 0
e. 3 1
2
– 1
2
= 1
f. 10 • 3
5
+ = 2
1
4
2
4
3
4
1
5
1
3
2
5
2
5
2
5
1
2
CT 8º I SEM 2017.indb 29 20-10-16 17:25](https://image.slidesharecdn.com/cuadernodetrabajo-primersemestre-191003212734/85/Matematica-8-Basico-tomo-1-31-320.jpg)






![39
Unidad 1
8º Básico, Primer Semestre
Ficha
Clase 11
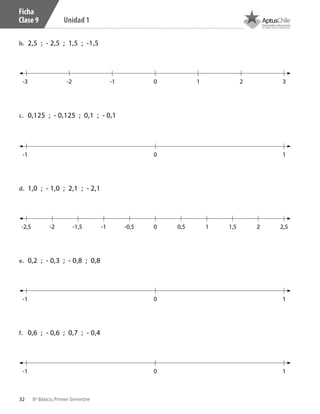
Ubica en la recta numérica los siguientes valores.
Resuelve los siguientes ejercicios utilizando la regla punto antes que línea o bien respetando
el uso de paréntesis.
IV.
V.
a. - 2 ; 0 ; - 1 ; 1 ; 1
2
; - 1
2
; 0,25 ; - 2,5
b. - 15
20
; 15
20
; - 1
4
; 1
4
a. (– 3) • (– 0,25) – (– 0,5 ) =
b. [(3) • (– 2
5
)] – (– 0,2 ) =
c. (– 2) : (0,75) – (– 1
3
) =
d. 7 + (– 4
3
• – 36
4
) – 8 =
e. 2,5 – (– 7
2
) + (– 1, 3) =
f. – 12
3
– (– 8) : 2 =
g.
1
4
– (– 2
5
)
– 2
=
-3
-3 -2 -1 0 1
CT 8º I SEM 2017.indb 39 20-10-16 17:26](https://image.slidesharecdn.com/cuadernodetrabajo-primersemestre-191003212734/85/Matematica-8-Basico-tomo-1-41-320.jpg)