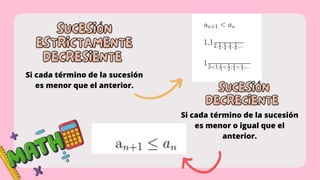
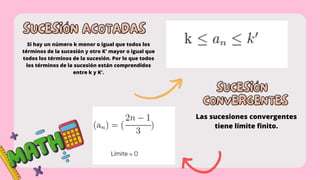
Este documento presenta información sobre sucesiones y progresiones matemáticas. Explica conceptos como inducción matemática, técnicas de conteo, sucesiones, progresiones aritméticas y geométricas. Define cada uno de estos conceptos y ofrece ejemplos ilustrativos.

1. UNIVERSIDAD CENTRAL DEL ECUADOR
FACULTAD DE FILOSOFÍA, LETRAS Y CIENCIAS DE LA EDUCACIÓN
PEDAGOGÍA DE LAS CIENCIAS EXPERIMENTALES QUÍMICA Y
BIOLOGÍA
INTEGRANTES:
-CHRISTIAN CACUANGO
-MELANIE CASA
-MICHAEL CASTILLO
-JESSICA ROMÁN
-JANIS SILVA
TEMA:
Inducción matemática
Técnicas de conteo
sucesiones y progresiones Aritméticas y Geométricas

2. Es un método de demostración
utilizado para establecer la
veracidad de una afirmación
INDUCCIÓN A LA
INDUCCIÓN A LA
MATEMÁTICA
MATEMÁTICA

3. Demostrar que la sustentación es
verdadera para el número natural
más pequeño (generalmente 0 o 1)
PASO BASE
PASO BASE
Demostrar que la sustentación es
verdadera para el número natural
más pequeño (generalmente 0 o 1)

4. Suponer que la obtenida es
verdadera para un número natural
cualquiera y demostrar que también
es verdadera para su sucesor n+1.
PASO INDUCTIVO
PASO INDUCTIVO

5. Es un conjunto ordenado de números
llamados términos, que se designan
con una letra y un subíndice .
SUCESIÓN
SUCESIÓN
Ejemplo:

3,6, 9...,3n

6. SUCESIÓN
SUCESIÓN
ESTRICTAMENTE
ESTRICTAMENTE
CRECIENTE
CRECIENTE
Una sucesión es estrictamente
creciente si cada término es
mayor que el anterior.
SUCESIÓN CRECIENTE
SUCESIÓN CRECIENTE
Una sucesión es creciente si
cada término es mayor o igual
que el anterior.

7. SUCESIÓN
SUCESIÓN
ESTRICTAMENTE
ESTRICTAMENTE
DECRESIENTE
DECRESIENTE
Si cada término de la sucesión
es menor que el anterior.
SUCESIÓN
SUCESIÓN
DECRECIENTE
DECRECIENTE
Si cada término de la sucesión
es menor o igual que el
anterior.

8. SUCESIÓN
SUCESIÓN
CONSTANTE
CONSTANTE
Si todos su términos son
iguales.
SUCESIÓN ACOTADAS
SUCESIÓN ACOTADAS
INFERIORMENTE
INFERIORMENTE
Si todos sus términos son
mayores o iguales que un cierto
número K, que llamaremos cota
inferior de la sucesión.

9. SUCESIÓN ACOTADAS
SUCESIÓN ACOTADAS
Si hay un número k menor o igual que todos los
términos de la sucesión y otro K' mayor o igual que
todos los términos de la sucesión. Por lo que todos
los términos de la sucesión están comprendidos
entre k y K'.
SUCESIÓN
SUCESIÓN
CONVERGENTES
CONVERGENTES
Las sucesiones convergentes
tiene límite finito.

10. SUCESIÓN
SUCESIÓN
DIVERGENTES
DIVERGENTES
Son las sucesiones que no
tienen límite finito.
SUCESIÓN
SUCESIÓN
OSCILANTES
OSCILANTES
No son convergentes ni
divergentes. Sus términos
alternan de mayor a menor o
viceversa.

11. Son estrategias matemáticas usadas en
probabilidad y estadística que permiten
determinar el número total de
resultados que puede haber a partir de
hacer combinaciones dentro de un
conjunto o conjuntos de objetos.
TÉCNICAS DE CONTEO
TÉCNICAS DE CONTEO

12. Es el número de maneras distintas en que se
pueden ordenar los elementos de un conjunto.
PERMUTACÍON
PERMUTACÍON
Con
repetición
Sin
repetición

13. Se ordenan un total
de n elementos
distintos.
Se ordenan un total de n elementos,
siendo a de un tipo, b de otro, c de
otro, y así con el resto de elementos
Sin
repetición
Con
repetición
Pn=n!
Por ejemplo:
Ordenar las letras de la palabra
MURCIELAGO
Por ejemplo:
Ordenar las letras de la palabra MATEMATICA

14. Ejemplo de Sin repetición :
¿Cuántos números de tres cifras diferentes se pueden formar con los dígitos
1,2,3?
Con repetición:
¿Cuántas palabras de cinco letras pueden formarse usando tres veces la letra
A y dos veces la B?
EJERCICIOS
EJERCICIOS

15. Una combinación es una disposición de elementos
sin un orden en particular.
COMBINACÍON
COMBINACÍON
Con
repetición
Sin
repetición

16. De un total de n elementos
distintos, se escoge r
elementos sin importar el
orden.
De n tipos de elementos, se escogen r
elementos que pueden repetirse, sin
importar el orden.
Sin
repetición
Con
repetición
Por ejemplo:
Escoger 3 personas de un total
de 7.
Por ejemplo:
Escoger 3 bolitas de una bolsa con bolitas
de dos colores.

17. Ejemplo de Sin repetición :
En una tienda hay cinco pelotas de distintos colores, si queremos comprar
tres pelotas diferentes, ¿Cuántas combinaciones podemos formar?
Con repetición:
En un tren hay pasajeros de 3 nacionalidades diferentes, se elige a 5 de
ellos para realizar una encuesta. ¿De cuantas formas diferentes pueden
resultar las nacionalidades de los seleccionados?
EJERCICIOS
EJERCICIOS

18. Una progresión geométrica es una sucesión de números reales llamados
términos que se obtiene multiplicado el término anterior por una
constante denominada razón.
PROGRESIONES GEOMÉTRICAS
PROGRESIONES GEOMÉTRICAS

19. La constante que multiplicamos a cada término para obtener el siguiente
se denomina RAZÓN (r) de la progresión geométrica
La posición del término en una progresión geométrica representamos por
(n)
La forma general para representar una progresión geométrica a1, a2, a3,
a4, a5,…… así sucesivamente.
La progresión geométrica está definida por la fórmula
general:
Donde
an es el término en la posición n.
a1 es el primer término de la progresión
r es la razón común de la progresión
n es la posición del término en la secuencia

20. ·Progresión geométrica creciente
En este caso la razón es mayor a 1 (r ˃1 ) y los términos de
la progresión son positivos, cuando 0 es menor que razón y
menor que 1 (0 ˂ r ˂ 1), y los términos de la progresión son
negativo.
Ejemplo: La sucesión 2,4,8,16………. Es una progresión
geométrica de r=2 donde la r ˃1.
La sucesión -12, -6, -3 … es una progresión geométrica de
r= ½ donde 0 ˂ r ˂ 1
TIPOS
TIPOS
PROGRESIONES GEOMÉTRICAS CRECIENTE
PROGRESIONES GEOMÉTRICAS CRECIENTE

21. ·En este caso 0 ˂ r ˂ 1 y los términos son
positivos o cuando r ˃1 y los términos son
negativos.
Ejemplos
La sucesión 128, 64, 32… es una progresión
geométrica de r= ½ donde 0 ˂ r ˂ 1
La sucesión -3, -6, -12………. Es una progresión
geométrica de r=2 donde la r ˃1
PROGRESIÓN GEOMÉTRICA DECRECIENTE
PROGRESIÓN GEOMÉTRICA DECRECIENTE

22. En este caso la razón es uno ( r=1)
Ejemplo
La sucesión 10,10,10, …… es una progresión
geométrica de r=1
• PROGRESIÓN GEOMÉTRICA CONSTANTE
• PROGRESIÓN GEOMÉTRICA CONSTANTE

23. Cuando r ˂ 0
La sucesión 5, -10, 20,…. Es una progresión
geométrica de r=-2
• PROGRESIÓN GEOMÉTRICA ALTERADA
• PROGRESIÓN GEOMÉTRICA ALTERADA

25. PROGRESIONES ARITMÉTICAS
PROGRESIONES ARITMÉTICAS
Una progresión aritmética es una sucesión de números tales que cada uno
de ellos (salvo el primero) es igual al anterior más un número fijo llamado
diferencia que se representa por "d ".
DIFERENCIA
La diferencia entre ambos términos es una constante, que puede ser
positiva o negativa.
Ejemplo:
12, 14, 16... La diferencia es +2, entonces es positiva
21, 18, 15, 12.....La diferencia es -3, entonces es negativa

26. FÓRMULA
FÓRMULA
Fórmula término general
an = a1 + (n-1)d
Para hallar el término enésimo de una progresión aritmética se aplica la
fórmula del término general:
an: término enésimo
a1: primer término
n: número de términos
d: diferencia de la progresión

27. PARA CALCULAR
PARA CALCULAR
Para calcular el término general:
1. Si conocemos el 1er término.
El término general está dado por la fórmula an= a1+(n-1)d
Ejemplo:
Progresión aritmética: 8, 3, -2, -7, -12...
Diferencia: -5
Primer término: 8
an= a1+(n-1)d
Término general : an= 8+(n-1)(-5)= 8-5n+5=-5n+13 SUCESIÓN
Para calcular el término general:
1. Si conocemos el 1er término.
El término general está dado por la fórmula an= a1+(n-1)d
Ejemplo:
Progresión aritmética: 8, 3, -2, -7, -12...
Diferencia: -5
Primer término: 8
an= a1+(n-1)d
Término general : an= 8+(n-1)(-5)= 8-5n+5=-5n+13 SUCESIÓN

28. PARA CALCULAR
PARA CALCULAR
2. Si conocemos el valor que ocupa cualquier otro término de la progresión.
El término general está dado por la fórmula: an= ak +(n-k) d
Ejemplo:
Progresión aritmética: _, 3, -2, -7, -12...
a4= -7
d= -5
Término general: an= -7+(n-4) (-5)= -7 -5n + 20= -5n +13

29. INTERPOLACIÓN DE TÉRMINOS EN UNA PROGRESIÓN
INTERPOLACIÓN DE TÉRMINOS EN UNA PROGRESIÓN
ARITMÉTICA
ARITMÉTICA
Interpolar medios diferenciales o aritméticos entre dos números, es
construir una progresión aritmética que tenga por extremos los números
dados.
Sean los extremos a y b , y el número de medios a interpolar m .
La diferencia está dada por:

30. INTERPOLACIÓN DE TÉRMINOS EN UNA PROGRESIÓN
INTERPOLACIÓN DE TÉRMINOS EN UNA PROGRESIÓN
ARITMÉTICA
ARITMÉTICA
Interpolar tres medios aritméticos entre 8 y -12 .
a: 8
b: -12
Utilizando la fórmula obtenemos: -5
Este valor será restado al primer término y así sucesivamente el segundo:
8-5= 3
3-5= -2
-2-5= -7
Interpolar tres medios aritméticos
8, 3, -2, -7, -12

31. SUMA DE N TÉRMINOS CONSECUTIVOS DE UNA PROGRESIÓN
SUMA DE N TÉRMINOS CONSECUTIVOS DE UNA PROGRESIÓN
ARITMÉTICA
ARITMÉTICA
Calcular la suma de los primeros 5 términos de la progresión: 8, 3, -2, -7, -12...
S5= - 10

32. TÉRMINOS EQUIDISTANTES DE UNA PROGRESIÓN ARITMÉTICA
TÉRMINOS EQUIDISTANTES DE UNA PROGRESIÓN ARITMÉTICA
Sean ai y aj dos términos equidistantes de los extremos, se cumple que la suma
de términos equidistantes es igual a la suma de los extremos.
Ejemplo:
8, 3, -2, -7, -12...
3+ (-7)= (-2)+(-2)= 8+(-12)
-4 = -4 = -4

33. REFERENCES
REFERENCES
The History of Math
Algebra: First Edition
By Olivia Wilson
By Claudia Alves

34. THANK
THANK
YOU!
YOU!