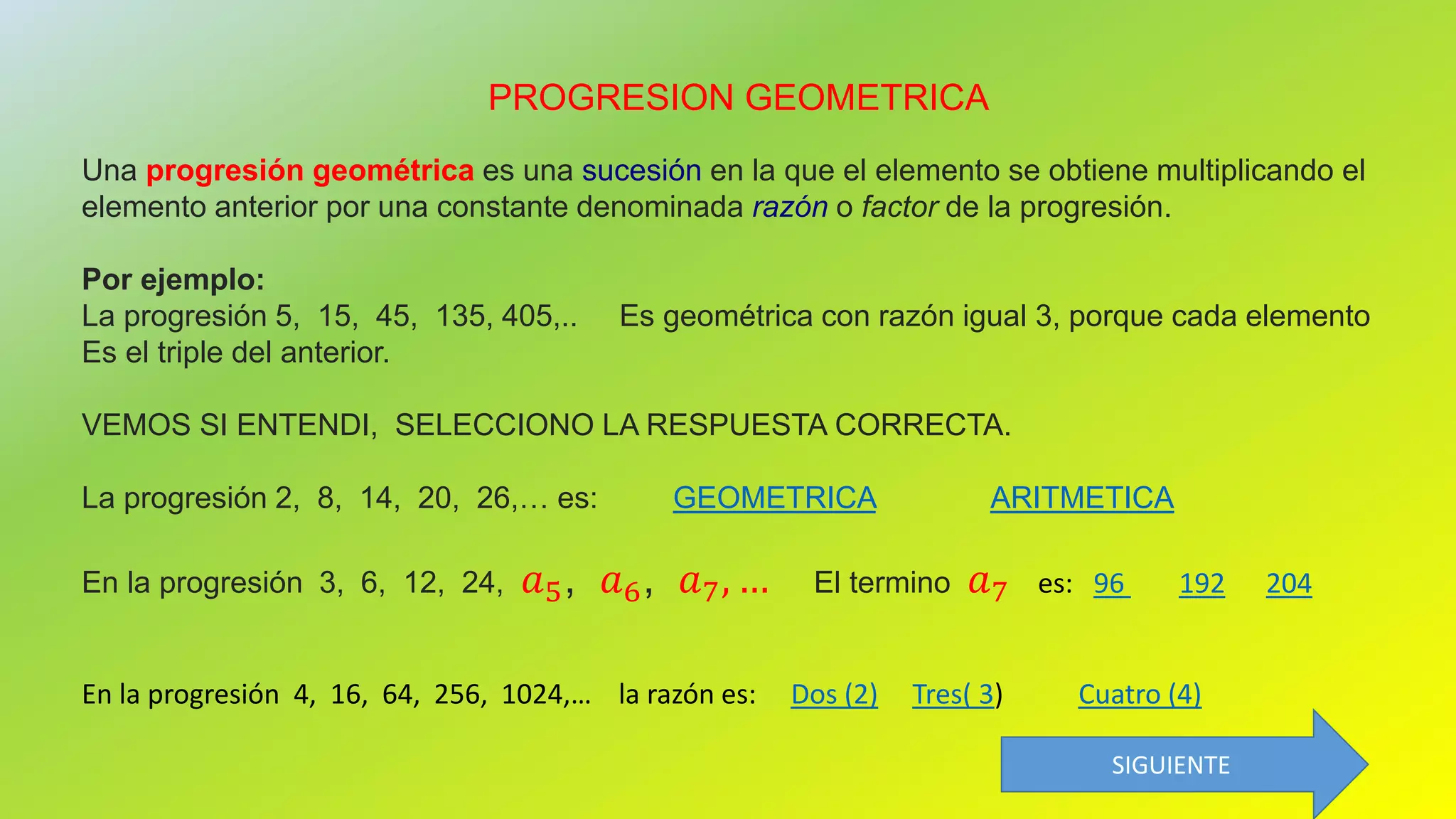
El documento presenta un curso sobre sucesiones y progresiones aritméticas y geométricas, abordando su definición, características y ejemplos prácticos. Se enseñan las fórmulas para determinar términos generales y se discuten sucesiones recurrentes como la de Fibonacci. Además, se incluyen ejercicios para practicar la identificación y cálculo de términos en sucesiones y la suma de términos en progresiones aritméticas y geométricas.

1. INSTITUCION EDUCATIVA LA INMACULADA
TIERRALTA – CORDOBA
CURSO: ALGEBRA DE NOVENO
TEMA: SUCESIONES, PROGRESIONES ARITMETICAS Y GEOMETRICAS.
OBJETIVO: IDENTIFICAR LAS SUCESIONES, PROGRESIONES ARITMETICAS Y GEOMETRICAS, ASI COMO
HALLAR TERMINOS DESCONOCIDOS EN CADA UNA DE ELLAS.
DOCENTE: OMAR MORA DIAZ
2015

2. SUSECIONES NÚMERICAS
Una sucesión es un conjunto ordenado de números reales siguiendo una regla:
a1 , a2 , a3 , a3 , a4 , a5,…
Cada elemento de la sucesión se denomina término, el subíndice es el lugar que
ocupa en la sucesión.
El primer término es a1, el segundo a2, el tercer termino es a3 …
Ejemplo: En la sucesión de los números pares: 2, 4, 6, 8, 10, 12, 14, 16,18,20,…
El primer termino a1 = 2
El segundo termino a2 = 4
El tercer termino a3 = 6
El cuarto termino a4 = 8
El quinto termino a5 = 10

3. SUCESIONES FINITAS Y SUCESIONES INFINITAS
Una sucesión es finita si contiene limitado el número de términos , y es infinita si el
número de término es ilimitado.
SUCESION
INFINITA
CARACTERISTICAS EJEMPLOS
Creciente Cualquier término de la sucesión es mayor que
el término inmediatamente anterior.
2, 4, 6, 8, 10,…
Decreciente Cualquier término de la sucesión es menor que
el término inmediatamente anterior.
5, 3, 1, -1, -3, -5,…
Oscilante Loa signos de los términos de la sucesión son
alternados. La sucesión no es creciente ni
decreciente.
3, -6, 9, -12, 15, -18,…
Constante Todos los términos de la sucesión tienen el
mismo valor.
5, 5, 5, 5, 5,…

4. TÉRMINO GENERAL DE UNA SUCESIÓN.
Representa un término cualquiera de la sucesión, el dominio es el conjunto de los
números enteros positivos.
En las sucesiones que siguen una ley de formación, la fórmula del término general,
an, permite determinar cualquier término de la sucesión.
Ejemplos:
En la sucesión de los números pares: 2, 4, 6, 8, 10, 12,…
El término general an= 2n
Observa:
a1 = 2(1) = 2
a2 = 2(2) = 4
a3 = 2(3) = 6
a4 = 2(4) = 8
a5 = 2(5) = 10
a6 = 2(6) = 12
HALLAR LOS PRIMEROS 5 TERMINOS DE LAS
SIGUIENTES SUSECIONES
DE NUMEROS REALES
1. an = 2n + 1 4. an = n2
2. an = n - 5 5. an = (- 2)n
3. an = 2n + 1 6. an = 2n + 1

5. PRACTIQUEMOS UN POCO.
Selecciono el término que corresponde al signo de interrogación.
1. 1, 3, 6, 9, 12, 15, ? R/
2. 1, 2, 4, 7, 11, 16, 22, ? R/
3. 1, 2, 4, 8, 16, 32, ? R/
4. 1, 1, 2, 3, 5, 8, 13, ? R/
5. ?, 3, 1, -1, -3, -5, -7 R/
21191817
31 30 28 29
- 6
811286472
29232124
7 - 5 5
siguiente

6. TÉRMINO GENERAL DE UNA SUCESIÓN ( an )
El término general representa un término cualquiera de la sucesión.
En las sucesiones que siguen una ley de formación, la fórmula del término general, an ,
permite determinar cualquier término de la sucesión.
EJEMPLOS:
En la sucesión de los números pares: 2, 4, 6, 8, 10, 12,… el término general an = 2n
En la sucesión: 1, 4, 9, 16, 25, … El término general an = n2
En la sucesión de los números impares: 1, 3, 5, 7, 9, 11, 13, 14, 16,… el
Término general: an = 2n - 1

7. VEAMOS QUE TANTO APRENDÍ.
𝑎 𝑛 = 5𝑛 − 23, 8, 13, 18,…
-2, -1, 0, 1, 5, 6,… 𝑎 𝑛 = 𝑛 − 3
9, 4, 1, 0, 1, 4, 9, 16,… 𝑎 𝑛 = (𝑛 − 4)2
2, 4, 8, 16, 32,…
Voy a seleccionar de las cuatro opciones el término general correspondiente a
cada sucesión.
𝑎 𝑛 = 2 𝑛
6, 8, 10, 12, 14,… 𝑎 𝑛 = 2𝑛 + 4
- 3, 9, - 27, 81, - 243,… 𝑎 𝑛 = (−3) 𝑛
𝑎 𝑛 = 𝑛 − 3𝑎 𝑛 = 𝑛 − 4𝑎 𝑛 = 2𝑛 − 3
𝑎 𝑛 = 𝑛 + 3𝑎 𝑛 = (𝑛 − 4)2 𝑎 𝑛 = (𝑛 + 4)2
𝑎 𝑛 = (𝑛 + 4)2𝑎 𝑛 = 2𝑛 − 3𝑎 𝑛 = 𝑛 − 3
𝑎 𝑛 = 2 −𝑛
𝑎 𝑛 = (𝑛 − 4)2
𝑎 𝑛 = (4)2𝑛
𝑎 𝑛 = 5𝑛 − 2 𝑎 𝑛 = 5𝑛 + 2 𝑎 𝑛 = 5𝑛
𝑎 𝑛 = 2.5 𝑛−1
𝑎 𝑛 = (−1) 𝑛(2n) 𝑎 𝑛 = 3. (2) 𝑛−1
siguiente

8. Sucesiones recurrentes.
Los términos de la sucesión se obtienen a partir de los anteriores.
Ejemplo. La sucesión de Fibonacci. 1, 1, 2, 3, 5, 8, 13, 21,…
¿Cuál es el sexto término? R/ 8
¿Cuál es el noveno término? R/ 34
¿Cuál es el decimo primero? 80 90 89 103 R/
Cada término es la suma de los dos anteriores. 𝑎 𝑛 = 𝑎 𝑛−1 + 𝑎 𝑛−2
La sucesión cambia si se modifican los dos primeros términos.
Calcula los 9 primeros términos de una sucesión con la misma ley de formación con
a1 = 1 y a2 = 3
-----, ------, ------, ------, ------, -------, ------, ------, ------ R/
VIDEO,
SUCESION DE
FIBONACCI
SUCESION DE
FIBONACCI EN
LA
NATURALEZA
Término general sucesión de Fibonacci.

9. POGRESIONES ARITMETICAS.
En matemáticas, una progresión aritmética es una sucesión de números tales que
la diferencia de dos términos sucesivos cualesquiera de la secuencia es una constante,
cantidad llamada diferencia de la progresión o simplemente diferencia o incluso
"distancia".
Por ejemplo, la sucesión matemática: 3, 5, 7, 9, 11 ... es una progresión aritmética de
constante 2. porque 5 – 3 = 2, 7 – 5 = 2, 9 – 5 = 2.
En la sucesión 5, 10, 15, 20, 25, 30,… La deferencia de dos términos consecutivos es 5
En la sucesión 1, 4, 7, 10, 16, 16, 19,… La diferencia de dos términos consecutivos es 3
En la sucesión 12, 8, 4, 0, - 4, - 8, - 12,… La diferencia entre dos términos es 4

10. TERMINO GENERAL DE UNA PROGRESION ARITMETICAS
El término general de una progresión aritmética es aquel en el que se obtiene
cualquier término restándole la diferencia al término siguiente.
El término de una progresión aritmética es la expresión que nos da cualquiera
de sus términos, conocidos alguno de ellos y la diferencia de la progresión.
La fórmula del término general de una progresión aritmética es:
𝑎 𝑛 = 𝑎1 + 𝑛 − 1 . 𝑑 Donde: n = término deseado, d = la diferencia,
𝑎1 = 𝑝𝑟𝑖𝑚𝑒𝑟 𝑡é𝑟𝑚𝑖𝑛𝑜 𝑑𝑒 𝑙𝑎 𝑝𝑟𝑜𝑔𝑟𝑒𝑠𝑖ó𝑛.
Por ejemplo:
En la progresión 3, 8, 13, 18, 23,… el Noveno término 𝑎9 = 43
Ya que d= 13 – 8 = 5, 𝑎1 = 3, n= 9 Entonces 𝑎9 = 3 + 9 − 1 . 5 = 3 + 8. 5 = 43
Luego. 3, 8, 13, 18, 23,___, ___, ___, 43,…
VIDEO DE EJERCICIOS

11. SUMA DE TODOS LOS TERMINOS DE UNA PROGRESION ARITMETICA
La suma de los términos en un segmento inicial de una sucesión aritmética se
conoce a veces como serie aritmética.
Existe una fórmula para las series aritméticas. La suma de los n primeros valores
de una sucesión finita viene dada por la fórmula:
Donde n es el número de término que se suman, 𝑎1 es el
primer término, 𝑎 𝑛 es el n - ecimo o último término a sumar.
Por ejemplo.
En la progresión. 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21,… La suma de los
primeros seis términos es: 𝑆6= 1+3+5+7+9+11= 36
Aplicando la formula, se tiene.
𝑆 𝑛 =
𝑎1 + 𝑎 𝑛 . 𝑛
2
𝑆6 =
1+11 .6
2
=
12 .6
2
= 36
VIDEOS DE EJERCICIOS

12. PROGRESION GEOMETRICA
Una progresión geométrica es una sucesión en la que el elemento se obtiene multiplicando el
elemento anterior por una constante denominada razón o factor de la progresión.
Por ejemplo:
La progresión 5, 15, 45, 135, 405,.. Es geométrica con razón igual 3, porque cada elemento
Es el triple del anterior.
VEMOS SI ENTENDI, SELECCIONO LA RESPUESTA CORRECTA.
La progresión 2, 8, 14, 20, 26,… es: GEOMETRICA ARITMETICA
En la progresión 3, 6, 12, 24, 𝑎5, 𝑎6, 𝑎7, … El termino 𝑎7 es: 96 192 204
En la progresión 4, 16, 64, 256, 1024,… la razón es: Dos (2) Tres( 3) Cuatro (4)
SIGUIENTE

13. TERMINO GENERAL DE UNA PROGRESION GEOMETRICA.
El término general de una progresión aritmética es aquel en el que se obtiene cualquier
término restándole la diferencia al término siguiente.
El término de una progresión aritmética es la expresión que nos da cualquiera de
sus términos, conocidos alguno de ellos y la diferencia de la progresión.
La fórmula del término general de una progresión Geométrica es:
an = a1 · rn-1
Donde: n = término que se quiere buscar, r = la razón entre dos términos consecutivos,
𝑎1 = 𝑝𝑟𝑖𝑚𝑒𝑟 𝑡é𝑟𝑚𝑖𝑛𝑜 𝑑𝑒 𝑙𝑎 𝑝𝑟𝑜𝑔𝑟𝑒𝑠𝑖ó𝑛.
Por ejemplo:
En la progresión 3, 6, 12, 24, 48,… el Décimo termino 𝑎10 = 43
Ya que r = 12 / 6 = 48/24 = 2, 𝑎1 = 3, n= 10 Entonces a10 = 3 · 210-1
a10 = 3 · 29 = 1536
Luego. 3, 6, 12, 24, 48,___, ___, ___, ____, 1536

14. VEAMOS QUE TANTO ENTENDI DE PROGRESIONES GEOMETRICAS.
De las cuatro opciones selecciono la correcta.
1. La progresión 2, 8, 32, 128,… es: Aritméticas geométrica oscilante constante
2. La progresión 12, 10, 8, 6, 4,… es: Aritméticas geométrica oscilante constante
3. La razón de la progresión 3, 18, 108, 648, 3888,… es: 2 4 5 6
4. Los primeros 4 términos de 𝑎 𝑛= 𝑎1. 𝑟 𝑛−1
es: 7, 112, 468, 1762 7, 112, 448, 1792
5. Los primeros 4 términos de 𝑎 𝑛 = 80.
1
2
𝑛−1
, es: 80, 40, 20, 10 80, 40, 20, 15
6. El decimo (𝑎10 ) termino de 𝑎 𝑛 = 6. 2 𝑛−1 es: 3072 3270 3027
VIDEO EJEMPLO 1 VIDEO EJEMPLO 2

15. SUMATORIA DE LOS TERMINOS DE UNA PROGRESION GEOMETRICA
La suma de los términos en un segmento inicial de una sucesión geométrica se conoce a
veces como serie geométrica.
Existe una fórmula para las series geométrica. La suma (𝑠 𝑛 ) de los primeros valores
de una sucesión finita viene dada por la fórmula: 𝑠 𝑛 =
𝑎1.(𝑟 𝑛−1)
𝑟−1
, Donde: n = son
los termino que se quieren sumar, r = la razón entre dos términos consecutivos,
𝑎1 = 𝑝𝑟𝑖𝑚𝑒𝑟 𝑡é𝑟𝑚𝑖𝑛𝑜 𝑑𝑒 𝑙𝑎 𝑝𝑟𝑜𝑔𝑟𝑒𝑠𝑖ó𝑛.
Ejemplo:
En la progresión 3, 6, 12, 24, 48, 96,…. La suma de los primeros 5 términos 𝑠5 es:
𝑠5 =
𝑎1.(𝑟 𝑛−1)
𝑟−1
=
3 (25−1)
2−1
=
3 (32−1)
2−1
=
3 (31)
1
= 93
VIDEO EJEMPLO 1

16. ES HORA DE AFIANZAR MIS CONOCIMIENTOS EN SUCESIONES Y PROGRESIONES.
DESCARGAR ARCHIVO
TALLER EN CASA.
FIN