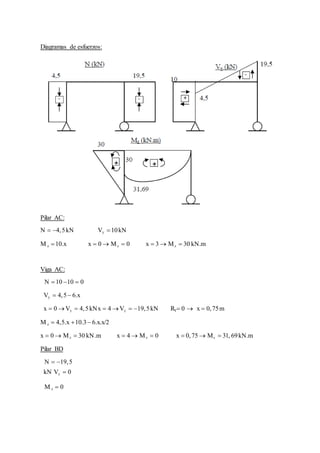
Este documento describe las vigas como elementos estructurales que soportan y transmiten cargas. Explica que las vigas trabajan principalmente a flexión y tienen diferentes tipos de apoyo y cargas que actúan sobre ellas. También describe diferentes clases de vigas y métodos para calcular las reacciones en los apoyos.

1. LAS VIGAS COMO ELEMENTOS ESTRUCTURALES
1. Viga
Es el elemento arquitectónico rígido, generalmente horizontal, proyectado para
soportar y transmitir las cargas transversales a que está sometido hacia elementos
de apoyo, que trabaja principalmente a flexión. En las vigas la longitud predomina
sobre las otras dos dimensiones. Las vigas son elementos constructivos lineales
que constituyen el esqueleto de las edificaciones arquitectónicas. Regulan la
tensión que tendrá la construcción y soportan el resto de los materiales
empleados para la edificación, las tensiones máximas se hallan en la parte
inferior y en la superior, por lo que en esos sectores es en donde la viga debe
ser más fuerte, para no dejar lugar a las torsiones.
2. Los tres tipos de apoyo más comunes y sus representaciones esquemáticas.
2.1. Apoyo móvil o de rodillo:
Éste permite el desplazamiento a lo largo del eje longitudinal
de la viga y el giro de ésta; el desplazamiento transversal es
impedido mediante una reacción en ese sentido.
2.2. Apoyofijoopasador:
Este tipo de apoyo permite el giro de la viga, pero impide el
desplazamientoencualquierdirecciónmediante unareacciónque se
puede dividirenunacomponente a lolargo del eje longitudinal de la
viga y otra a lo largo del eje transversal. Para determinar estas dos
componentesesnecesariohacerusode dosecuacionesde laestática
2.3. Empotramiento:
Este tipo de apoyo impide el desplazamiento a lo largo de los ejes y
el giro de la viga mediante unareacciónque se puede dividirenuna
componente longitudinal, otra transversal y una reacción de
momento.
3. Tipos de cargas en las vigas.
Una viga está sometida a dos grupos de fuerzas determinadas concentradas o
puntuales y distribuidas. El primer grupo está formado por fuerzas actuando en un

2. punto definido. Como por ejemplo. Una fuerza aplicada o un momento aplicado y
están expresadas en unidades de fuerza o momentos
En cuanto al segundo plano la carga distribuida es aquella que actúa sobre una
longitud de la viga. La magnitud de la carga distribuida puede ser constante por
unidad de longitud o variable y se expresa en unidades de longitud (N/m. Lb/pie.
Kg/m) la magnitud de la fuerza originada por esta carga es igual al área de la forma
generada por la carga y se ubica en el centroide de la mencionada forma.
3.1. Carga de servicio.
Carga concentrada que se aplica en el nudo de una cercha. También
llamada carga de trabajo, carga de uso.
3.2. Carga puntual.
Carga que actúa sobre un área
muy pequeña o un punto muy
concreto de una estructura.
También llamada carga
concentrada.
3.3. Carga variable.
Carga externa movible sobre una estructura
que incluye el peso de la misma junto con el
mobiliario, equipamiento, personas, etc.
Que actúa verticalmente, por tanto no
incluye la carga eólica, también llamada
carga viva.
3.4. Carga distribuida.
Carga que se aplica a toda la longitud de un elemento estructural o a una
parte de éste. También llamada carga repartida.

3. 3.5. Carga muerta.
Carga vertical aplicada sobre una estructura que incluye el peso de la
misma estructura más la de los elementos permanentes
3.6. Carga de impacto.
Efecto dinámico que sobre una estructura, móvil o estática, tiene una
carga aplicada de corta duración debido a su movimiento.
4. Clases de vigas.
4.1. Viga simplemente apoyada con voladizo.
Es la viga que esta soportada en apoyos simples en los extremos y que
permiten el libre movimiento de sus extremos.
El voladizo es un elemento estructural rígido, que está apoyado solo por un
lado a un elemento, del que sobre sale. También se pueden construir
voladizos con celosías o forjados, cuando se somete a una carga el
voladizo la transmite al apoyo en el que está sujeto en forma e momento.
4.2. Viga simplemente apoyada sin voladizo

4. 4.3. Viga en voladizo
4.4. Viga doblemente empotrada
4.5. Viga empotrada apoyada
4.6. Viga continua

5. 5. Calculo de reacciones.
5.1. Método de las secciones.
Se usa para determinar las cargas que actúan dentro de un cuerpo, este método
se basa en el principio de que si un cuerpo está en equilibrio, entonces cualquier
parte del cuerpo está también en equilibrio.
El método de las secciones puede usarse también para “cortar” o seccionar los
miembros de toda una armadura. Si la sección pasa por la armadura y se traza el
diagrama de cuerpo libre de cualquiera de sus dos partes, entonces puedes aplicar
las ecuaciones de equilibrio o esa parte para determinar las fuerzas del miembro
en la “sección cortada”. Como sólo tres ecuaciones independientes de equilibrio
(ƩFX = 0, ƩFY = 0, ƩM0 = 0) pueden ser aplicadas a la parte aislada de la armadura,
trata de seleccionar una sección que, en general, pase por no más de tres
miembros en que las fuerzas sean desconcentradas.
Al aplicar las ecuaciones de equilibrio, debes considerar maneras de escribir las
ecuaciones en forma tal que den una solución directa para cada una de las
incógnitas, en vez de tener que resolver ecuaciones simultáneas.
5.2. Método de los nodos.
5.3. Método por condición de equilibrio.
Para determinar las reacciones de una viga mediante un análisis estático
en dos dimensiones se debe proceder de la siguiente manera:
 Determinar el diagrama de cuerpo libre. En el cual se aísla la viga
de sus apoyos, sustituyéndolos por las fuerzas que se genera en los
apoyos o reacciones, así como las fuerzas externas aplicadas en la
viga.
 Determinar si el cuerpo es estáticamente determinado. Si el número
de reacciones es menor de 3: por otra parte si el número es mayor
que 3 la estructura es indeterminada y el análisis estático finaliza.
Si la estructura es isostática se verifica la estabilidad, de no ser
estables, el análisis igualmente finaliza.
 Se determina las reacciones usando la ecuación 1, e manera que
en cada ecuación exista solo una incógnita o reacción. El signo
positivo de la respuesta para la magnitud de la fuerza indica que el
sentido supuesto en el diagrama de cuerpo libre era correcto, el
signo negativo indica que el sentido correcto e la reacción es
contrario al supuesto inicialmente.
 Se debe determinar las tres reacciones usando tres ecuaciones de
equilibrio.

6.  Los resultados deben ser verificados con las ecuaciones que hayan
sido utilizados.
EJEMPLOS
1. Encuentre las reacciones de los apoyos de la viga que se
muestran en la figura.
SOLUCION.
De acuerdo a los apoyos que se pueden observar en el esquema se
generan las reacciones que se observan en la figura siguiente:
Ahora aplicando las ecuaciones de la estática se tiene.
∑Fx = 0 HA ═ 0
∑ Fy = 0 VA+VB – 100 – 160
VA+VB = 260
∑MA = 0 -200 – 100*0,2 – 160*0,3 + VB * 0,4 = 0
VB = 670N
Ahora como Ahora, como:
V 𝐴 + V 𝐵 = 260 N v 𝐴 = 260 − 670 = −410N
El signo negativo en VA indica que tiene el sentido contrario al
indicado en la figura.
A
B
0,1m 0,1m 0,1m 0,1m
200N*m
100N 160N
100N
200N*m
160N
A
B
HA
VA
VB

7. 2. En una viga empotrada en la pared encuentre las reacciones de
los apoyos y el momento de la viga empotrada que se muestran
en la figura.
SOLUCION:
∑Fx = 0 Bx═ 0
∑ Fy = 0 -50+15+By=0
By= 35KN
∑MB = 0 (-15)(2.5)+10+(30)(1)+(20)(0.5)+M = 0
M = -12.5 KN.m
3. En una barra empotrada en la pared de longitud 100 cm, se
cuelga de un cuerpo de masa de 2 Kg. Encuentre las fuerzas de
apoyo y cuál será el momento respecto del punto de apoyo de la
pared.
0,5m 0,5m0,5m1m
15KN
20KN30KN
A
C
D E B
0,5m 0,5m0,5m1m
20KN30KN
A
C
D E B
Bx
By
15KN
M
F
2kg
100 cm

8. SOLUCION:
F= m*g= (2Kg) (9,8m/s )= 19.6 N
∑Fx = 0 Ax═ 0
∑ Fy = 0 -19,6+Ay=0
Ay= 19,6KN
∑MA= 0 (-19,6N)(1m)+M= 0
M = 19,6 N.m
4. Representar los diagramas de fuerzas cortantes y de momento
flectores de la viga de la figura.
Cálculo de reacciones en los apoyos: Ecuaciones de equilibrio
F = 0 RA + RB =15.2+20+8 (1) resolviendo: RA =23kN
MA = 0 RB .4=15.2.1+20.3+8.5 (2) RB =35kN
B
F
2kg
100 cmA
M
Ax
Ay
2

9. Diagrama de esfuerzos:
0-x-2
Vy = 23-15x x=0 Vy = 23kN x=2 V y =-7kN
Vy =0 23-15.x=0 x=1.53m

10. 5. Representarlosdiagramasde fuerzascortantesyde momentosflectoresde
la vigade la figura
Cálculo de las reacciones:Ecuaciones de equilibrio:
Diagrama de esfuerzos:
Por semejanzas de triángulos:

11. 6. Representarlosdiagramasde fuerzascortantesyde momentosflectoresde la
vigade lafigurasometidaalas cargas verticalesyhorizontalesindicadas.
Calculode reacciones:Ecuacionesde equilibrio:
Diagrama de esfuerzos:
0 x1
Vy 7,5kN Vz 2kN
M z 7,5.x x 0 M z 0
M y 2.x x 0 M y 0

12. 1x 3
Vy 7,510 2,5kN
Vz 2kN
M z 7,5.x10.( x 1) x 1Mz 7,5kN.m x 3Mz 2,5kN.m
M y 2.x x 1My 2kN.m x 3M y 6kN.m
3x 4
Vy 7,510 2,5kN
Vz 28 6k
M z 7,5.x10.( x 1) x 3Mz 2,50kN.m x 4 Mz 0
M y 2.x 8.(x 3) x 3 M y 6kN.m x 4 M y 0
7. Representar los diagramas de solicitaciones de la estructura de nudos
rígidos de la figura
Cálculo de reacciones:Ecuaciones de equilibrio:
FH 0 H A 10 kN
FV 0 VA VB 6.4 Resolviendo: VA 4,5kN
M A 0 VB.4 10.3 6.4.2 VB 19,5kN

13. Diagramas de esfuerzos:
Pilar AC:
N 4,5kN Vy 10kN
M z 10.x x 0 Mz 0 x 3 Mz 30 kN.m
Viga AC:
N 10 10 0
Vy 4,56.x
x 0 Vy 4,5kNx 4 Vy 19,5kN RY0  x 0,75m
M z 4,5.x 10.36.x.x/2
x 0 Mz 30 kN.m x 4 Mz 0 x 0,75 Mz 31, 69kN.m
Pilar BD
N 19,5
kN Vy 0
M z 0

14. 8. Representarlosdiagramasde solicitaciones de lavigade lafigura.
Solución:

15. Calculo de reacciones:
0x 1: Vy Vz Mz 0 M y 8 kN.m
1x3: Vy 65,69.(3x).(x 1) x 1).189.(3x)
x 1Vy 65,6 kN x 3Vy 47,6 kN
Vz 14,8 kN
Mz 65,6.(x 1)9.(3x).(x1).(x1)/21/2.(x 1).189.(3x).2/3.(x1)10
x 1Mz 10 kN.m x 3Mz 97,2 kN.m
M y 814,8.(x 1)
x 1My 8 kN.m x 3My 21,6kN.m
3x 6: V y 65,6.18.25020.(x 3)
x 3 Vy 2,4kN x 6 Vy 62,4kN
Vz 14,8 22 7,2 kN
M z 65,6.(x 1) .18.2.(x 1)1050.(x 3) 20.(x 3).(x 3)/2
x 3 Mz 97,2 kN.m x 6 Mz 0 kN.m
M y 814,8.(x 1)22.(x 3)
x 3 My 21,6kN.m x 6 M y 0 kN.m

16. 9. Encuentre las reacciones de los apoyos de la viga que se
muestra en la figura:
Solución:
De acuerdoa losapoyos que se puedenobservarenel esquemase generanlasreacciones que
se observan enlafigurasiguiente:
Ahora, aplicandolasecuaciones de laestáticase tiene:
Fx=0→ HA=0
Fy=0→ V A+ V B –100–160=0
V A+ V B = 260 N
MA=0→–200–100.0,2–160.0,3+ V B .0.4=0
V B = 670 N
Ahora, como: V A+ V B = 260 N→ V A= 260 –670= –410 N
El signo negativo en V A indica que tiene sentido contrario al indicado en la figura.

17. 10. Determine las reacciones en A y B para la viga de la figura
Solución:
Usando lasecuacionesde laestáticase tiene:
Fx=0→ HA–5.Cos53– VB .Cos45=0
Fy=0→ VA +V B .Sen45–5.Sen53=0
VA =5.Sen53– V B .Sen45
MA=0→–5.Sen53.3+ V B .Sen45.12=0
Luego:
VA =5.Sen53–1, 41.Sen45
VA =3 N
HA=5.Cos53+3.Cos45
HA=5, 13 N